Урок математики по теме: "Приращение аргумента и приращение функции"

Гонодинская СОШ

 Алгебра

Урок «Приращение аргумента и приращение функции»

Цели :

образовательные: сформировать понятия приращения функции и приращения аргумента, показать применение данных понятий при решении задач.

развивающие: развитие вычислительных навыков, умений логически и аргументированно рассуждать, обобщать и абстрагировать.

воспитательные: воспитание познавательного интереса к предмету.

          Тип урока: изучение нового материала.

Оборудование: карточки, задания.

Ход урока

1.Организационный момент (проверить готовность к уроку).

2. Актуализация темы

         Дайте определение функции?

         Как называют переменную х?

         Как называют переменную у?

        3.Изучение нового материала.

Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)−f(x0) называют приращением функции.

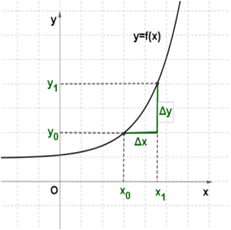
Приращение аргумента обозначают Δx (читают: дельта икс; Δ — прописная буква греческого алфавита "дельта"; Приращение функции обозначают Δy или Δf.

Итак, x1−x0=Δx, значит, x1=x0+Δx.

f(x1)−f(x0)=Δy, значит, Δy=f(x0+Δx)−f(x0).

Нельзя истолковывать термин "приращение" как "прирост".

Функция y=f(x) непрерывна в точке x=a, если в этой точке выполняется следующее условие: если Δx→0, то Δy→0.

Например задание. Вычислите приращение функции f(x) в произвольной точке, если: а) f(x)=2x²+3x-5;    б) f(x)=sin2x

Предлагается решить задание трех уровней сложности:

Уровень А.

1). f(x)=3x-8;             2). f(x)=2-x²;             3). f(x)=x³+4.

Уровень В.

1). f(x)=;             2). f(x)=;                3). f(x)=7^x.

Уровень С.

1). f(x)=sin;           2). f(x)=1-cos x;         3). f(x)=tg3x.

Итог урока . Что нового узнал на уроке?

                       Что у меня получилось, а что не получилось?

                        Выставление оценок.

Домашнее задание :выучить определения ,решить  №780

Урок «Производная функции.»

Цели урока:

-образовательная: вырабатывать навыки нахождения производной по определению и формулам , применять их при решении конкретных задач;

развивающая: развивать логическое мышление, внимание, интерес к предмету, стремление глубже усвоить предмет;

воспитательная: воспитывать интерес к математике и физике, воспитывать чувство ответственности, организованности, настойчивости и упорства в достижении цели.

Тип урока : изучение нового материала

Оборудование : карточки с заданием, формулы .

Ход урока

1.Организационный момент (проверка готовности к уроку)

2. Запишем основные формулы нахождения производных

3. Изучение нового материала

Задание. Вычислите по определению  производную функции f(x) в точке х₀=2, если: a) f(x)=3x²-5x+1;    б) f(x)=

Предлагается решить задание трех уровней сложности:

Уровень А.

1). f(x)=2x+3;             2). f(x)=3x² - 2;             3). f(x)=5x – x².

Используя формулы дифференцирования:

1)  f(x)= ;   2) f(x)=

Уровень В.

1). f(x)=cos x;             2). f(x)=;

       Используя формулы дифференцирования

1) f(x)=  2)

Уровень С.

1). f(x)=;             2). f(x)=sin 2x;              3). f(x)=.

Используя формулы дифференцирования

1)   2) f(x)=

Итог урока . Что нового узнал на уроке?

                        Что у меня получилось, а что не получилось?

                        Выставление оценок.

Домашнее задание : выучить правило нахождения производных по определению и формулы, решить  №839