Урок на тему: Арифметическая и геометрическая прогрессии

         Тема урока: «Арифметическая и геометрическая прогрессии»

         Цель урока:

обобщение и систематизация  тем  «Арифметическая прогрессия» и «Геометрическая прогрессия»;

         Задачи  урока:

- обобщить и систематизировать теоретические знания  учащихся;

- отработать  умения и навыки применения формул  n –го члена прогрессии, суммы n первых членов прогрессии;

- развивать  навыки работы с дополнительной литературой, с историческим материалом;

- развивать познавательную активность учащихся, память, воображение, внимание, наблюдательность;

- воспитание эстетические качества и умение общаться;

- формировать интерес к математике, положительный  мотив учения;

- подготовка к контрольной работе.

         Оборудование:

 мультимедиа проектор,

 раздаточный материал,

           учебное электронное пособие «Математика 5-11»

Ход урока.

I.                  Организационный момент.

- Приветствие учителя. Создание доброжелательной атмосферы в классе.
-  Тему сегодняшнего урока мы узнаем, разгадав кроссворд (Работа в парах, с последующей проверкой. Задания лежат на парте).  (Приложение 1)

-  Сообщение темы, цели  и задач урока. (Слайды)

II.               Актуализация знаний.

Рефлексия: Выбери из предложенных рисунков тот, который соответствует твоему настроению на начало урока и отметь его.

Учащиеся работают с листами-опросниками, проставляя «+» или «-».

В конце урока  оценивают себя, выставляя оценку.

1. Составление кластера (доска разделена на 2 части)- работают по цепочке, записывая соответствующие формулы

Обобщение: что знают, не знают, трудности.

Что должны повторить, чтобы справиться с трудностями?

Кластер (Слайд)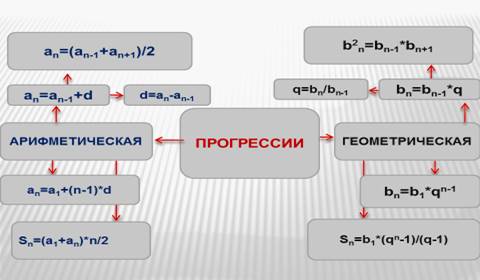

III.           Выполнение упражнений.

Работа в тетрадях

1. Определить вид прогрессии и продолжить числовой ряд – с проверкой (Слайд )

2. Задачи на применение формул арифметической и геометрической прогрессии (Слайд)

Проверка решения на доске, затем проверка на компьютере.

3. Работа в парах с последующей взаимопроверкой

3. Тест (с последующей взаимопроверкой) (Подготовка к ГИА)

Задания теста у каждого ученика (Приложение 2)

IV.  Итог урока.

Рефлексия:

Что для вас было  интересного на уроке?

Какие задания вам показались трудными?

Выбери из предложенных рисунков тот, который соответствует твоему настроению после пройденного урока и отметь его.

Поставь себе оценку за урок. (Возвращение к листу-опроснику)

VI. Домашнее задание

ž 1. В амфитеатре расположены 10 рядов, причем в каждом следующем ряду на 20 мест больше чем в предыдущем, а в последнем ряду 280 мест. Сколько человек вмещает амфитеатр?

ž 2. В сборнике по подготовке к экзамену-240 задач. Ученик планирует начать их   решение 2 мая, а закончить 16 мая, решая  каждый день на две задачи больше, чем в предыдущий день. Сколько задач ученик запланировал решить 12 мая?

ž Доп. задание (по желанию). Составить условие задачи по теме «Арифметическая прогрессия в жизни и быту» (на отдельном листочке) и решить её.

ž Подготовка к контрольной работе.

Литература:

1. Учебное электронное пособие «Математика 5-11», Дрофа

2. Учебно-методическое пособие. Взаимосвязь теории с практикой в процессе изучения математики. Возняк Г.М., Маланюк М.П.  Киев. «Радянська школа»

3. http://festival.1september.ru (Кроссворд)

Приложение 1

1. Как называется график квадратичной функции?

2. Математическое предложение, справедливость которого доказывается.

3. Упорядоченная пара чисел, задающая положение точки на плоскости.

4. Наука, возникшая в глубокой древности в Вавилоне и Египте, а учащиеся  начинают её изучать с 7 класса.

5. Линия на плоскости, задаваемая уравнением   у=кх+b.

6. Числовой промежуток.

7. Предложение, принимаемое без доказательства.

8. Результат сложения

9. Название второй координаты на плоскости.

10. Французский математик 19 века, «отец» алгебры, юрист, разгадал шифр, применяемый испанцами в войне с французами, а нам помог в быстром
решении квадратных уравнений.  

Приложение 2

Часть I (0,5 балла )

1. Про арифметическую прогрессию (аn) известно, что а = 8, а = 12. Найдите разность арифметической прогрессии.

А) -4      Б) 4      Б) 4       Г) 3

2.Геометрическая прогрессия задана формулой

Найдите знаменатель геометрической прогрессии.

А) -3      Б) 18      В)  3       Г) 9

3. Члены арифметической прогрессии изображены (рис.1) точками на координатной плоскости. Какое из данных чисел является членом этой прогрессии?

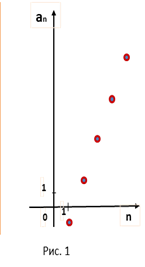
А)  -7       Б)  6     В) 12     Г)  17

4. Найдите сумму семи первых членов геометрической прогрессии 4; 8; …

А) – 254    Б) 508    В) 608     Г) - 508

 5. Последовательность аn задана формулой

 Найдите номер члена последовательности, равного 7.

А) 4        Б) -2          В)  2          Г)    -4

Часть II

Задание на 2 балла

6. В геометрической прогрессии (bn)  b = 8, b = 24.   Найдите b (для q > 0)

Задание на 3 балла

7. Сумма второго и пятого членов арифметической прогрессии равна 11. Третий её член на 6 больше первого.  Найдите второй и четвёртый члены. 

КРИТЕРИИ ОЦЕНОК