Урок обобщения и систематизации знаний по теме «Производная и ее геометрический смысл»

Предмет: алгебра и начала анализа

Класс: 11 класс

Тема: Урок обобщения и систематизации знаний по теме «Производная и ее геометрический смысл» (слайд 1)

Девиз урока:                Скажи мне, и я забуду

                                      покажи мне, и я запомню

                                      Дай действовать самому

                                      И я научусь.

                                                                      Конфуций (слайд 2)

Цели урока:

-       систематизировать знания и умения по теме «Производная»: формулы и правила дифференцирования, геометрический и физический смысл производной;

-       развивать творческую и мыслительную деятельность учащихся, способность к «видению» проблемы, формировать умения чётко и ясно излагать свои мысли;

-       воспитывать умение работать с имеющейся информацией, слушать товарищей, точно, однозначно и лаконично формулировать свои ответы (слайд 3)

Ход урока (слайд 4)

1. Организационный момент

Учитель сообщает  цель  урока и рассматривает план работы урока.

2. Фронтальная работа

Устный счет:

1. Найти производную (слайд 5)

1) Что называется производной функции  f(х) в точке х_о?

2) Укажите, для какой из функций

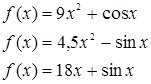
                      Функция  является производной.

                     Ответ: f(x)=4,5x² – sin x

3)– 9) Найдите производную функции: (слайд 6)

                                                              подсказка                     ответ

3)                                                 y= x⁴-x³                                       y´=4x³- 3x²

4)                            y=x⁴-1                           y´=4x³

5)                                                                               y´=

6)  у=cos²х+sin²х                                     y=1                              y´=0

7)  у=cos²х-sin²х                                      y=cos2x                       y´=-2sin2x

8)  у=(х-2)(х²+2х+4)                                y=x³-8                          y´=3x²

9)                                                     y =                          y´=

10)  Найдите скорость изменения функции  h(x)=4x³-x²    в  х_о=0

                             подсказка  v(x)=h´(x)=12х²-2х;            ответ               v(0)=0.

Фронтальную работу оценивает учитель, ученики выставляют баллы в оценочный лист.

2. Составь пару (один из вариантов)  (слайд 7)

Объяснение задания: В клетках таблицы  записаны функции. Для каждой функции найдите производную и запишите соответствие клеток. Например:,следовательно ответ:1- 9; и т.д.

Ответы: 1-9; 6-3; 11-14; 16-19; 2-4; 7-18; 12-19; 17-13; 3-5; 8-17; 4-19; 5-19; 15-16;10-20  (слайд 8)

Ученики выставляют в оценочный лист баллы, 1 балл за один правильный ответ.

3. Групповая работа

1 группа и 2 группа работают  под руководством ученика, ответственного за данную группу. 3 группа (менее подготовленная) работает под руководством учителя. У каждого учащегося 1 и 2 группы своя зачётная карточка. Все решают. На возникшие вопросы, получают консультацию у ответственного за группу или учителя. После  выполнения  работы  учитель проверяет работы у ответственных, а ответственные у членов своей группы.

А в это время 3 группа под руководством учителя работает следующим образом:

Учитель предлагает задания  (слайд 9)

Один из учеников третьей группы решает его на доске. Затем каждый ученик выполняет аналогичные задания на месте.

Задания 3 группы

В помощь ученикам 3 группы дается образец решения  (слайд 10)

Пока  ученики 3 группы выполнят  задания, учитель подводит итоги с учениками 1 и 2 группы. Наиболее сложные задания разбираются на доске.

Учащиеся проверяют решение и сверяют ответы  (слайд 11)

Руководители 1 и 2 группы выставляют баллы в оценочный лист в зависимости от выполненных заданий. Результаты выполнения работы 3 группы проверяет учитель и выставляет баллы в оценочный лист.

4. Программированный контроль

Повторив определение производной и правила нахождения производной, учащиеся проверяют свои знания с помощью программированного контроля.

У каждого ученика на столе приготовлена карточка программированного контроля. Карточки приготовлены индивидуально (по уровню сложности).

Ключом к ответу является слово, имеющее отношение  к математике. Учитель объясняет на данном примере  (слайд 12)

Образец .

Ответ: радиус.

После выполнения работы учащиеся сверяют свои ответы и выставляют баллы в оценочный лист.

Ответы: №1 - куб; №2 - луч; №3 - час; №4 - шар; №5 – знак; №6 - метр; №7 -угол; №8 - плюс; №9 - тело; №10 - конус; №11 - точка; №12 - число; №13 -минус (слайд 13)

5. Дополнительные задания

Для тех кто, выполнил своё задание, выполняют задания:

         - дружная четвёрка

Задание: Установите соответствия между функцией, записанной в строке А, её изображение в строке Б, производной функции в строке В и графиком производной в строке Г (слайд 14)

Ответы: (слайд 15)

6. Домашнее задание: 

              уч. стр.258, работа Проверь себя (слайд 16)

7. Подведение итогов урока (слайд 17)

Выставление оценок.

Примечание: все записи решения заданий выполняются в рабочих тетрадях, а баллы выставляются в оценочный лист (оценочный лист для каждой группы).

Оценочный лист

Скачано с www.znanio.ru