Класс: 8

Учебник: Алгебра 8 класс под редакцией  А. Г. Мордковича.

Тип урока: Открытие нового знания.

Тема: «Кусочно-заданная функция».

Цели:    I) для учителя цели зафиксированы в каждом этапе урока;

              II)  для ученика:

 Личностные цели:

·        Научиться ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи;

·        Научиться применять подученные знания и навыки к решению новых проблем;

·        Научиться контролировать процесс и результат своей деятельности;

Метапредметные цели:

В познавательной деятельности:

·        Развитие логического мышления и речи, умения логически обосновывать свои суждения, проводить несложные систематизации;

·        Научиться выдвигать гипотезы при решении задач, понимать необходимость их проверки;

·        Применять знания в стандартной ситуации, научиться самостоятельно выполнять задания;

·        Осуществлять перенос знаний в изменённую ситуацию, видеть задачу в контексте проблемной ситуации;

В информационно-коммуникативной деятельности:

·        Научиться вести диалог, признавать право на иное мнение;

  В рефлексивной деятельности:

·        Научиться предвидеть возможные последствия своих действий;

·        Научиться устранять причины возникновения трудностей.

Предметные цели:

·        Узнать, что такое  кусочно-заданной функция ;

·        Научиться задавать кусочно-заданную функцию аналитически по ее графику;

Ход урока

1. Самоопределение к учебной деятельности

Цель этапа:

1) включить учащихся в учебную деятельность;

2) определить содержательные рамки урока: продолжаем повторять тему числовые функции.

Организация учебного процесса на этапе 1:

У:  Чем мы занимались на предыдущих уроках?

Д:  Повторяли тему числовые функции.

У:  Сегодня мы продолжим повторять тему предыдущих уроков, а также мы должны сегодня выяснить, что нового в этой теме мы можем узнать.

2. Актуализация знаний и фиксация затруднений в деятельности

Цель этапа:

1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: вспомнить формулы числовых функций, их свойства и способы построения;

2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;

3) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний: задание кусочно-заданной функции аналитически, а так же построения ее графика.

Организация учебного процесса на этапе 2:

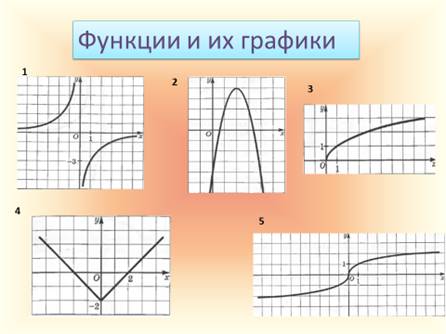
1.     Слайд 1

У: На слайде изображено пять числовых функций. Определите  их вид.

Д: 1) дробно-рациональная; 2) квадратичная; 3) иррациональная; 4) функция с модулем; 5) степенная.

У: Назовите формулы  соответствующие им.

Д: 1) ; 2)  или ; 3) ; 4) ; 5) ;

У: Давайте обсудим, какую роль выполняет каждый коэффициент в данных формулах?

Д:  Переменные «l» и «m» отвечают за сдвиг графиков данных функций влево- вправо и вверх- вниз соответственно, коэффициент «к» в первой функции определяет положение веток гиперболы: к>0 -ветви находятся в I и III четвертях, к<0 -во II и IV четвертях, а  коэффициент «а» определяет направление ветвей параболы: а>0-ветви направлены вверх, а<0 -вниз).

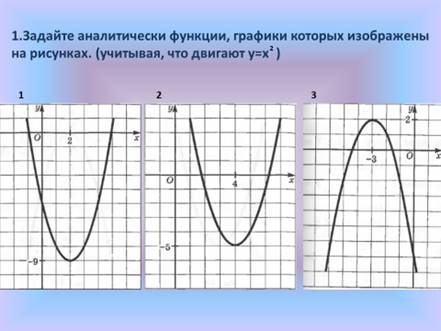
2. Слайд 2

У: Задайте аналитически функции, графики которых изображены

на рисунках. (учитывая, что двигают y=х²  ). Учитель выписывает ответы на доске.

 Д: 1) );   2);    3) ; )

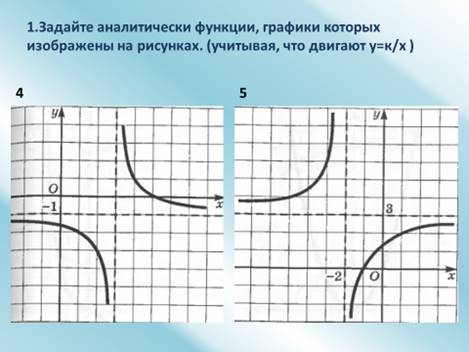
3. Слайд 3

У: Задайте аналитически функции, графики которых изображены

на рисунках. (учитывая, что двигают    ). Учитель выписывает ответы на доске.

Д:   4);   5)  .

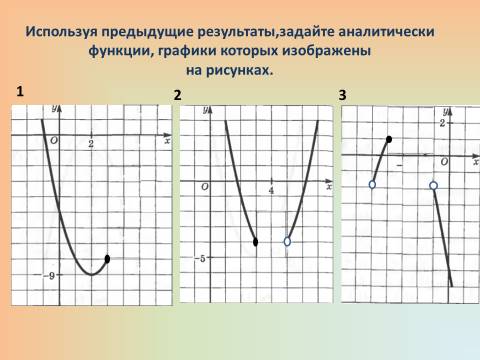
4. Слайд 4

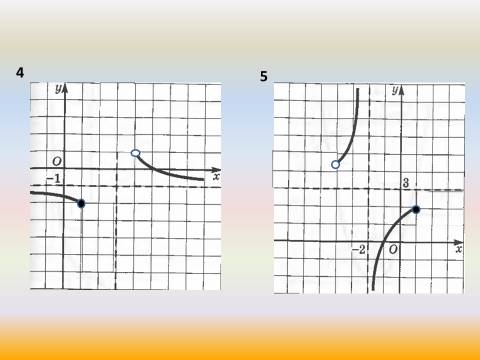
 У: Используя предыдущие результаты, задайте аналитически функции, графики которых изображены на рисунках.

3. Выявление причин затруднений и постановка цели деятельности

Цель этапа:

1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;

2) согласовать цель и тему урока.

Организация учебного процесса на этапе 3:

У: Что вызывает у вас затруднения?

Д: На экране предоставлены кусочки графиков.

У: Какова же цель нашего урока?

Д: Научиться задавать  аналитически кусочки функций.

У: Сформулируйте тему урока. (Дети пытаются самостоятельно сформулировать тему. Учитель ее уточняет. Тема: Кусочно-заданная функция.)

4. Построение проекта выхода из затруднения

Цель этапа:

1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;

2) зафиксировать новый способ действия.

Организация учебного процесса на этапе 4:

У: Давайте еще раз внимательно прочитаем задание. Какие результаты в качестве помощи просят использовать?

Д: Предыдущие, т.е. те, которые записаны на доске.

У: Может эти формулы уже являются ответом на данное задание?

Д: Нет, т.к. этими формулами задается квадратичная и рациональная функции, а на слайде изображены их кусочки.

У: Давайте обсудим,  каким промежуткам оси абсцисс соответствуют кусочки первой функций ?

Д:

У: Тогда аналитический способ задания первой функции выглядит как:

, если

У: Что нужно сделать, чтобы выполнить аналогичное задание?

Д: Записать формулу и определить, каким промежуткам оси абсцисс соответствуют кусочки данной функций.

5. Первичное закрепление во внешней речи

Цель этапа:

зафиксировать изученное учебное содержание во внешней речи.

Организация учебного процесса на этапе 5:

У: Используя полученные выводы, выполните данное задание для 2-го,3-го,4-го графиков .

      2), если  ;

      3) , если ;

      4), если .

6. Самостоятельная работа с самопроверкой по эталону

Цель этапа:

проверить своё умение применять новое учебное содержание в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.

Организация учебного процесса на этапе 6:

У: Попробуйте самостоятельно выполнить задание для 5-го графика. На закрытой части доски образец для самопроверки:

                    5)  , если .

7. Включение в систему знаний и повторение

Цель этапа:

 тренировать навыки использования нового содержания совместно с ранее изученным.

Организация учебного процесса на этапе 7:

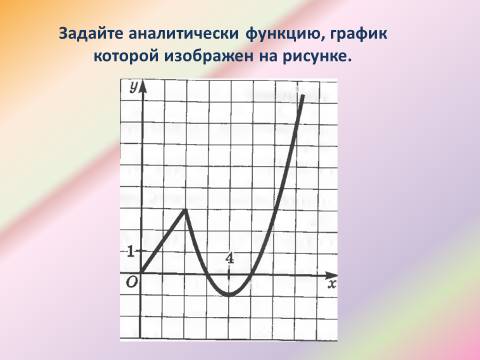
У: Задайте аналитически функцию, график которой изображен на рисунке.

8. Рефлексия деятельности на уроке

Цель этапа:

1) зафиксировать новое содержание, изученное на уроке;

2) оценить собственную деятельность на уроке;

3) поблагодарить одноклассников, которые помогли получить результат урока;

4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;

5) обсудить и записать домашнее задание.

Организация учебного процесса на этапе 8:

У: С чем мы сегодня познакомились на уроке?

Д: С кусочно-заданной функцией.

У: Какую работу мы учились сегодня выполнять?

Д: Задавать  данный вид функции аналитически .

У:  Поднимите руку, кто понял тему сегодняшнего урока?(С остальными детьми обсудить возникшие проблемы).

Домашнее задание

№21.12(а, в);  №21.13(a, в); №22.41; №22.44.

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6