
Урок по теме «Решение прямоугольных треугольников. Практическое применение»
Цель урока: Организация деятельности учащихся по обобщению понятий синус, косинус, тангенс острого угла в прямоугольном треугольнике и решению прямоугольных треугольников.
Задачи:
· образовательная: 1) Повторить понятия синус, косинус, тангенс острого угла в прямоугольном треугольнике. 2) Применить эти понятия при решении задач практического характера;
· развивающая: Создать условия контроля (самоконтроля) усвоения знаний и умений, развитие наблюдательности, внимательности, познавательного интереса;
· воспитательная: воспитание самостоятельности, аккуратности, умения отстаивать свою точку зрения, умения выслушать других.
Цели урока:
1 Повторить определения синуса, косинуса, тангенса.
2. Применять знания синуса, косинуса, тангенса при решении задач различной сложности; в практической деятельности человека;
3. Создать условия контроля (самоконтроля) усвоения знаний и умений.
4. Воспитание интереса к математике, активности, мобильности, умения вести диалог с учителем и одноклассниками.
Ход урока
2 Структура урока комплексного применения знаний и умений (урок закрепления).
1) Организационный этап.
Здравствуйте, дорогие ребята! Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Очень хочу, чтобы тот, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением, что геометрия – интересный и нужный предмет.
Давайте делиться своими идеями, которые придут вам в голову, и не бойтесь ошибиться, любая мысль может дать нам новое направление поиска. Пусть наши достижения и не покажутся кому-то крупными, но ведь это будут наши собственные достижения!
Древнегреческий философ, создатель первой высшей школы - академии Платон сказал: Не знающий геометрии да не … (не войдет в академию). А что сказал Платон? Закончите фразу.
2) Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
«Геометрия является самым могущественным средством для изощрения наших умственных способностей и даёт нам возможность правильно мыслить и рассуждать». Г.Галилей
Я прочту одну историю, а вы ответите мне: где могла произойти эта невероятная история?
Доверчивости я пою хвалу,
Но и проверка тоже не обуза…
В определенном месте, на углу
Встречались катет и гипотенуза.
У катета она была одна.
Гипотенузу он любил, не веря сплетням,
Но, в тоже время, на углу соседнем
С другим встречалась катетом она.
И дело все закончилось конфузом-
Вот после этого и верь гипотенузам.
Ответ: “эта история произошла в прямоугольном треугольнике”.
Вот и задачи сегодняшнего урока связаны с прямоугольными треугольниками.
2) Актуализация знаний. «Разминка». Фронтальный опрос.
Продолжите предложение:
1) Сторона прямоугольного треугольника, лежащего против угла в 90°, называется …(ГИПОТЕНУЗОЙ)
2) Как переводится с древнегреческого слово «гипотенуза»? (Натянутая тетива)
3) Продолжите предложение: стороны прямоугольника, образующие прямой угол называются (КАТЕТЫ)
4) Синусом острого угла прямоугольного треугольника называется (отношение противолежащего катета к гипотенузе)
5) Косинусом острого угла прямоугольного треугольника называется отношение (прилежащего катета к гипотенузе)
6) Тангенсом острого угла прямоугольного треугольника называется отношение (противолежащего катета к прилежащему катету)
7) Котангенсом острого угла прямоугольного треугольника называется отношение (прилежащего катета к противолежащему катету)
8) Значения тригонометрических функций.
3) Первичное закрепление в знакомой ситуации (типовые)
Как вы думаете, что значит решить прямоугольный треугольник?
- Под решением прямоугольных треугольников подразумевается решение задач на определение неизвестных сторон и углов прямоугольного треугольника по данным его двум элементам.
1. Витя Верхоглядкин при нахождении
синуса и косинуса острого угла прямоугольного треугольника получил следующие
числа: ![]() и
и ![]() . Не ошибся ли он?
. Не ошибся ли он?
1. Решите треугольник (индивидуально). Далее взаимопроверка в парах.
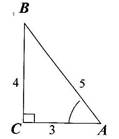
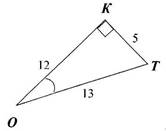
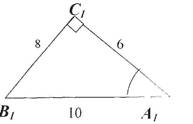
|
sin A = |
sin О = |
sin A1 = |
|
|
cos A = |
cos О = |
cos A1 = |
|
|
tg A = |
tg О =
|
tg A1 = |
|
 2.
Решить
треугольник (работа в парах)
2.
Решить
треугольник (работа в парах)
Первичное закрепление в изменённой ситуации (конструктивные)
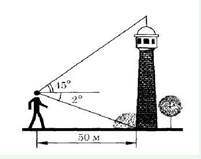 Наблюдатель
находится на расстоянии 50 м от башни, высоту которой хочет определить.
Наблюдатель
находится на расстоянии 50 м от башни, высоту которой хочет определить.
Основание башни он видит под углом 2° к горизонту, а вершину — под углом 45° к горизонту.
Какова высота башни?
Отрезок АВ=50 – расстояние от наблюдателя до башни. AB=DH=50
В прямоугольном треугольнике DСН ∠СDН=45°, значит DН=СН=50м.
В треугольнике ВНD ∠ ВDН=2°, ВН=СН·tg2°=50·0,0349≈1.75м.
Получается высота всей башни АВ=АН+ВН=50+1.75=51.75 м
Ответ: 51.75 м
5) Творческое применение и добывание знаний в новой ситуации (проблемные задания)
1. Пизанская башня известна тем, что она стоит не вертикально, а немного наклонена. Из-за этого наклона её ещё называют Падающей башней. В настоящее время наклон составляет от вертикали составляет 3° 54'. Найдите высоту башни от земли, если ее высота от основания 56 м. Решение: Н=cos 3° 54'*56= 0,9977*56=55,87м
2. Башня Сююмбике — наклонная дозорная башня Казанского кремля. Высота постройки — примерно 58 метров, а отклонение верхушки шпиля от вертикали — 1,98 метра. Найдите угол наклона башни Сююмбике.
Решение: sin A= 1,98/58=0,0341, А=2̊
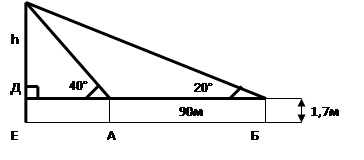
3. Задача
Какова высота скалы, если она из А видна под углом α = 40°, а из пункта Б под углом β = 20°. Расстояние между пунктами А и Б равно 90 м. Высота угломерного прибора равна 1,7м. Ответ: ͌ 60 м
6) Информация о домашнем задании, инструктаж по его выполнению.
Найти в интернете информацию о падающих башнях и придумать про них задачи.
7) Подведение итогов
Просмотр видеоролика.
Подведем итоги сегодняшнего урока. Пусть каждый из вас посчитает общее количество баллов, полученных за урок. А теперь исходя из полученных баллов поставьте себе оценку.
Уметь оперировать понятиями синус, косинус, тангенс необходимо будет и в дальнейшем, как при введении новых тем, так и в практике. Даже в 10,11 классах, при работе с объёмными фигурами эти знания часто применяются при решении задач. Поэтому очень важно усвоить весь материал и научиться его применять на практике. И как сказал Платон: «Только знающий геометрию да войдет в высшую школу!»
8) Рефлексия. Ребята предлагаю сейчас каждому из вас высказаться одним предложением, выбирая начало фразы из рефлексивного экрана на доске:
1. Мое настроение…
2. На уроке я научился…
3. Я открыл(а) для себя…
4. Я задумался(ась) над …
5. Я хотел(а) бы еще узнать …
Ребята, я уверена, что полученные на уроке знания обязательно пригодятся вам в жизни! Всего вам доброго! Благодарю за урок!
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.