"Линейная функция и ее график"

Тип урока: объяснение нового материала

Метод обучения: частично-поисковый

Цели урока. Образовательные:

-развивать умение обобщать и систематизировать изученный материал;

-выяснить зависимость положения графиков линейной функции от значений k и b;

-научить определять по значениям k и b положение графиков на координатной плоскости;

по формуле линейной функции научить определять соответствующий ей график.

  Развивающие:

-развивать способности применять теоретические знания на практике;

-развивать логическое мышление, умение применять свои знания при изучении линейной функции;

- развивать аналитические способности детей.

-развивать произвольное внимание;

-прививать культуру математической речи.

    Воспитательные:

-воспитывать интерес к изучению математики;

-воспитывать эстетику в выполнении чертежей.

=воспитывать ответственность, аккуратность

Ход урока

1.Актуализация знаний учащихся.

Вы мне, верите или нет?

1.Прямоугольная система координат на плоскости это две взаимно перпендикулярные прямые с выбранными направлениями и единицей длины? ДА

2. Точка в системе координат на плоскости имеет одну координату? НЕТ.

Как называются  координаты точки? (Ответ: абсцисса и ордината)

3. Если точка лежит на оси ординат, то ее ордината равна нулю? (НЕТ)

Если точка лежит на оси абсцисс, то ее абсцисса не  равна нулю? ( ДА)

4. Зависимость переменной у от х называют функциональной зависимостью? ( ДА)

5. Что х называют зависимой переменной? ( НЕТ) А как ее называют.

6.Вы мне верите, что функцию можно задать формулой? ( ДА). А какие еще способы задания функции вы знаете.

7. Вы мне не верите, что функция у=кх частный случай обратной пропорциональной зависимости? ( НЕТ). А какой же? ( прямой пропорциональной) Как называется к- коэффициент пропорциональности.

Дополнительно! А может вы мне приведете примеры таких зависимостей: физика(  путь и время; скорость и время;  и др.)

8. Так вы мне и не верите, что графиком функции является прямая не проходящая через начало координат. ( НЕТ) ( правильный ответ).

Тема: «Линейная функция и ее график»

Выполни устно: 1. Определить в какой четверти  расположена  точка А(x;y), если: а) x > 0, y > 0; б)  x < 0,

y > 0; в)  x < 0, y < 0; г) x > 0, y < 0.

2.Принадлежат ли графику функции y= - 0,5х  точки С (2;-1), Д (4;-20).

3. каким способом задана функция? Зависимость, каких величин представлена?

Ответьте на вопросы:

1.                                       Назовите температуру воздуха в 12 часов дня, в 18 часов вечера.

2.                                       В какое время суток температура была равна +1,8⁰С, +8,1⁰С

3.                                       В какое время суток температура была самой высокой? самой низкой?

ОПРЕДЕЛЕНИЕ: Линейной функцией называется функция, которую можно задать формулой вида y=kx+b, где x – независимая переменная, k и b – некоторые числа. Графиком линейной функции является прямая.

4.Задание 1. Работа с графиком.

1.ОПРЕДЕЛИТЬ в каких четвертях расположен график функции у=2х, построить график функции у= 2х +3. Все работают на листочках. Для построения графика нужно: 1.Составить таблицу на две точки;

2.Отметить их в системе координат; 3.Провести через эти точки прямую. Вопрос. Как расположены прямые у= 2х и у=2х+3 по отношению к друг другу? Как построить прямую у=2х-3.

Задание 2. В прямоугольной системе координат построить графики функций: у=-3х и у=-3х+3.Какой вывод можно сделать? График функции  y=kx+b,  где k0, есть прямая, параллельная прямой y=kx.( запишите в тетрадь)

Задание 3.  Построить график функции, найдя точки его пересечения с осями координат: 1)у = - 2х + 2.

Задание 4..Используя график у=х-3, заполните таблицу.                      у                    

х	-6	-3	2
у			-2   -4   X   4   -2   2   1

Задание 5.Заполни таблицу.

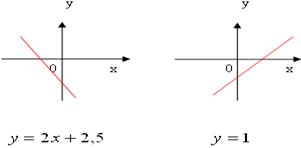
Задание 6.Ученик допустил ошибки при построении графика функции. Докажите, что графики функций построены неверно.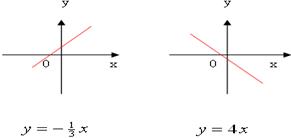 

Задание 7.а) у = 0,5х,   у = 0,5х – 2        б) у = 2х – 3,   у = - х  – 3.                              

6) Как расположены графики в системе координат?  От  чего  это  зависит?

Задание 8. Заполни пропуски в тетради.

Если b > 0, то график функции y = kx + b получается сдвигом графика функции y = kx на ______ единиц ______ (вверх/вниз) вдоль оси ______.

Если b < 0, то график функции y = kx + b получается сдвигом графика функции y = kx на ______ единиц ______ (вверх/вниз) вдоль оси ___________.

Таким образом, график функции y = kx + b получается сдвигом графика функции y = kx на ______ единиц вдоль оси ___________.

Практическая работа

Задание №1. Запишите функцию у = k х, если k=-2, в=1. Постройте ее график и определите, в каких четвертях проходит данная функция. В этой же системе постройте график у=3. Найдите точки пересечения.  Найдите по графику:  а) значения х, если у= -3, 2, 0. б) значения у, если х=0,-1,2.

№1. Разбейте функции, заданные формулами на группы: у = 2х – 3; у = 6; у = 7 х; у = 0,5х; у = - х;

у = - 12; у = 0; у = х; х=0;  у=-3х+1; у=2х; у=0,5х+2; у=3; х=2; х=-4.

Вопросы: Какие функции являются линейными? Что о них можно сказать? Как  называется число k .

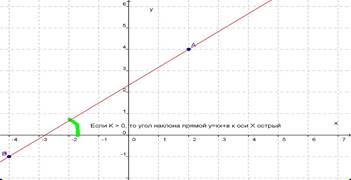
Вывод: Если k>0, то угол наклона прямой у=kx+b к оси х острый;

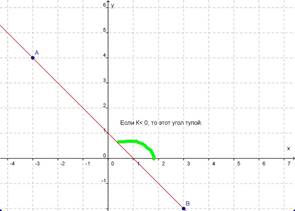
 если k<0, то этот угол тупой.

2.  Изучение нового материала. 

Линейной функцией называется функция, которую можно задать формулой вида y=kx+b, где x – независимая переменная, k и b – некоторые числа.

Графиком линейной функции является прямая.

Для построения графика линейной функции достаточно найти координаты двух точек графика, отметить эти точки на координатной плоскости и провести через них прямую.

Расположение графика функции y=kx+b на координатной плоскости зависит от коэффициентов k и b

Прямая пропорциональность является частным случаем линейной функции при b = 0.

Возьмем графики функции y = 0,5x и у = 0,5х + 2.Составим таблицы соответственных значений переменных х и у для некоторых значений аргумента х: у= 0,5х.  у= 0,5х + 2                                 

Отметим в координатной плоскости точки, координаты которых помещены в таблице.

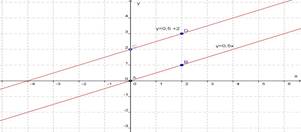
Следовательно .Если график функции у = 0,5x сдвинуть на 2 единицы вверх, то каждая точка графика функции у = 0,5х перейдет в точку графика функции у = 0,5х + 2. При этом каждая ордината точки увеличилась на 2.

График функции  y=kx+b,  где k0, есть прямая, параллельная прямой y=kx.

Если k=0, то формула  y=kx+b  принимает вид  y = b. Графиком функции        y = kx + b  является прямая, параллельная оси х при b0 или сама ось х при     b = 0. Если k=0,  b=2,  прямая проходит через точку (0;2)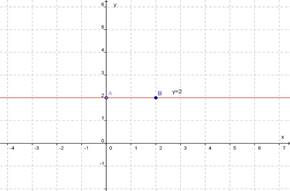

3.  Закрепление изученного материала.

Число k называется угловым коэффициентом прямой –

 графика функции у = kx + b.

Если k>0, то угол наклона прямой у=kx+b к оси х острый;

 если k<0, то этот угол тупой.

   Выводы.

Если k>0, то угол наклона, образованный графиком линейной функции, с положительным направлением оси Ох ________________________________________ .

Если k<0, то угол наклона, образованный графиком линейной функции, с положительным направлением оси Ох ________________________________________

Если k = 0, то график линейной функции расположен _____________________ оси Ох.

Если b > 0, то график функции y = kx + b получается сдвигом графика функции y = kx на ______ единиц ______ (вверх/вниз) вдоль оси ______.

Если b < 0, то график функции y = kx + b получается сдвигом графика функции y = kx на ______ единиц ______ (вверх/вниз) вдоль оси ___________.

Таким образом, график функции y = kx + b получается сдвигом графика функции y = kx на ______ единиц вдоль оси ___________.