Урок-закрепление по теме «Отношения»,6 класс

Урок-объяснение по теме «Отношения»,6 класс

Цель урока: ввести понятие отношения и процентного отношения двух чисел; определить, что показывает отношение; показать, где применяется отношение двух чисел; формировать вычислительные навыки.

Ход урока

I. Организационный момент

— Сегодня наш девиз: «Математика — это гимнастика ума».

— Как вы его понимаете?

— Что в математике позволяет тренировать наш ум?

Обратить внимание учащихся, что при нахождении отношения двух чисел очень важно понимать, какое число из двух данных чисел берется делимым, а какое - делителем.

II. Устный счет

1. Найдите 20% от чисел: 40; 200; 18; 1000; 3; 120; 0,6; 0,08..

2. Найдите значение выражений: 

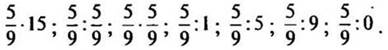
— Значение последнего выражения найти не можем, так как делить на 0 нельзя.

3. Периметр прямоугольника равен 48 см, длина на 4 см больше ширины. Найдите стороны прямоугольника.

IV. Индивидуальная работа

1 карточка

Вычислить 

2 карточка

Вычислить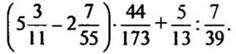 

V. Сообщение темы урока

— Сегодня на уроке мы познакомимся с понятием «отношение двух чисел» и узнаем, что оно показывает.

VI. Изучение нового материала

1. Алгоритм работы в парах (можно распечатать каждому на парту или написать на доске; можно работать под руководством учителя).

1. Прочитайте задачу 1 п. 20, стр. 117 (один ученик читает, другой слушает).

2. Разберите решение этой задачи.

3. Запишите решение в тетрадь. Если есть вопросы, обсудите их с партнером по парте или проконсультируйтесь у учителя.

4. Прочитайте 1 предложение, выделенное жирным шрифтом. Что это такое? (Определение.)

5. Запишите в тетрадь определение отношения двух чисел.

6. Выучите это определение

7. Сдайте друг другу определение, проверяя по учебнику. Если есть вопросы, выясните их с помощью учителя или партнера. Если вопросов нет, приступайте к индивидуальной работе.

2. Индивидуальная работа.

№ № учебника

8. Сверьте ответы, придите к одному решению (в паре).

9. Исправьте ошибки.

(Ответы: )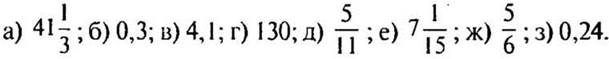

3. Фронтальная работа.

Проверка выполненных решений (проговаривание ответов). Если остается один ученик без пары, то работает с учителем, записывает решение на обратной стороне доски. Тогда возможен вариант сверки ответов с решением на доске.

Отношение — содержание, пропорция, вывод сравнения двух чисел, вычитанием (отношение арифметическое), делением (отношение геометрическое). (Из толкового словаря В. И. Даля.)

1) Давайте вернемся к рассмотренной вами задаче.

— Прочитайте ответ. Сколько вариантов ответа? (Два: один в виде обыкновенной дроби, другой — в виде десятичной, которая переведена в проценты.)

Отношение может быть выражено в процентах, тогда его называют процентным отношением.

— Что оно показывает? (Сколько процентов одно число составляет от другого.)

— Как найти процентное отношение? (Надо найти отношение и потом выразить его в процентах.)

2) Решите задачи:

(Записаны на доске или на карточках.)

1. Скорость первого пешехода равна 6 км/ч, скорость второго — 5 км/ч.

Во сколько раз скорость первого пешехода больше скорости второго пешехода?

Решение:

6 : 5 = 1,2 (раза)

(Ответ: в 1,2 раза.)

2. Первый турист прошел 12 км, второй турист — 18 км.

Какую часть пути второго туриста составляет путь первого?

Решение:

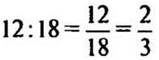 (части)

— Чтобы ответить на вопросы задач, что мы находили? (Частное.)

— Как по-другому называется частное двух чисел? (Отношением этих чисел.)

— Что показывает отношение двух чисел? (Во сколько раз первое число больше второго, или какую часть первое число составляет от второго.)

— Найдите отношения: 5 к 12; 5 к 2; 8 к 13; 13 к 8.

(Ответы: )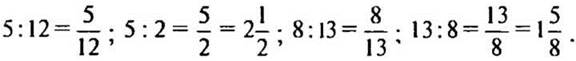

— Как по записи понять, что показывают данные отношения?

— Отношение, большее единицы, показывает, во сколько раз одно число больше (меньше) другого.

— Отношение, меньшее единицы, показывает, какую часть (дробь) одно число составляет от другого.

— Отвечая на вопросы задач, будьте очень внимательны.

— При нахождении отношения двух чисел, важно понимать, какое число из двух данных будет делимым, какое — делителем.

VII. Закрепление изученного материала

1. № № учебника (один учащийся решает на обратной стороне доски, остальные в тетрадях).

— Прочитайте задачу.

— Что надо знать, чтобы узнать, какую часть всей проволоки составляет первый кусок? (Нужно знать длину всей проволоки.)

— Как узнать длину всей проволоки? (Сложить ее части.)

— Как узнать, какую часть один кусок составляет от всей проволоки? (Найти отношение длины этого куска к длине всей проволоки.)

— Как узнать, какую часть длина первого куска составляет от длины второго куска? (Найти отношение длины первого куска к длине второго куска.)

Решение:

1) 9 + 14,4 = 23,4 (м) - длина всей проволоки.

2) 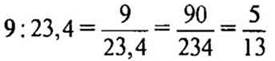 (частей) — всей проволоки составляет первый кусок.

3) 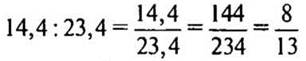 (частей) - всей проволоки составляет второй кусок.

4) 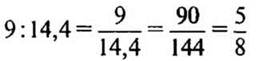 (частей) - составляет первый кусок от длины второго куска.

(Ответы: )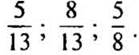

2. Устная работа

3. Самостоятельная работа.

Для мальчиков. Какую часть вашего класса составляют девочки? Ответ выразите в процентах.

Для девочек. Какую часть вашего класса составляют мальчики? Ответ выразите в процентах.

VIII. Физкультминутка

IX. Повторение изученного материала

1. № № учебника.

— Во сколько раз числитель одной дроби больше числителя другой дроби? (В 5 раз.)

— Значит, знаменатель надо увеличить тоже в 5 раз.

— Определите, на сколько нужно увеличить знаменатель дроби.

Решение:

на 8: 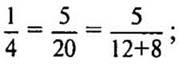 на 11: 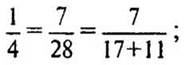 увеличивать не надо: 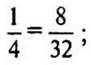 на 5: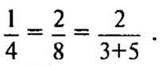 

(Ответ: 8; 11; не надо увеличивать; 5.)

2

X. Подведение итогов урока

— Что называют отношением двух чисел?

— Что показывает отношение двух чисел?

— Что такое процентное отношение двух чисел?

Выставление оценок

Домашнее задание