Урок_1_Приложение 1_Теоретический материал

Неравенство, левая часть которого многочлен второй степени, а правая часть равна нулю, называют квадратным неравенством.

Неравенства вида  и  называются строгими, а неравенства вида  и  нестрогими.

Так как неравенства  и  имеют одинаковые решения (т.е. равносильны), то можно рассмотреть решение квадратных неравенств только для случая .

Решение квадратных неравенств зависит от знака дискриминанта.

1. Пусть D < 0.

Квадратный трехчлен  можно записать так: .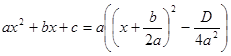

Так как   при любых х,  (т.к. D < 0) и , значение выражения  всегда положительно, т.е. неравенство  верно всегда, а неравенства  и  не выполняются ни при каких х.

2. Пусть D = 0.

Тогда равенство 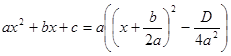 примет вид . Это выражение при  принимает неотрицательные значения. Следовательно, неравенство  верно всегда, неравенство  не выполняются ни при каких х.

3. Пусть D > 0.

Тогда квадратный трехчлен  можно записать как произведение , где  и  - корни уравнения . Положим для определенности, что .

При  оба множителя в произведении  отрицательны, поэтому выражение  принимает положительные значения.

При  множитель  положителен, а множитель  отрицателен, значит выражение  принимает отрицательные значения.

Таким образом, при  и D > 0 решение неравенства  является объединением промежутков  и , а решение неравенства  - промежуток .