
Методические рекомендации к уроку №1 темы
«Преобразования выражений, содержащих квадратные корни»
Цель обучения:
8.1.2.4
освобождать от иррациональности знаменатель дроби
На данном уроке будут рассмотрены два основных приема освобождения выражений от иррациональности знаменатель дроби.
Теоретический материал
Если знаменатель алгебраической дроби содержит знак квадратного корня, то говорят, что в знаменателе дроби содержится иррациональность. Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось квадратных корней, называют освобождением или избавлением от иррациональности в знаменателе.
Для освобождения от иррациональности в знаменателе используется два основных приема:
ü если
знаменатель имеет вид ![]() ,
то числитель и знаменатель дроби следует умножить на
,
то числитель и знаменатель дроби следует умножить на ![]() ;
;
ü если
знаменатель имеет вид ![]() или
или
![]() ,
то числитель и знаменатель дроби следует умножить на
,
то числитель и знаменатель дроби следует умножить на ![]() или
на
или
на ![]() .
.
Методические рекомендации по организации урока
В начале урока предусмотрено выполнение устных заданий (с записью ответов) с целью повторения ранее изученного материала. Способ организации деятельности учащихся на данном этапе будет способствовать развитию быстроты мышления и скорости вычислений. Задания имеют средний уровень сложности, однако учитель может упростить, или наоборот, усложнить некоторые из них в зависимости от уровня класса.
Задания нужно разрезаны на отдельные карточки. У каждого ученика должна быть одна карточка с одним заданием и таблица для записи ответов. Ученики должны быть внимательны и записать ответы на задания в ячейки с соответствующими номерами. После выполнения этой работы предусмотрено взаимооценивание: каждый ученик проверяет у остальных ответ на определенное задание. Эта работа займет немного времени, но работа учащихся над ошибками важна, поэтому можно позволить им передвигаться по классу и консультироваться с одноклассниками. Все вопросы в это время могут быть представлены на слайде.
Урок запланирован таким образом, что учащиеся будут самостоятельно изучать примеры на освобождение от иррациональности в знаменателе дроби. Материал для чтения не является сложным для восприятия. Эта работа – хорошая возможность для развития у учащихся навыка самостоятельного обучения и математической речи. К тому же ученики видят образцы грамотного оформления решения.
Для закрепления навыка освобождения от иррациональности в знаменателе дроби учащимся предлагается список задач разного уровня сложности. Более способные учащиеся возможно выполнят все задания, однако, желательно, чтобы все ученики выполнили первые 7-9 заданий.
Рекомендации по формативному оцениванию
На уроке будут использованы разные виды оценивания: взаимооценивание в начале и середине урока, оценивание учителем в конце урока при закреплении материала. На этом этапе урока можно использовать и самооценивание. Для этого поместите на доске ответы к заданиям. Разрешите учащимся подходить к доске и проверять свои ответы, затем побеседуйте о том, какие ошибки и почему были допущены первоначально, как можно было их избежать.
Ответы
Ответы к устным заданиям
|
1. При a < 3 |
2. При c ≤ 0 |
3. 3 |
4. 15 |
|
5. 14 |
6. – 9 и – 8 |
7. |
8. 4 |
|
9. |
10. |
11. |
12. |
Ответы к заданиям для письменного решения
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3)![]() ;
4)
;
4) ![]() ; 5)
; 5) ![]() ;
6)
;
6) ![]() ; 7)
; 7) ![]() ;
8)
;
8) ![]() ;
;
9) ![]() ; 10)
; 10) ![]() ; 11)
; 11) ![]() ;
12)
;
12) ![]() ; 13)
; 13) ![]() ;
14)
;
14) ![]() ; 15)
; 15) ![]() .
.
Дополнительные задания
1. Избавьтесь от иррациональности в знаменателе дроби:
а) ![]() ; б)
; б) 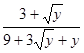 ; в)
; в) 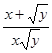 ; г)
; г)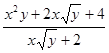 ;
;
д)![]() ; е)
; е) ![]() .
.
2. Сократить дробь: а) ![]() ; б)
; б) ![]() ; в)
; в)![]() ; г)
; г)![]() .
.
Ответы:
1. а) ![]() ; б)
; б) 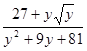 ; в)
; в) ![]() ;
г)
;
г) 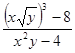 ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а)![]() ; б)
; б) ![]() ; в)
; в) ![]() ; с)
; с) ![]() .
.
Список полезных ссылок и литературы
1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 8 класс : учеб. для учащихся общеобразоват. учреждений – М. : Мнемозина, 2010. – 384 с. : ил.
2. Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Дидактические материалы. 8 класс: пособие для шк. с углубл. изучением математики – М. : Мнемозина, 2010. – 157 с. : ил.
3. Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре, 8-9 классы. – М.: Просвещение, 2009
4. Феоктистов И.Е. Алгебра. 8 класс. Дидактические материалы. Методические рекомендации. – М.: Мнемозина, 2012. – 173 с. : ил.
5.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.