Урок_2_Приложение 2_Теоретический материал

Уравнения, содержащие переменную под знаком модуля

Рассмотрим несколько уравнений, содержащих переменную (неизвестное) под знаком модуля.

Пример 1. Решить уравнение . (1)

Решение. По определению модуля если  , то а = 24 или а = -24. Следовательно, значение переменной х является корнем уравнения (1) тогда и только тогда, когда оно является корнем уравнения

 (2)

или корнем уравнения

 . (3)

Уравнение (2) имеет вид , корни которого легко определить, используя теорему Виета: x₁ = 9, x₂ = −7. Аналогично решив уравнение (3), получим: x₃ = −3, x₄ = 5.

Ответ: −7; −3; 5; 9.

Оформить решение можно следующим образом:

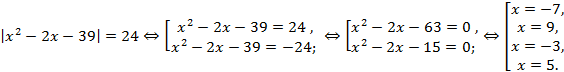
Пример 2. Решить уравнение .

Решение.  Модули двух чисел равны тогда и только тогда, когда эти числа или равны, или противоположны. Таким образом, значение x является корнем данного уравнения тогда и только тогда, когда оно является корнем уравнения

или корнем уравнения

После упрощения первое уравнение принимает вид . Сумма коэффициентов этого уравнения равна 0 (5-13+8=0), значит один из корней уравнения равен 1. По теореме Виета , отсюда .

Второе уравнение можно привести к виду . Так как для этого уравнения выполняется условие a – b + c = 0, то один из корней уравнения равен -1. По теореме Виета , поэтому .

Ответ: -1; ; 1; 1,6.

Оформление решения:

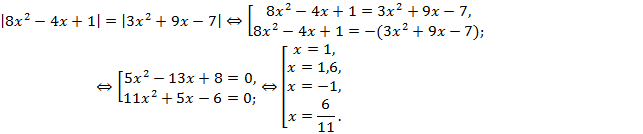
Заполните пропуски в решении уравнения .

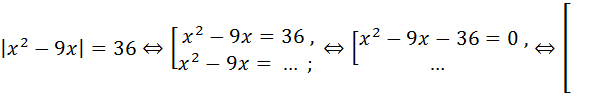
Ответ: