Урок_2_Приложения_1-4

Приложение 1

Задания для устного счета

1. При каких значениях а имеет смысл выражение  ?

2. При каких значениях с имеет смысл выражение  ?

3. Найди значение числового выражения  .

4. Найди значение числового выражения  .

5. Вычислите значение выражения  .

6. Подберите два последовательных целых числа, между которыми заключено число .

7. Упростите выражение  .

8. Укажите, сколько целых чисел принадлежит промежутку  .

9. Вынесите множитель из-под знака корня:  .

10. Вынесите множитель из-под знака корня:  , где x < 0.

11. Внесите множитель под знак корня:  .

12. Внесите множитель под знак корня:  .

Источник:

Лысенко Ф.Ф., Кулабухова С.Ю. Математика. Устные вычисления и быстрый счет. Тренировочные упражнения за курс 7 – 11 классов: учебно-методическое пособие – Ростов-на-Дону : Легион-М, 2010. – 231 с. – (Готовимся к ЕГЭ)

Лист для записи ответов

Приложение 2

Пример 1. Преобразовать заданное алгебраическое выражение к такому виду, чтобы знаменатель дроби не содержал знаков квадратных корней:

а)  ; б)  .

Решение. В обоих случаях воспользуемся основным свойством дроби: значение дроби не изменится, если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число или выражение.

а) Умножив числитель и знаменатель дроби на  , получим

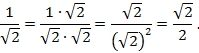
б) Умножив числитель и знаменатель дроби на  , получим

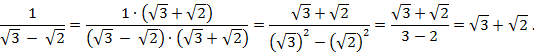
Запомни! Если знаменатель алгебраической дроби содержит знак квадратного корня, то обычно говорят, что в знаменателе дроби содержится иррациональность. Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось квадратных корней, называют освобождением или избавлением от иррациональности в знаменателе.

Два основных приема освобождения от иррациональности в знаменателе мы как раз и рассмотрели в примере 1:

ü  если знаменатель имеет вид , то числитель и знаменатель дроби следует умножить на ;

ü  если знаменатель имеет вид  или , то числитель и знаменатель дроби следует умножить на  или на .

Выражения  и  называют сопряженными.

Зачем нужно уметь освобождаться от иррациональности в знаменателе? Во многих случаях это облегчает преобразование выражений, в чем мы сейчас и убедимся.

Пример 2. Упростить выражение  .

Решение. Выполним последовательные преобразования.

1) Используйте преобразования, аналогичные пункту а) примера 1 и упростите первое слагаемое  :

2) Теперь избавимся от иррациональности в знаменателе дроби  . Используйте решение пункта б) примера 1, как образец решения и заполните пропуски:

  =

3) Таким же образом освободитель от иррациональности в знаменателе дроби :

=

4) Осталось найти алгебраическую сумму полученных результатов:

 =

Ответ: .

Использованная литература:

Звавич Л.И., Рязановский А.Р. Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений – М.: Мнемозина, 2001. – 223 с. : ил., стр. 109-110.

Приложение 3

Задания для письменного решения

Освободиться от иррациональности в знаменателе дроби:

1) ;          2) ;          3) ;          4) ;     5) ;     6) ;

7) ;            8);   9) ;    10) ;      11) ;

12) ;           13);           14) ;      15) .

Приложение 4

Освобождение дроби от иррациональности в знаменателе дроби

Письмо ученику

Освободиться от иррациональности в знаменателе дроби значит преобразовать выражение к такому виду, чтобы __________________________________________________________

__________________________________________________________

Для освобождения от иррациональности в знаменателе дроби ты можешь использовать один из следующих приемов:

1) если знаменатель дроби имеет вид __________________________

нужно _____________________________________________________

__________________________________________________________

2) если знаменатель дроби имеет вид __________________________

нужно _____________________________________________________

__________________________________________________________

Тебе следует быть внимательным при__________________________

__________________________________________________________

Желаю ___________________________________________________

___________________________________________________________________

Приложение 5

Домашнее задание

1. Освободитесь от иррациональности в знаменателе дроби:

а) ; б) ; в) ; г) ; д) ; е) .

2. Расположите в порядке возрастания числа  ;   и .

3. Докажите, что .