Урок_3_Дробно-рациональное неравенство_Методические рекомендации

Методические рекомендации к уроку №3

темы/подраздела «Рациональное неравенство»

раздела «Неравенства»

Тема урока: Решение дробно-рациональных неравенств

Цель обучения:

8.2.2.9 решать рациональные неравенства

На уроке будет рассмотрена схема решения дробно-рациональных неравенств методом интервалов.

Теоретический материал

Произведение  и частное  имеют один и тот же знак при любых значениях переменной х (за исключением нулей функций  и ), поэтому решения неравенств  и  совпадают.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

В начале урока предлагается предварительные задания, которые помогут учащимся лучше понять идеи решения дробно-рациональных неравенств. Изучение нового материала основано на обсуждении возможности применении метода интервалов к решению дробно-рациональных неравенств на основании того, что произведение и частное двух ненулевых чисел имеют одинаковые знаки.

Для первичного закрепления материала учащиеся изучат решение одного неравенства и объяснят решение партнеру. Это позволит перейти от знания к применению метода решения, не перескакивая через уровень «понимание». К тому же эта работа будет способствовать достижению языковых целей урока.

Далее учащиеся решат несколько неравенств, они могут использовать листы, выданные им во время предыдущей работы, как образец рассуждений. Решения можно обсуждать в парах, тогда более сильные учащиеся смогут оказать поддержку одноклассникам.

Ответы и решения

Решите неравенства:

Ответ:

Ответ:

Решение.

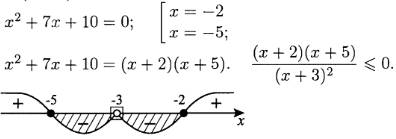
Ответ:

Решение.

Ответ:

Дополнительные разноуровневые задания

Уровень С

Решите неравенство

Решение.

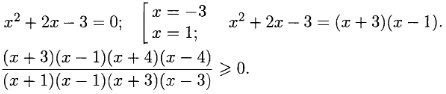
Если в нестрогом неравенстве х = а есть ко­рень в разложении числителя и знаменателя, то он обяза­тельно исключается из решения, т.е. обозначается полым кружочком. В данном случае он еще четной кратности.

Ответ:

Список полезных ссылок и литературы

1.                  Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений.  – М.: Мнемозина, 2010. – 417 с. : ил.

2.                  Шахмейстер А.Х. Дробно-рациональные неравенства.  – М.: МЦНМО, 2008. – 248 с. : ил.

3.                  https://fileskachat.com/view/30004_e60b379631adfc70dcbe7dd7010f961b.html

4.                  Скачано с www.znanio.ru