
Приложение 2
1 группа
Как избавиться от иррациональности в знаменателе дроби? Рассмотрим общий случай и конкретные примеры.
![]()
Если число или выражение, стоящее под знаком квадратного корня в знаменателе, является одним из множителей, чтобы избавиться от иррациональности в знаменателе и числитель, и знаменатель дроби умножаем на квадратный корень из этого числа или выражения:
![]()
Примеры. Освободиться от иррациональности в знаменателе дроби:
1) ![]() ;
;
2) 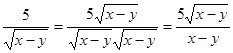 .
.
2 группа
Если знаменатель дроби — сумма либо разность двух выражений, содержащих квадратный корень, чтобы избавиться от иррациональности в знаменателе умножаем и числитель, и знаменатель на выражение, сопряженное со знаменателем:
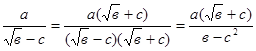 ;
;
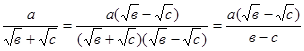
Примеры. Освободиться от иррациональности в знаменателе дроби:
1)  ;
;
2) 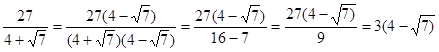 ;
;
3) 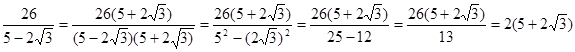
Опорные правила
Если знаменатель алгебраической дроби содержит знак квадратного корня, то говорят, что в знаменателе содержится иррациональность. Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось знаков квадратных корней, называют освобождением от иррациональности в знаменателе
Алгоритм освобождения от иррациональности в знаменателе дроби:
1. Разложить знаменатель дроби на множители.
2.
Если знаменатель имеет вид ![]() или содержит
множитель
или содержит
множитель![]() , то числитель и знаменатель
следует умножить на
, то числитель и знаменатель
следует умножить на![]() . Если знаменатель имеет
вид
. Если знаменатель имеет
вид ![]() , то числитель и знаменатель дроби
надо умножить на выражение, сопряженное знаменателю.
, то числитель и знаменатель дроби
надо умножить на выражение, сопряженное знаменателю.
3. Преобразовать числитель и знаменатель дроби, если возможно, то сократить полученную дробь.
Выражения
вида![]() и
и ![]() называются
сопряженными.
называются
сопряженными.
Задача. Преобразовать алгебраическое выражение к такому виду, чтобы знаменатель дроби не содержал знаков квадратных корней:
![]()
Решение.
Используем основное свойство дроби, то есть подбираем такой множитель, чтобы при умножении на него в знаменателе дроби не оказалось квадратных корней.
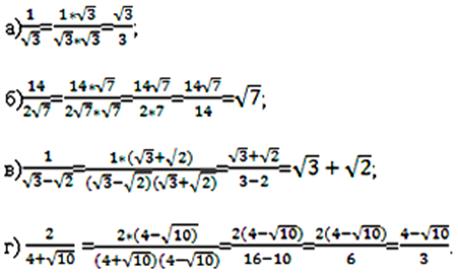
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.