Урок_4_Методические рекомендации

Методические рекомендации к уроку №4 темы/подраздела

«Преобразования выражений, содержащих квадратные корни»

раздела 8.1А: Квадратные корни и иррациональные выражения

Тема урока: Освобождение от иррациональности в знаменателе или числителе дроби

Цель обучения:

8.1.2.4

освобождать от иррациональности знаменатель дроби

Цель урока – закрепление навыка освобождения от иррациональности в знаменателе или числителе дроби.

Теоретический материал

Алгоритм освобождения от иррациональности в числителе дроби

1. Если возможно, разложить знаменатель дроби на множители.

2. Если числитель имеет вид  или содержит множитель вида , то числитель и знаменатель следует умножить на . Если числитель имеет вид  или  (или содержит множитель такого вида), то числитель и знаменатель дроби надо умножить на выражение, сопряженное знаменателю.

3. Преобразовать числитель и знаменатель дроби, если возможно, то сократить полученную дробь.

Методические рекомендации по организации урока и рекомендации по формативному оцениванию

Учащиеся уже умеют выполнять такие преобразования, как умножение выражений, содержащих квадратные корни, разложение выражений на множители, вынесение множителя из-под знака корня или внесение множителя под знак корня, избавление от иррациональности в знаменателе дроби. Поэтому на этапе актуализации знаний будут выполнены упражнения на применение этих навыков. Рекомендуется использование индивидуальных маркерных досок или ламинированных листов А4 для записи ответов. Это позволит учителю формативно оценить уровень продвижения учащихся.

Далее рассматриваются задания на избавление от иррациональности в числителе дроби. Учитель может предложить учащимся самостоятельно выработать способы действий. В зависимости от уровня продвижения класса в изучении математики учитель может вместо решения предложенных заданий (слайд 6) у доски, предложить учащимся выполнять их самостоятельно на своих маркерных досках.

Формативное оценивание уровня достижения цели урока проводится в игровой форме. Время на выполнение одного задания около 35 секунд. В зависимости от уровня своих учащихся учитель может немного изменить это время. Предложенная форма работы поможет учащимся развивать скорость мышления, увеличивать темп работы. Также положительная сторона в том, что учащиеся сразу узнают результаты своей работы и будут иметь возможность улучшить ее.

Более сложные задания рекомендуется решать совместно. Необходимость объяснить решение задания однокласснику призвано вовлечь учащихся в более детальное обсуждение решения.

Ответы и решения

Задания для формативного оценивания

Задания для работы в парах

I 1. Избавьтесь от иррациональности в знаменателе дроби

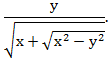
Решение.

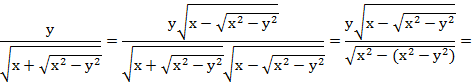
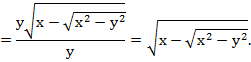
2. Упростите выражение

Решение.

II 1. Избавьтесь от иррациональности в знаменателе дроби

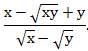
Решение.

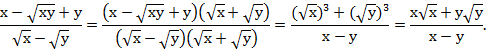
2. Упростите выражение

Решение.

Список полезных ссылок и литературы

1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 8 класс : учеб. для учащихся общеобразоват. учреждений – М. : Мнемозина, 2010. – 384 с. : ил.

2. Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре, 8-9 классы. – М.: Просвещение, 2009

3. Феоктистов И.Е. Алгебра. 8 класс. Дидактические материалы. Методические рекомендации. – М.: Мнемозина, 2012. – 173 с. : ил.

4. Зив Б.Г., Гольдич В.А. Дидактические материалы по алгебре для 8 класса. – С.-Петербург: Петроглиф, 2006

Скачано с www.znanio.ru