
Публикация является частью публикации:

Что такое софизм?
Правильно понятая ошибка – это путь к открытию
И.П. Павлов
Софизм (от греч. sophisma – уловка, выдумка, головоломка), формально кажущееся правильным, но по существу ложное умозаключение, основанное на преднамеренно неправильном подборе исходных положений.
 Каков бы ни был софизм, он обязательно содержит одну или несколько
замаскированных ошибок. Особенно часто в математических
софизмах выполняются «запрещённые» действия или не учитываются условия
применимости теорем, формул и правил. Иногда рассуждения ведутся с
использованием ошибочного чертежа или опираются на приводящие к ошибочным
заключениям «очевидности». Встречаются софизмы, содержащие
и другие ошибки.
Каков бы ни был софизм, он обязательно содержит одну или несколько
замаскированных ошибок. Особенно часто в математических
софизмах выполняются «запрещённые» действия или не учитываются условия
применимости теорем, формул и правил. Иногда рассуждения ведутся с
использованием ошибочного чертежа или опираются на приводящие к ошибочным
заключениям «очевидности». Встречаются софизмы, содержащие
и другие ошибки.

В истории развития математики софизмы играли существенную роль. Они способствовали повышению строгости математических рассуждений и содействовали более глубокому уяснению понятий и методов математики. Роль софизмов в развитии математики сходна с той ролью, какую играют непреднамеренные ошибки в математических исследованиях, допускаемые даже выдающимися математиками. Именно уяснение ошибок в математических рассуждениях часто содействовало развитию математики.

 Пожалуй, особенно поучительна в этом отношении история
аксиомы Евклида о параллельных прямых. Сформулировать эту аксиому можно так:
через данную точку, лежащую вне данной прямой, можно провести не более одной
прямой, параллельной данной (что одну прямую, параллельную данной,
можно провести – это доказывается). Это утверждение на
протяжении более чем двух тысяч лет пытались доказать, вывеси из остальных
аксиом геометрии, но все попытки не увенчались успехом. Полученные
«доказательства» оказались ошибочными. И всё же, несмотря на ошибочность этих
«доказательств», они принесли большую пользу развитию геометрии. Можно сказать,
что они подготовили одно из величайших достижений в области геометрии и всей
математики – создание неевклидовой геометрии. Честь разработки новой геометрии
принадлежит нашему великому соотечественнику Н.И. Лобачевскому и
венгерскому математику Яношу Бойяи. Н.И. Лобачевский и сам сначала пытался
доказать аксиому параллельных, но скоро понял, что этого сделать нельзя. И
путь, идя которым Лобачевский убедился в этом, привёл его к созданию новой
геометрии. Этот замечательный вклад в математику был одним из тех, которые
прославили русскую науку.
Пожалуй, особенно поучительна в этом отношении история
аксиомы Евклида о параллельных прямых. Сформулировать эту аксиому можно так:
через данную точку, лежащую вне данной прямой, можно провести не более одной
прямой, параллельной данной (что одну прямую, параллельную данной,
можно провести – это доказывается). Это утверждение на
протяжении более чем двух тысяч лет пытались доказать, вывеси из остальных
аксиом геометрии, но все попытки не увенчались успехом. Полученные
«доказательства» оказались ошибочными. И всё же, несмотря на ошибочность этих
«доказательств», они принесли большую пользу развитию геометрии. Можно сказать,
что они подготовили одно из величайших достижений в области геометрии и всей
математики – создание неевклидовой геометрии. Честь разработки новой геометрии
принадлежит нашему великому соотечественнику Н.И. Лобачевскому и
венгерскому математику Яношу Бойяи. Н.И. Лобачевский и сам сначала пытался
доказать аксиому параллельных, но скоро понял, что этого сделать нельзя. И
путь, идя которым Лобачевский убедился в этом, привёл его к созданию новой
геометрии. Этот замечательный вклад в математику был одним из тех, которые
прославили русскую науку.
Чем полезны софизмы и что они дают?
 Разбор софизмов прежде
всего развивает логическое мышление, то есть прививает навыки правильного
мышления. Обнаружить ошибку – это значит осознать её, а осознание ошибки
предупреждает от повторения её в математических рассуждениях. Что важно, разбор
софизмов помогает сознательному усвоению изучаемого материала,
наблюдательность, вдумчивость и критическое отношение к тому, что изучается. Математические
софизмы приучают внимательно и настороженно продвигаться вперёд, тщательно
точностью формулировок, правильностью записей и чертежей, за допустимостью
обобщений. Всё это нужно и важно.
Разбор софизмов прежде
всего развивает логическое мышление, то есть прививает навыки правильного
мышления. Обнаружить ошибку – это значит осознать её, а осознание ошибки
предупреждает от повторения её в математических рассуждениях. Что важно, разбор
софизмов помогает сознательному усвоению изучаемого материала,
наблюдательность, вдумчивость и критическое отношение к тому, что изучается. Математические
софизмы приучают внимательно и настороженно продвигаться вперёд, тщательно
точностью формулировок, правильностью записей и чертежей, за допустимостью
обобщений. Всё это нужно и важно.
Наконец, разбор софизмов увлекателен. Чем труднее софизм, тем большее удовлетворение доставляет его анализ.

 |
The more you forget, the less you know
The less you know, the less you forget The less you forget, the more you know So why study?
 |
 |
Вот некоторые результаты решения софизмов:
(для подробного просмотра нажмите на выбранную строку)
|
Пример 1. |
1 р. = 10 000 к. |
|
Пример 2. |
5 = 6 |
|
Пример 3. Пример 4. Пример 5. |
4 = 8 2 · 2 = 5 5 = 1 |
|
Пример 6. |
4 = 5 |
|
Пример 7. |
Любое число равно его половине |
|
Пример 8. |
Расстояние от Земли до Солнца равно толщине волоска |
|
Пример 9. |
Любое число = 0 |
|
Пример 10. |
Из двух неравных чисел первое всегда больше второго |
1 р. = 10 000 к. Возьмём верное равенство:
1 р. = 100 к. Возведём его по частям в квадрат.
 |
************************************************************************************
Вопрос:
В чём ошибка?
Ответ (нажмите «Enter»):
Возведение в квадрат величин не имеет смысла. В квадрат возводятся только числа.
Попытаемся доказать, что 5 = 6. С этой целью возьмём числовое тождество:
35 + 10 – 45 = 42 + 12 – 54.
Вынесем общие множители левой и правой частей за скобки. Получим:
5 (7 + 2 – 9) = 6 (7 + 2 – 9).
 |
(заключённый в скобки).
Получаем 5 = 6.
************************************************************************************
Вопрос:
В чём ошибка?
Ответ (нажмите «Enter»):
Общий множитель (7 + 2 – 9) равен 0, а делить на 0 нельзя.
Возьмём систему уравнений:
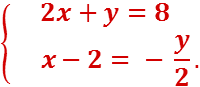
Решим её способом подстановки. Получим:
 x =
x = 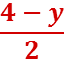 ;
;
4 – y + y = 8, т.е. 4 = 8.
************************************************************************************
Вопрос:
В чём здесь дело?
Ответ (нажмите «Enter»):
Уравнения данной системы несовместны.
Имеем числовое равенство (верное): 4 : 4 = 5 : 5. Вынесем за скобки в каждой части его общий множитель. Получим: 4 (1 : 1) = 5 (1 : 1).
 |
************************************************************************************
Вопрос:
Где здесь ошибка?
Ответ (нажмите «Enter»):
Ошибка допущена в вынесении общего множителя за скобки в левой и правой частях тождества 4 : 4 = 5 : 5.
Из чисел 5 и 1 по отдельности вычтем одно и то же число 3.
Получим числа 2 и – 2.
При возведении в квадрат этих чисел получаются равные числа
 |
************************************************************************************
Вопрос:
В чём ошибка?
Ответ (нажмите «Enter»):
Из равенства квадратов двух чисел не следует, что сами эти числа равны.
Имеем числовое равенство (верное):
 |
************************************************************************************
Вопрос:
В чём ошибка?
Ответ (нажмите «Enter»):
(4 – 4,5)2 = (5 – 4,5)2 ↔ |4 – 4,5| = |5 – 4,5|.
Возьмём два равных числа a и b, a = b. Обе части этого равенства умножим на a и затем вычтем из произведений по b2. Получим:
a2 – b2 = ab – b2, или (a + b) (a – b) = b (a – b).
 |
************************************************************************************
Вопрос:
В чём ошибка?
Ответ (нажмите «Enter»):
Нельзя делить на (a – b), так как (a – b) = 0.
Пусть a (м) – расстояние от Земли до Солнца, а b (м) – толщина волоска. Среднее арифметическое их обозначим через v. Имеем:
a + b = 2v, a = 2v – b, a – 2v = – b. Перемножив по частям два последних равенства, получаем:
 |
************************************************************************************
Вопрос:
Где здесь ошибка?
Ответ (нажмите «Enter»):
Ошибка как в примере №6.
Каково бы ни было число a, верны равенства:
 |
************************************************************************************
Вопрос:
В чём ошибка?
Ответ (нажмите «Enter»):
Ошибка как в примере №6.
Из двух неравных чисел первое всегда больше второго
Пусть a и b – произвольные числа и a ≠ b. Имеем:
(a – b)2 > 0, т.е. a2 – 2ab – b2 > 0, или a2 + b2 > 2ab. К обеим частям этого неравенства прибавим – 2b2. Получим:
 |
************************************************************************************
Вопрос:
Где допущена ошибка?
Ответ (нажмите «Enter»):
При делении обеих частей неравенства (a + b) (a – b) > 2b (a – b) на (a – b) знак неравенства может измениться на противоположный (если a – b < 0).
Вот некоторые примеры геометрических софизмов:
(для подробного просмотра нажмите на выбранную строку)
 |
 Пример 1. Загадочное
исчезновение.
Пример 1. Загадочное
исчезновение.
Пример 2. Земля и апельсин
Пример 3. Искусная починка
Пример 4. Два перпендикуляра
Пример 5. «Новое доказательство» теоремы Пифагора
У нас есть произвольный прямоугольник, на котором начерчено 13 одинаковых линий на равном расстоянии друг от друга, так, как
 |
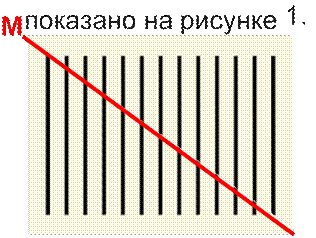 Теперь «разрежем» прямоугольник прямой MN, проходящей через верхний конец
первой и нижний конец последней линии. Сдвигаем обе половины вдоль по этой линии и замечаем, что линий
вместо 13 N стало 12. Одна
линия исчезла бесследно.
Теперь «разрежем» прямоугольник прямой MN, проходящей через верхний конец
первой и нижний конец последней линии. Сдвигаем обе половины вдоль по этой линии и замечаем, что линий
вместо 13 N стало 12. Одна
линия исчезла бесследно.
Рис. 1
************************************************************************************
Вопрос:
Куда исчезла 13-я линия?
Ответ (нажмите «Enter»):
13-я линия удлинила каждую из оставшихся на 1/12 своей длины .
Вообразим, что земной шар обтянут по экватору обручем и что подобным же образом обтянут и апельсин по его большому кругу. Далее вообразим, что окружность каждого обруча удлинилась на 1м. Тогда обручи отстанут от поверхности тел и образуют некоторый зазор
************************************************************************************
Вопрос:
Где зазор будет больше: у апельсина или у Земли?
 Ответ (нажмите «Enter»):
Ответ (нажмите «Enter»):
Пусть длина окружности земного шара = C, а апельсина с метрам. Тогда радиус Земли R = C/2 и радиус апельсина r = c/2 . После прибавки к радиусам 1 метра окружность обруча у Земли будет C + 1, а у апельсина c + 1. Радиусы их соответственно будут: (C + 1)/2 и (c + 1)/2 . Если из новых радиусов вычтем прежние, то получим в обоих случаях одно и то же.
(C + 1)/2 - C/2 = 1/2 - для Земли,
(c + 1)/2 - c/2 = 1/2 - для апельсина Итак, у Земли и у апельсина получается один и тот же зазор в 1/2 метра (примерно 16 см).
Искусная починка
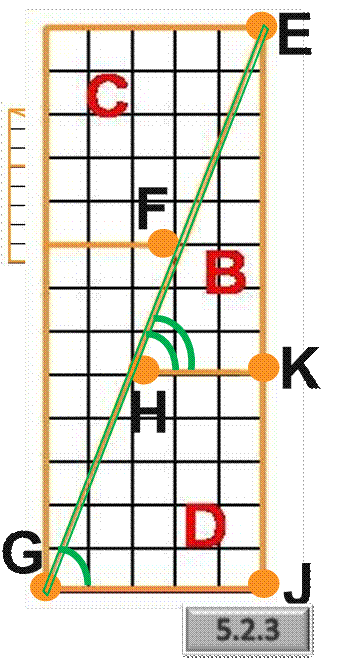
В дне деревянного судна во время плавания случилась прямоугольная пробоина в 13 см длины и 5 см ширины, т.е. площадь пробоины = 65 см2. Судовой плотник взял квадратную дощечку со стороной квадрата 8 см (т.е. площадь = 64 см2), разрезал её прямыми линиями на четыре части A, B, C, D так, как показано на рисунке 2, а затем сложил их так, что получился прямоугольник, как раз соответствующий пробоине, см. рисунок 3. Этим прямоугольником он и заделал пробоину. Вышло, что плотник сумел квадрат в 64 см2 обратить в прямоугольник с площадью 65 см2.
*******************************************************
 Вопрос:
Вопрос:
Как такое могло получиться? Ответ (нажмите «Enter»):
Легко видеть, что получившиеся при разрезании квадрата треугольники A и B равны между собой. Также равны и трапеции C, D. Меньшее основание трапеций и меньший катет треугольников равны 3 см и поэтому должны совпасть при совмещении треугольника A с трапецией C и треугольника B с трапецией D. В чём же секрет? Дело в том, что точки G, H, E не лежат на одной прямой, tg EHK = 8/3 , а tg HGJ = 5/2. Так как 8/3 – 5/2 = 1/6 > 0, то EHK > HGJ. Точно так же линия EFG – ломанная. Площадь полученного прямоугольника действительно равна 65 см2, но в нём имеется щель в виде параллелограмма, площадь которого в точности равна 1 см2. Наибольшая ширина щели равна 5 – 3 – (5·3)/8 = 1/8 см. Таким образом плотнику всё равно придётся замазывать небольшую щель.
 Попытаемсяпрямой, к этой «доказать», прямой можно что
провестичерез точку, два перпендикуляра лежащую вне. . 4 B
Попытаемсяпрямой, к этой «доказать», прямой можно что
провестичерез точку, два перпендикуляра лежащую вне. . 4 B
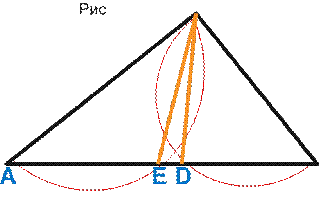
С этой целью возьмём треугольник ABC (рисунок 4). На сторонах AB и BC этого треугольника, как на диаметрах, построим полуокружности. Пусть эти полуокружности пересекаются со стороной AC в точках E и D. Соединим точки E и D прямыми с точкой B. Угол AEB прямой, как вписанный, опирающийся на диаметр; угол BDC также прямой.
Следовательно, BE AC и BD AC. Через точку B проходят C два перпендикуляра к прямой AC.
 ****************************************************
****************************************************
Вопрос: B
В чём ошибка?
Ответ (нажмите «Enter»):
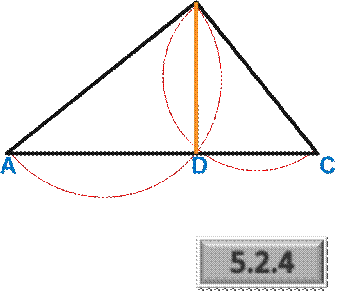
Рассуждения опирались на ошибочный чертёж. В действительности полуокружности пересекаются со стороной AC в одной точке, т.е. BE совпадает с BD.
Возьмём прямоугольный треугольник с катетами a и b, гипотенузой c и острым углом , противолежащим катету a.
Имеем: a = c sin , b = c cos , откуда a2 = c2 sin2 , b2 = c2 cos2 . Просуммировав по частям эти равенства, получаем:
 |
************************************************************************************
Вопрос:
В чём ошибка?
Ответ (нажмите «Enter»):
Ошибки здесь нет. Но формула sin2 + cos2 = 1 сама выводится на основании теоремы Пифагора.
1. «Аванта +. Математика». – Москва, изд. «Аванта +»,1998.
2. «БЭКМ – 2007». – Москва, 2007.
3.

 |
4. Нагибин Ф.Ф., Канин Е.С. «Математическая шкатулка». – Москва, изд. «Просвещение»,1988.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.