Вопрос 42.doc

          Решение задачи Коши для обыкновенных дифференциальных уравнений.

Требуется найти решение уравнения y’=f(x,y) (1) при начальном условии y(x₀)=y₀ (2). Пара чисел (x₀,y₀) называется начальными данными. Решение задачи Коши называется частным решением уравнения (1) при условии (2). Частному решению соответствует одна из интегральных кривых, проходящих через точку (x₀,y₀). Условие существования и единственности решения задачи Коши содержится в теореме: Пусть функция f(x,y) – правая часть ДУ (1), непрерывна вместе со своей частной производной 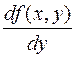 по переменной y в некоторой области D на плоскости. Тогда при любых начальных данных (x₀,y₀) задача Коши (1)-(2) имеет единственное решение . При выполнении условий теоремы через точку (x₀,y₀) на плоскости проходит единственная интегральная кривая.

Численное решение задачи Коши состоит в том, чтобы получить искомое решение в виде таблицы значений аргументов на некотором отрезке [a,b]. x₀=a,x₁,…,x_n=b. Точки x_i, i= называются узловыми точками, а множество этих точек называется сеткой на отрезке [a,b]. Будем использовать равномерную сетку с шагом h=(b–a)/n, x_i–x_i–1=h, x_i=x₀+ih, i=. Приближенное значение численного решения задачи Коши в узловых точках  x_i обозначим Y_i. Т.о. , i=. Для любого численного метода решения задачи Коши условие (2) выполняется точно, т.е. . Величина погрешности численного метода решения задачи Коши на сетке отрезка  [a,b] оценивается величиной , т.е. расстояние между векторами приближенного решения (Y₀, Y₁,…, Y_n) и точного решения  на сетке, в метрике и на . Говорят, что численный метод имеет p-тый порядок точности по шагу h на сетке, если расстояние d можно представить в виде степенной функции от h.d=ch^p, p>0, c – положительный постоянный коэффициент. В данном случае, когда шаг , то погрешность .

Метод Эйлера и его модификации, методы Рунге-Кутта.

Задача Коши для ДУ вида y’=f(x,y) состоит в том, чтобы найти решение этого уравнения, удовлетворяющее условию y(x₀)=y₀. Простейшим численным методом решения задачи Коши является метод Эйлера (метод ломаных Эйлера). Угловой коэффициент касательной к интегральной кривой в точке P₀(x₀,y₀) есть . Найдем ординату y₁ касательной, соответствующей абсциссе . Уравнение касательной к кривой в точке P₀ имеет вид: , тогда . Угловой коэффициент в точке P₁(x₁,y₁) также находится из данного ДУ: . На следующем шаге получаем новую точку P₂(x₂,y₂), причем . Продолжая вычисления в соответствии с изложенной схемой, получаем формулы Эйлера для n приближенных значений решения задачи Коши с начальными данными (x₀,y₀) на сетке отрезка [a,b] с шагом h_..  (1). Графической иллюстрацией приближенного решения является ломаная, соединяющая последовательно точки P₀, P₁,…, P_n, которая называется ломаной Эйлера.

Оценим погрешность метода на одном шаге. Для этого запишем разложение точного решения задачи Коши в точке x₁ по формуле Тейлора с остаточным членом в форме Лагранжа:

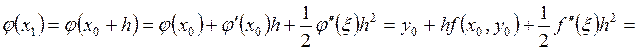
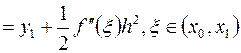. Погрешность метода на одном шаге имеет порядок h², т. к.

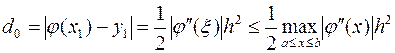. После n шагов погрешность вычисления значения в конечной точке отрезка возрастет не больше чем в n раз. Погрешность метода Эйлера можно оценить неравенством: 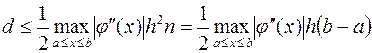 или d=ch, где 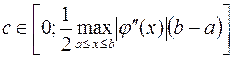. Это означает, что метод Эйлера имеет первый порядок точности. В частности, при уменьшении шага h в 10 раз, погрешность тоже уменьшится примерно в 10 раз. Практическую оценку погрешности решения на сетке отрезка [a,b] с шагом h/2 в точке x_i[a,b] производят с помощью приближенного равенства – правила Рунге: 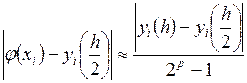,    где p – порядок точности  численного метода. Т. о. оценка погрешности полученного результата проводится с помощью 2-х вычислений: один раз с шагом h, второй раз – с шагом h/2.

Численный метод решения задачи Коши на равномерной сетке x₀=a, x₁,…, x_m=b  отрезка [a,b] шагом 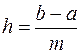, является методом Рунге-Кутта, если, начиная с данных (x₀,y₀) решение ведется по следующим рекуррентным формулам:   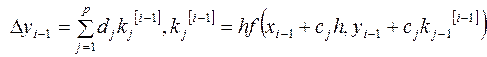(2). Метод называется методом Рунге-Кутта порядка p, если он имеет p-тый порядок точности по шагу h на сетке. Порядок точности p достигается с помощью формулы (1) при определенных значениях коэффициентов c_j и d_j , j=, c₁=0 всегда. Эти коэффициенты вычисляются по следующей схеме: 1) точное решение  и его приближение  представляются в виде разложения по формуле Тейлора с центром x₀, вплоть до слагаемого порядка ; 2) из равенств подобных членов при одинаковых степенях h в двух разложениях получают уравнения, решая которые находят коэффициенты .

Метод Эйлера можно назвать методом Рунге-Кутта 1-го порядка. Действительно, для p=1, c₁=0, d₁=1 формулы (2) преобразуются в соотношения (1).

Метод Рунге-Кутта 2-го порядка (p=2) называется методом Эйлера-Коши.  Если p=2, то c₁=0, c₂=1, d₁=d₂=1/2. В этом случае формулы (2) принимают вид: ,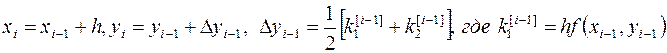

  (7). Для практической оценки погрешности приближения можно применить правило Рунге, полагая p=2.

Метод Рунге-Кутта 4-го порядка называют классическим методом Рунге-Кутта. p=4, c₁=0, c₂=c₃=1/2, c₄=1, d₁=d₄=1/6, d₂=d₃=1/3, получим классические формулы Рунге-Кутта:

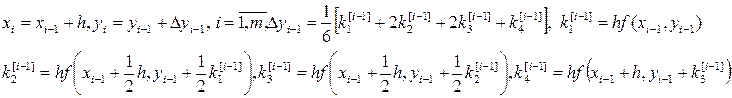
Графиком приближенного решения является ломаная, последовательно соединяющая точки P_i(x_i,y_i), i=. С увеличением порядка численного метода звенья  ломаной приближаются к ломаной, образованной хордами интегральной кривой , последовательно соединяющими точки на интегральной кривой. Правило Рунге практической оценки погрешности решения для численного метода 4-го порядка имеет вид: