
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УО «МОЗЫРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ
УНИВЕРСИТЕТ ИМ. И. П. ШАМЯКИНА»
Кафедра физики и математики
МЕТОДИЧЕСКИЙ ПРОЕКТ
«ВПИСАННЫЕ И ОПИСАННЫЕ МНОГОУГОЛЬНИКИ»
Выполнила студентка 4 курса 1группы
физико-инженерного факультета
дневной формы обучения
Домасевич Кристина Сергеевна
Мозырь 2018
СОДЕРЖАНИЕ
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
§ 1. Взаимное расположение прямой и окружности. Касательная к окружности
1.Взаимное расположение прямой и окружности.
2. Касательная к окружности.
3. Взаимное расположение двух окружностей.
§ 2. Центральные и вписанные углы
1. Центральные углы. Градусная мера дуги окружности.
2. Вписанные углы.
3. Свойство пересекающихся хорд. Теорема о касательной и секущей.
§ 3. Замечательные точки треугольника
1.Теорема о точке пересечения биссектрис треугольника.
2.Теорема о точке пересечения прямых, содержащих высоты треугольника..…
§ 4. Вписанные и описанные треугольники
1. Окружность, вписанная в треугольник.
2. Окружность, описанная около треугольника
§ 5. Вписанные и описанные четырехугольники
1. Окружность, вписанная в четырехугольник.
2. Окружность, описанная около четырехугольника
ТИПОВЫЕ ЗАДАЧИ
КОНТРОЛЬНЫЕ РАБОТЫ
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
ПРИЛОЖЕНИЕ 1
ПРИЛОЖЕНИЕ 2
ПРИЛОЖЕНИЕ 3
ПРИЛОЖЕНИЕ 4
ПРИЛОЖЕНИЕ 5
ЗАКЛЮЧЕНИЕ
СПИСОК ЛИТЕРАТУРЫ
Тема «Вписанные и описанные многоугольники» изучается в 9 классе.
В данной теме рассматриваются следующие вопросы:
1. Взаимное расположение прямой и окружности.
2. Касательная к окружности. Центральные и вписанные углы.
3. Измерение центральных и вписанных углов.
4 .Взаимное расположение окружностей.
5. Замечательные точки треугольника.
6. Окружность, описанная около треугольника.
7. Окружность, вписанная в треугольник.
8. Вписанные и описанные четырехугольники.
Основная цель: познакомить учащихся с простейшими телами вращения и их свойствами.
Рассмотрением простейших тел вращения завершается формирование системы основных пространственных геометрических фигур, изучаемых в школьном курсе стереометрии: в рассмотрение вводятся цилиндр, конус, шар и сфера. Одновременно с определением конкретного тела вращения даются определения большому числу понятий, связанных с ним (высота, радиус, ось цилиндра и т. д.); усвоение которых должно идти не по линии формального воспроизведения их определений, а в ходе решения содержательных геометрических задач. При изучении теоретического материала развиваются пространственные представления учащихся: с общим понятием "тела вращения" они знакомятся на примерах рассматриваемых геометрических фигур; изучают вопросы взаимного расположения тел вращения и плоскости: сечения цилиндра, конуса, шара; касательную плоскость; знакомятся с понятиями вписанных и описанных призм и пирамид. Логические и графические умения учащихся развиваются в ходе решения задач, требующих распознавания различных тел вращения и их сечений, построения соответствующих чертежей. Понятие объема и его свойства могут быть изучены на ознакомительном уровне с опорой на наглядные представления и жизненный опыт учащихся. При выводе формул объема конуса широко привлекаются приближенные вычисления и интуитивные представления учащихся о предельном переходе. От учащихся можно не требовать воспроизведения вывода этих формул. Вывод формулы объема шара проводится с использованием интеграла. Его можно выполнить в качестве решения задачи на уроках алгебры и начал анализа. Материал, связанный с выводами общей формулы объемов тел вращения, имеет служебный характер: с ее помощью затем выводится формула объема шара.
1) прямая имеет только две общие точки с окружностью;
2) прямая имеет только одну общую точку с окружностью;
3) прямая не имеет общих точек с окружностью.
Если прямая имеет две общие точки с окружностью, то она называется секущей. Взаимное расположение окружности ω(O, R) с центром в точке O радиуса R и прямой характеризуется соотношением между расстоянием d(O, l) от центра O окружности до прямой l и радиусом R окружности. Докажем это.
Прямая l имеет только две общие точки с окружностью, если расстояние от центра окружности до прямой l меньше радиуса окружности, т. е. если d(O, l) < R (рис. 1).
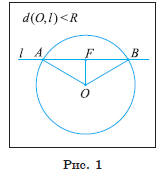
1) Пусть прямая l не
проходит через центр O окружности и рaсстояние d(O, l) = m, m
R. Обозначим OF (F ∈ l) — перпендикуляр, проведенный из точки O к прямой l,
тогда OF =m. Пусть точки A
и B лежат на прямой l так, что FA = FB =![]() . Докажем, что
точки A и B принадлежат окружности.
. Докажем, что
точки A и B принадлежат окружности.
Действительно, так как по теореме Пифагора
![]() и
и ![]() . Таким образом, точки A и B — общие
точки прямой и окружности. Докажем,
. Таким образом, точки A и B — общие
точки прямой и окружности. Докажем,
что других общих точек прямая l и окружность ω(O, R) не имеют.
Предположим, что существует еще одна точка
X — общая для окружности и прямой. Тогда центр окружности O равноудален от точек A, B, и X, а значит,
он лежит на серединных перпендикулярах ![]() и
и ![]() к отрезкам AB
и BX, т. е. O — точка перессечения серединных перпендикуляров
к отрезкам AB
и BX, т. е. O — точка перессечения серединных перпендикуляров ![]() и
и ![]() , то
, то ![]() . Получили противоречие. Значит, наше предположение не
верно и других общих точек прямой и окружности нет. Если прямая l проходит
через центр O окружности, т. е.
d(O, l) = 0, то она пересекает окружность в двух точках, которые
являются концами диаметра, лежащего на этой
прямой.
. Получили противоречие. Значит, наше предположение не
верно и других общих точек прямой и окружности нет. Если прямая l проходит
через центр O окружности, т. е.
d(O, l) = 0, то она пересекает окружность в двух точках, которые
являются концами диаметра, лежащего на этой
прямой.
2) Прямая l имеет только одну общую точку с окружностью, если расстояние от центра окружности до прямой l равно радиусу окружности, т. е. если d(O, l) = R. Пусть расстояние от центра окружности до прямой l равно радиусу окружности, а точка F — основание перпендикуляра, проведенного из центра окружности к прямой l (рис. 2).
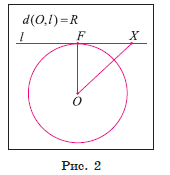
Тогда OF = R, а значит, точка F лежит на окружности. Других общих точек прямая и окружность не имеют. Действительно, для любой точки X прямой l, не совпадающей с точкой F, выполняется условие OX > OF, OF = R, так как наклонная OX больше перпендикуляра OF. Следовательно, точка X не лежит на окружности.
3) Прямая l не имеет общих точек с окружностью, если расстояние от центра O окружности до прямой l больше радиуса окружности, т. е. если
d(O, l) > R. Пусть расстояние от центра O окружности до прямой l больше радиуса R. Обозначим буквой F основание перпендикуляра, проведенного из центра O окружности к прямой l (рис. 3). Тогда OF = d(O, l), d(O, l) > R.
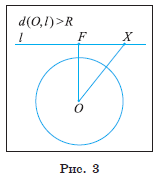
Для любой точки X прямой выполняется условие OX ≥ OF > R, следовательно, точка X не лежит на окружности. Таким образом, в случае d(O, l) R прямая и окружность не имеют общих точек.
Определение. Касательной к окружности называется прямая, которая имеет с окружностью только одну общую точку.
Единственная общая точка прямой и окружности называется точкой касания прямой и окружности.
Если прямая l имеет единственную общую точку A с окружностью, то говорят, что прямая l касается окружности в точке A.
Теорема 1 (о свойстве касательной). Касательная к окружности перпендикулярна радиусу этой окружности, проведенному в точку касания.
Доказательство.
1) Пусть прямая l касается окружности ω(O, R) в точке A (рис. 4). Докажем, что l ⊥ OA.
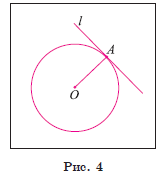
2) Предположим, что это не так. Тогда радиус OA является наклонной к прямой l. Перпендикуляр, проведенный из точки O к прямой l, меньше наклонной OA, следовательно, расстояние от центра окружности до прямой меньше радиуса. Значит, прямая и окружность имеют две общие точки, что противоречит условию. Таким образом, прямая l перпендикулярна радиусу OA.
Теорема доказана.
Рассмотрим следствия из данной теоремы.
Пусть через точку A проведены две прямые, касающиеся окружности ω(O, R) в точках C и B. Тогда отрезки AB и AC называются отрезками касательных, проведенными из точки A (рис. 5).
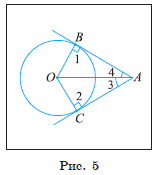
Следствие 1. Отрезки касательных к окружности, проведенные из одной точки, равны.
Доказательство.
1) Пусть AB и AC — отрезки касательных, проведенные из точки A (рис. 5). Для доказательства равенства AB = AC рассмотрим треугольники ABO и ACO.
2) По свойству касательной ∠ 1 = 90° и ∠ 2 = 90°, т. е. треугольники ABO и ACO — прямоугольные.
3) ∆ ABO = ∆ ACO, так как AO — общая гипотенуза, а катеты OB и OC равны как радиусы окружности. Отсюда следует, что AB = AC. Следствие 1 доказано. Из равенства треугольников ABO и ACO вытекает также, что ∠ 3 = ∠ 4. Таким образом, получим еще одно следствие.
Следствие 2. Отрезки касательных к окружности, проведенные из одной точки, составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Теперь докажем признак, который позволяет устанавливать, в каком случае прямая касается окружности. Оказывается, для этого достаточно установить, что прямая перпендикулярна радиусу и проходит через его конец, лежащий на окружности.
Теорема 2 (признак касательной). Если прямая перпендикулярна радиусу окружности и проходит через его конец, лежащий на окружности, то она касается этой окружности.
Доказательство.
1) Пусть прямая l проходит через точку A окружности и перпендикулярна радиусу OA (рис. 6). Для доказательства того, что прямая l касается окружности, достаточно доказать, что она имеет с этой окружностью единственную общую точку.
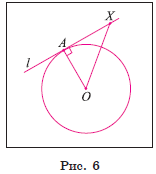
2) Так как точка A лежит на окружности и прямая l проходит через точку A, то A — общая точка прямой l и окружности.
3) Других общих точек прямая l и окружность не имеют. Действительно, для любой точки X ∈ l отрезок OX является наклонной, так как по условию OA ⊥ l. Следовательно, OX > OA, т. е. точка X не принадлежит окружности.
Таким образом, точка A — единственная общая точка прямой l и окружности, а, значит, прямая l — касательная к окружности.
Теорема доказана.
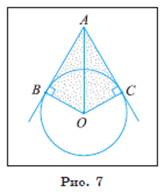
Задача 1. Через точку A, находящуюся от центра O окружности на расстоянии 10 см, проведены две касательные AB и AC, где B и С — точки касания. Вычислите площадь SABOC четырехугольника ABOC, если AB + AC == 16 см ( рис. 7).
Решение.
1) Площадь четырехугольника ABOC равна сумме площадей треугольников ABO и ACO.
2) По свойству касательной ∠ OBA = ∠ OCA = 90°. Прямоугольные треугольники ABO и ACO равны по
гипотенузе и катету (AO — общая, OB = OC). Значит,![]()
3) Отрезки касательных к окружности, проведенные из одной точки, равны. Следовательно, AB = AC = 8 см. Теперь, применив теорему Пифагора, вычислим
![]()
Таким образом, ![]()
Ответ: ![]() .
.
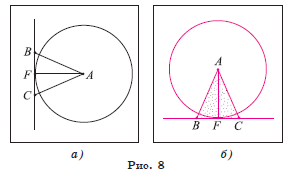
Задача 2. Точка F — середина основания BC равнобедренного треугольника ABC. Докажите, что прямая BC является касательной к окружности ω(A, AF) (рис. 8, а, б).
Доказательство.
1) Прямая BC проходит через конец F радиуса окружности ω(A, AF). Для доказательства того, что BC является касательной, достаточно доказать, что BC ⊥ AF.
2) В равнобедренном треугольнике ABC отрезок AF — медиана, проведенная к его основанию. Следовательно, AF ⊥ BC. Таким образом, по признаку касательной прямая BC касается окружности ω(A, AF).
Что и требовалось доказать.
Задача 3. Точка A лежит вне окружности ω(O, R). Постройте прямую, которая касается окружности и проходит через точку A.
Поиск решения.
1) Пусть прямая l, проходящая через точку A и касающаяся окружности ω(O, R), построена. Точка B — точка касания. Тогда по свойству касательной OB ⊥ AB (рис. 9, а). Следовательно, для построения искомой касательной необходимо построить точку B на окружности ω(O, R) так, что OB ⊥ AB.
2) Рассмотрим окружность ω1,
диаметром которой является отрезок AO, т. е. ![]() Пусть B и C — точки
пересечения окружностей ω(O, R) и
Пусть B и C — точки
пересечения окружностей ω(O, R) и ![]() (рис. 9, б). Заметим, что ∠
1 =
∠ 2 и ∠ 3 = ∠ 4, как углы при основании равнобедренных треугольников
(рис. 9, б). Заметим, что ∠
1 =
∠ 2 и ∠ 3 = ∠ 4, как углы при основании равнобедренных треугольников
![]() и
и ![]() соответственно. Так как ∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 = 180°, то ∠ 1 + ∠ 3 = ∠ 2 + ∠ 4 = 90°. Значит, ∠ OBA = 90°, т. е. OB ⊥
AB. Аналогично доказывается,
что OC ⊥ AC. Отсюда по признаку касательной к окружности
следует, что прямые AB и AC являются касательными. Теперь понятна
последовательность необходимых построений.
соответственно. Так как ∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 = 180°, то ∠ 1 + ∠ 3 = ∠ 2 + ∠ 4 = 90°. Значит, ∠ OBA = 90°, т. е. OB ⊥
AB. Аналогично доказывается,
что OC ⊥ AC. Отсюда по признаку касательной к окружности
следует, что прямые AB и AC являются касательными. Теперь понятна
последовательность необходимых построений.
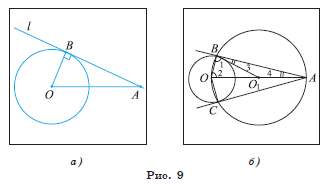
Построение.
1) Проводим отрезок OA, соединяющий центр О данной окружности и точку A (рис10,а).
2) Строим середину O1 отрезка OA: O FE OA 1 = ∩ .
Точки F и E — точки пересечения окружностей ω2(O, r) и ω3(A, r), где ![]() (рис. 10, б).
(рис. 10, б).
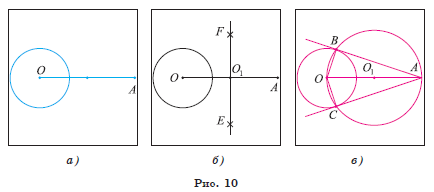
3) Строим окружность ω1(O1, O1A) (рис. 10, в) и точки B, C — точки пересечения данной и построенной окружностей.
4) Прямые AB и AC — искомые касательные к данной окружности.
Доказательство.
По построению ∠OBA = 90° и ∠OCA = 90° (см. задачу № 251 учебного пособия «Геометрия, 7»), т. е. AB ⊥ OB и AC ⊥ OB. Следовательно, по признаку касательной AB и AC — касательные.
1) окружности не имеют общих точек (в этом случае говорят, что они не пересекаются (рис. 11, а ));
2) окружности имеют две общие точки (в этом случае говорят, что окружности пересекаются (рис. 11, б));
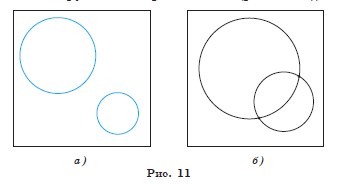
3) окружности имеют только одну общую точку, и одна из окружностей лежит внутри круга, ограниченного другой окружностью (в этом случае говорят, что они касаются внутренним образом (рис. 12, а ));
4) окружности имеют только одну общую точку, и ни одна из окружностей не лежит внутри круга, ограниченного другой окружностью (в этом случае говорят, что они касаются внешним образом (рис. 12, б)).
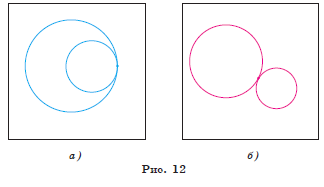
Задача 1. Докажите, что если две окружности ![]() касаются внешним образом, то расстояние между их
центрами равно сумме их радиусов, т. е.
касаются внешним образом, то расстояние между их
центрами равно сумме их радиусов, т. е. ![]() .
.
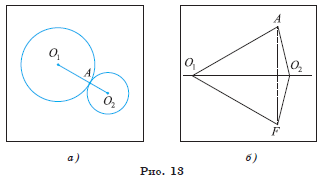
Доказательство.
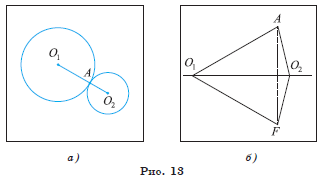
1) Пусть окружности![]() касаются
внешним образом в точке A (рис. 13, а).
касаются
внешним образом в точке A (рис. 13, а).
2) Докажем, что точка A лежит на
отрезке ![]() . Допустим, что точка A не лежит
на отрезке
. Допустим, что точка A не лежит
на отрезке ![]() . Заметим, что в случае внешнего касания точка A не может
лежать на продолжении отрезка
. Заметим, что в случае внешнего касания точка A не может
лежать на продолжении отрезка ![]() . Пусть точка касания A не лежит
на отрезке
. Пусть точка касания A не лежит
на отрезке ![]() (рис. 13, б). Тогда
(рис. 13, б). Тогда ![]() A =
A =
![]() и
и ![]() A =
A =
![]()
3) Пусть F — точка, симметричная точке
A относительно прямой ![]() . Окружности
. Окружности![]() имеют две общие точки, что противоречит условию их
касания. Следовательно, точка касания A
лежит на отрезке
имеют две общие точки, что противоречит условию их
касания. Следовательно, точка касания A
лежит на отрезке ![]() .
.
4) Докажем, что ![]() . Точка A лежит на отрезке
. Точка A лежит на отрезке ![]() , значит,
, значит, ![]() .
.
Теорема доказана.
Справедливо и обратное утверждение.
Задача 2. Докажите, если расстояние между центрами двух окружностей, лежащих в плоскости, равно сумме их радиусов, то такие окружности касаются внешним образом.
Доказательство.
1) Пусть даны две окружности ![]() и известно, что
и известно, что ![]() . Докажем, что окружности касаются внешним образом.
. Докажем, что окружности касаются внешним образом.
2) На отрезке ![]() рассмотрим точку A такую, что
рассмотрим точку A такую, что ![]() A =
A = ![]() . Тогда
. Тогда ![]() A =
A =
![]() −
− ![]() A = (
A = (![]() +
+ ![]() ) −
) − ![]() =
= ![]() . Таким
. Таким
образом, точка A принадлежит каждой из данных окружностей.
3) Докажем,
что окружности не имеют других общих точек. Действительно, на прямой ![]() таких точек нет. Предположим, что существует точка X вне прямой
таких точек нет. Предположим, что существует точка X вне прямой
![]() , принадлежащая каждой окружности. Тогда
, принадлежащая каждой окружности. Тогда ![]() X =
X = ![]() и . В
треугольнике
и . В
треугольнике ![]() X =
X = ![]() длина стороны
длина стороны ![]() равна сумме длин сторон
равна сумме длин сторон![]() X и
X и ![]() X, что
невозможно.
X, что
невозможно.
4) Докажем, что окружности касаются внешним
образом. Таким образом, либо точка F лежит вне окружности ω1(![]() ,
, ![]() ), когда
), когда ![]() F <
F < ![]() , либо эта точка принадлежит обеим окружностям, если
, либо эта точка принадлежит обеим окружностям, если ![]() F = R1. Но в
этом случае точка F есть точка A касания окружностей. Следовательно, окружность ω2(
F = R1. Но в
этом случае точка F есть точка A касания окружностей. Следовательно, окружность ω2(![]() ,
, ![]() ) рас-
положена вне части плоскости, ограниченной окружностью ω1(
) рас-
положена вне части плоскости, ограниченной окружностью ω1(![]() ,
, ![]() ). Аналогично можно доказать, что окружность ω1(
). Аналогично можно доказать, что окружность ω1(![]() ,
, ![]() ) расположена вне части плоскости, ограниченной
окружностью ω2(
) расположена вне части плоскости, ограниченной
окружностью ω2(![]() ,
, ![]() ). Теперь доказано, что окружности ω1(
). Теперь доказано, что окружности ω1(![]() ,
, ![]() ) и ω2(
) и ω2(![]() ,
, ![]() ) касаются
внешним образом.
) касаются
внешним образом.
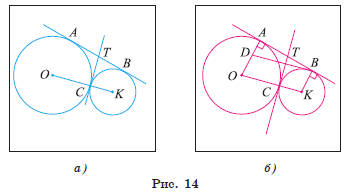
Задача 3. Две окружности с центрами в точках O и K, радиусы которых равны 16 см и 9 см соответственно, касаются внешним образом в точке C. К окружностям проведена общая касательная AB, где точки A и B — точки касания. Общая касательная, проведенная через точку C, пересекает касательную AB в точке T (рис. 14, а). Вычислите длину отрезка CT.
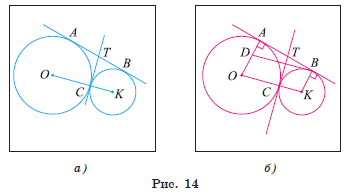
Решение.
Для решения задачи воспользуемся тем, что отрезки касательных, проведенные к окружности из одной точки, равны, а радиусы, проведенные в точку касания, перпендикулярны касательной. Учтем также, что окружности касаются внешним образом, а значит, расстояние между их центрам равно сумме их радиусов.
1) Так как отрезки касательных к
окружности, проведенные из одной точки, равны, то TC = TA = TB, т. e . ![]() .
.
2) Так как окружности касаются внешним образом, то OK = OC + CK = 16 + 9 = 25 (см).
3) Рассмотрим четырехугольник ODBK. Пусть D ∈ OA и BD ⃦ OK (рис. 14, б). Так как радиус, проведенный в точку касания,
перпендикулярен касательной, то ∠
BAD = 90°, т. е.
треугольник BAD — прямоугольный. Следовательно, AB = ![]() .
.
4) Четырехугольник ODBK —
параллелограмм, так как его противолежащие стороны параллельны, значит, DB = OK = 25 см. Кроме того, DA = OA − OD = OA − KB = 16 − 9 = 7 (см). Тогда AB
=![]() тогда
тогда ![]() .
.
Ответ: 12 см.
Определение . Центральным углом окружности называется угол с вершиной в центре этой окружности.
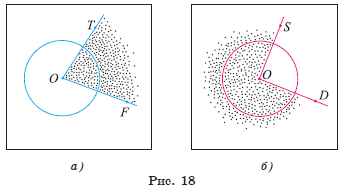
Например, на рисунке 18, а изображен центральный угол TOF, который меньше развернутого угла, а на рисунке 18, б — центральный угол SOD — больше развернутого угла.
Любые две различные точки A и В окружности служат концами двух дуг. Для различия этих дуг на каждой из них отмечается некоторая промежуточная точка. Например, если на дугах отмечены точки F и T, то в этом случае дуги обозначаются ∪ATB и ∪ AFB и данная запись читается так: «дуга ATB и дуга AFB» (рис. 19, а). Если понятно, о какой из двух дуг идет речь, употребляется также обозначение ∪AB.
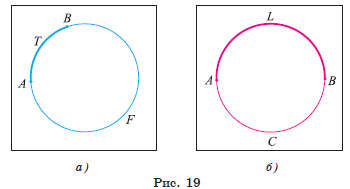
Дуга AB окружности называется полуокружностью, если ее концы служат концами диаметра этой окружности. Например, на рисунке 19, б изображены полуокружности
ALB и ACB.
Пусть точки A и B не являются концами диаметра окружности с центром в точке O. Тогда лучи OA и OB служат сторонами двух центральных углов, один из которых меньше, а другой больше развернутого угла (рис. 20, а).
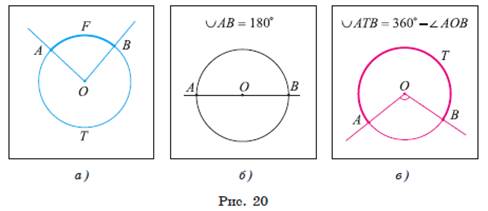
Дуга AB окружности ω(O, R) и центральный угол AOB, внутри которого лежит эта дуга, называются соответствующими.
Если дуга окружности лежит внутри соответствующего ей центрального угла, который меньше развернутого угла, то говорят, что эта дуга меньше полуокружности.
Если дуга окружности лежит внутри соответствующего ей центрального угла, который больше развернутого угла, то говорят, что дуга больше полуокружности.
Например, на рисунке 20, а изображены дуга AFB, которая меньше полуокружности, и дуга ATB — больше полуокружности.
Для сравнения дуг окружности вводится понятие градусной меры дуги окружности.
Дадим определение градусной меры дуги окружности.
Определение. Градусной мерой дуги окружности называется градусная мера соответствующего ей центрального угла.
Градусная мера дуги AB, как и сама дуга, обозначается ∪AB.
Таким образом, если дуга AB окружности меньше полуокружности, а ∠ AOB — соответствующий ей центральный угол, то ∪AB = ∠AOB (см. рис 20, а).
Если дуга AB является полуокружностью, то ее градусная мера равна 180° (рис. 20, б).
Градусная мера дуги ATB, которая больше полуокружности и дополняет дугу AB, меньшую полуокружности, до окружности, равна 360° − ∠ AOB, где угол AOB соответствует дуге AB (рис. 20, в).
Понятие градусной меры дуги позволяет определить понятие равенства дуг окружности.
Две дуги одной и той же окружности называются равными, если равны их градусные меры.
Если градусная мера дуги AB равна 33°, то пишут ∪AB = 33°. Читают: «Градусная мера дуги AB равна 33°», или крат ко «Дуга AB равна 33°».
Рассмотрим примеры. Пусть диагонали квадрата ABCD пересекаются в точке O. Окружность ω(C, CO) пересекает стороны BC и CD квадрата в точках F и L соответственно. Тогда ∪FOL = 90° , а градусная мера дуги FO, которая меньше полуокружности, равна 45°. Градусная мера дуги FLO, которая больше полуокружности, равна 360° − ∠ FCO = 360° − 45° = 315° (рис. 21, а).
Рассмотрим еще один пример. Пусть точка O — центр окружности, отрезок AB — хорда окружности, равная ее радиусу, а отрезок AC — диаметр окружности (рис. 21, б).
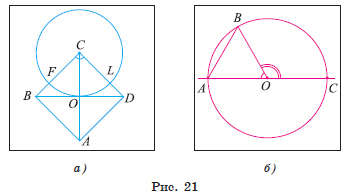
Тогда градусная мера дуги AB, которая меньше полуокружности, равна 60°, так как треугольник AOB — равносторонний, а значит, градусная мера соответствующего ей центрального угла AOB равна 60°. Градусная мера дуги BC, которая меньше полуокружности, равна 120°, так как градусная мера соответствующего ей центрального угла BOC равна 120°.
Можем вычислить градусную меру дуги BAC, которая больше полуокружности: ∪BAC= 360° − ∠ BOC = 360° − 120° = 240°.
Определение. Угол называется вписанным в окружность, если он меньше развернутого угла, вершина его лежит на окружности, а стороны пересекают эту окружность.
Например, на рисунке 22, а изображен вписанный угол TOF. Если точки A, B и С лежат на окружности, то каждый из углов ABC, BCA, CAB является вписанным (рис. 22, б).
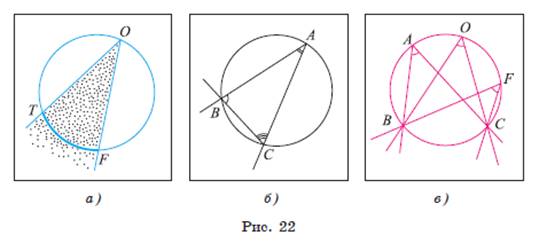
Пусть ∠ TOF — вписанный угол, при этом T и F — точки пересечения его сторон с окружностью, а TF — дуга, которая лежит внутри этого вписанного угла. В этом случае говорят, что вписанный угол TOF опирается на дугу TF (см. рис. 22, а).
Например, на рисунке 22, в изображены вписанные углы BAC, BOC и BFC, которые опираются на одну и ту же дугу BC.
Теперь докажем теорему о вписанном угле.
Теорема 1 (о вписанном угле). Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.
Доказательство.
Пусть вписанный в окружность ω(O, R) угол ABC опирается
на дугу AC. Докажем, что ∠ABC
= ![]() ∪ AC.
Рассмотрим три возможных случая. Центр O окружности лежит: 1) на одной из сторон угла; 2) во
внутренней области угла; 3) во внешней области угла.
∪ AC.
Рассмотрим три возможных случая. Центр O окружности лежит: 1) на одной из сторон угла; 2) во
внутренней области угла; 3) во внешней области угла.
Первый случай. Центр O окружности лежит на одной из сторон угла ABC, например на стороне BC (рис. 23).

1) Дуга AC меньше полуокружности, следовательно, ∪AC = ∠AOC.
2) Угол AOC — внешний угол равнобедренного треугольника AOB, значит, ∠AOC = ∠1+ ∠2.
3) Так как углы при основании
равнобедренного треугольника AOB равны, то ∠
2 =
=![]() ∠AOC.
∠AOC.
4) Так как ∠ABC = ∠2 = ![]() ∠AOC и ∠AOC = ∪AC, то ∠ABC =
∠AOC и ∠AOC = ∪AC, то ∠ABC = ![]() ∪ AC.
∪ AC.
Второй случай. Центр O окружности лежит во внутренней области угла.
1) Пусть D — точка пересечения луча BO и дуги AC (рис. 24).
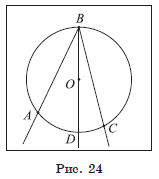
Тогда по доказанному в первом случае ∠ABD = ![]() ∪ AD
и ∠DBC =
∪ AD
и ∠DBC = ![]() ∪ DC.
∪ DC.
2) ∠
ABC =
∠ ABD +
∠ DBC =
![]() ∪ AD +
∪ AD + ![]() ∪ DC =
∪ DC = ![]() (∪AD +
∪DC)
=
(∪AD +
∪DC)
= ![]() ∪ AC.
∪ AC.
Таким образом, ∠ABC = ![]() ∪ AC.
∪ AC.
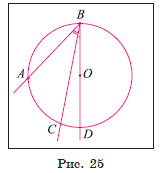
Третий случай. Центр O окружности лежит во внешней области угла ABC.
1) Пусть D — точка пересечения луча BO с
окружностью (рис. 25). Тогда согласно доказанному в первом случае ∠ABD = ![]() ∪ AD и ∠CBD =
∪ AD и ∠CBD = ![]() ∪ CD.
∪ CD.
2) ∠ ABC = ∠ABD − ∠CBD =![]() (∪AD − ∪CD) =
(∪AD − ∪CD) =![]() ∪ AC.
∪ AC.
Таким образом, ∠ABC
= ![]() ∪ AC
∪ AC
Теорема доказана.
Из данной теоремы получим следующие следствия.
Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 26, а).
Следствие 2. Вписанный угол, опирающийся на полуокружность, прямой (рис. 26, б).
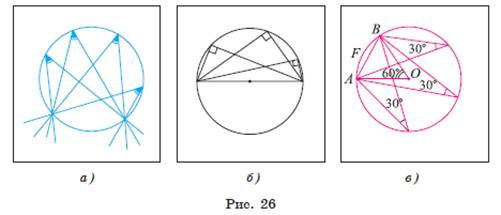
Рассмотрим пример. Пусть хорда AB соединяет
концы дуги AFB и равна радиусу окружности ω(O, R). Тогда
градусная мера каждого из вписанных углов, опирающихся на дугу AFB, равна
30° (рис.
26, в). Действительно, градусная мера центрального угла AOB равна 60°, значит, ∪AFB = 60°. Каждый из указанных углов опирается на дуга AFB,
следовательно, градусная мера каждого из них равна ![]() ∪ AFB = 30°.
∪ AFB = 30°.
Теорема 2 (об угле между хордой и касательной). Градусная мера угла, сторонами которого служат касательная и хорда, равна половине градусной меры дуги, расположенной внутри этого угла.
Д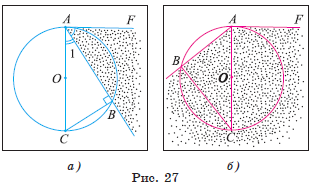 ано: ω(O, R),
ано: ω(O, R),
AF — касательная,
AB — хорда.
Доказать:
∠FAB = ![]() ∪ AB.
∪ AB.
Доказательство.
Первый случай. Пусть угол FAB — острый (рис. 27, а).
1) Проведем диаметр AC. Тогда вписанный угол CBA опирается на полуокружность, значит, по следствию 2 он прямой, т. е. ∠ CBA = 90°.
2) Треугольник CBA — прямоугольный, следовательно, ∠ACB = 90° − ∠1.
3) Так как диаметр AC перпендикулярен
касательной FA, то ∠ FAB = 90° − ∠ 1. Таким
образом, ∠ FAB = ∠ ACB. Так как
вписанный угол ACB опирается на дугу AB, то ∠ACB= =![]() ∪ AB.
∪ AB.
Следовательно, ∠FAB = ![]() ∪ AB.
∪ AB.
Второй случай. Пусть угол FAB — тупой (рис. 27, б).
Проведем диаметр CA. Тогда
∠FAB = ∠BAC + ∠CAF = ![]() ∪ BC +
∪ BC + ![]() ∪ CA =
∪ CA =![]() (∪BC + ∪CA) =
(∪BC + ∪CA) = ![]() ∪ BCA,
∪ BCA,
но дуга BCA лежит внутри тупого угла FAB.
Теорема доказана.
Теорема 3 (об отрезках пересекающихся хорд). Если две хорды окружности пересекаются, то произведение длин отрезков одной хорды равно произведению длин отрезков другой хорды.
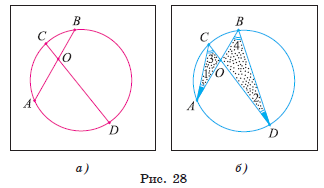
Д а н о:
AB, CD — хорды окружности,
O = AB ∩ CD (рис. 28, а).
Д о к а з а т ь:
AO * OB = CO * OD.
Доказательство.
1) Проведем хорды AC и BD (рис. 28, б). Рассмотрим треугольники AOC и DOB.
2) Заметим, что ∠ 1 = ∠ 2, так как они вписанные и опираются на одну и ту же дугу CB. Кроме того, ∠ 3 = ∠ 4, так как они вписанные и опираются на одну и ту же дугу AD.
3) Треугольник AOC подобен треугольнику DOB по первому признаку подобия треугольников, так как ∠ 1 = ∠ 2 и ∠ 3 = ∠ 4.
4) Из подобия треугольников AOC и DOB следует, что
![]()
Значит,
![]()
Теорема доказана.
Пусть через точку S, лежащую вне окружности, проведена секущая, которая пересекает окружность в точках С и В, и SC < SB.
Тогда отрезок SB называется отрезком секущей, а отрезок SC — ее внешней частью.
Теорема 4 (об отрезках секущей и касательной). Если через точку, лежащую вне круга, ограниченного окружностью, провести к этой окружности касательную и секущую, то квадрат длины отрезка касательной равен произведению длин отрезков секущей и ее внешней части.

Д а н о: ω(O, R),
SA — касательная, SB — секущая, SC внешняя часть секущей (рис. 29, а).
Доказать: ![]()
Доказательство.
1) Проведем хорды AC и AB (рис. 29, б).
2) По теореме о вписанном угле ∠ABC = ![]() ∪AC. Кроме того, в силу теоремы 2 имеем ∠SAC =
∪AC. Кроме того, в силу теоремы 2 имеем ∠SAC = ![]() ∪ AC. Значит, ∠ ABC = ∠ SAC.
∪ AC. Значит, ∠ ABC = ∠ SAC.
3) Так как ∠ ABC = ∠ SAC и ∠ 1 — общий угол треугольников ASB и CSA, то эти треугольники подобны.
4) Из подобия треугольников ASB и CSA следует,
что выполняется равенство ![]() или
или ![]()
Теорема доказана.
Из данной теоремы получим следствие.
Следствие. Если через точку S, лежащую вне круга, ограниченного
окружностью, проведены две секущие, пересекающие окружность соответственно в
точках ![]() , (рис. 30, a).
, (рис. 30, a).
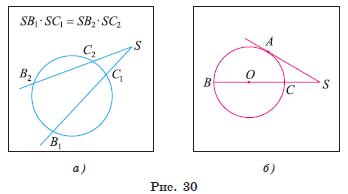
Задача 1. Через точку S проведена секущая, которая про- ходит через центр O окружности ω(O, R) и пересекает ее в точках C и B, SC : CB = 1 : 2. Найдите длину отрезка SA касательной (рис. 30, б).
Решение.
По теореме об отрезках секущей и
касательной имеем ![]() Так как SC : CB = =1 : 2, а CB = 2R, то SC = R и SB = SC + CB = 3R. Тогда
Так как SC : CB = =1 : 2, а CB = 2R, то SC = R и SB = SC + CB = 3R. Тогда ![]() =
3R
* R =
=
3R
* R = ![]() Отсюда
Отсюда ![]()
От в е т: SA = ![]()
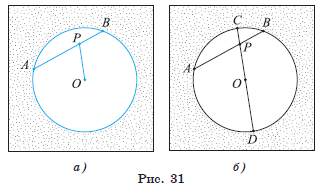
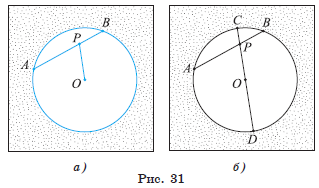
Задача 2. Радиус круга равен 7,5 см. Точка P лежит внутри круга на расстоянии 6,5 см от его центра O. Через точку P проведена хорда AB, длина которой равна 9 см. Вычислите длины отрезков, на которые точка P делит хорду AB.
Д а н о: ω(O, R),
R = 7,5 см,
P ∈ AB,
PO = 6,5 см,
AB = 9 см.
Н а й т и:
BP и AP.
Решение.
Воспользуемся теоремой об отрезках пересекающихся хорд.
1) Пусть C и D — точки пересечения прямой OP с границей круга (рис. 31, б). Тогда CO = OD = 7,5 см.
2) По теореме об отрезках пересекающихся хорд имеем AP * PB = CP * PD, или PB(9 − - PB) = CP * PD.
3) Заметим, что CP = CO − PO= 7,5 − 6,5 = 1 (см). Кроме того, PD = PO + OD = 7,5 + 6,5 = 14 (см). Таким образом,(9 − PB) * PB = 14. Отсюда найдем: PB = 2 см или PB = 7 см. Следовательно, PB = 2 см и AP = 7 см или PB = 7 см и AP = 2 см.
Ответ: 2 см, 7 см.
Ранее мы уже отмечали следующие свойства: медианы треугольника пересекаются в одной точке; биссектрисы треугольника пересекаются в одной точке; высоты треугольника, или прямые, их содержащие, пересекаются в одной точке.
Теорема о свойстве медиан треугольника была доказана в восьмом классе. Сейчас докажем теоремы о свойствах биссектрис и высот треугольника.
Предварительно докажем одно свойство биссектрисы угла.
Теорема 1 (о свойстве биссектрисы угла). Каждая точка биссектрисы угла, который меньше развернутого, равноудалена от его сторон. Каждая точка указанного угла, равноудаленная от его сторон, лежит на биссектрисе этого угла.
Доказательство.
I. Докажем, что каждая точка биссектрисы угла, который меньше развернутого угла, равноудалена от его сторон.
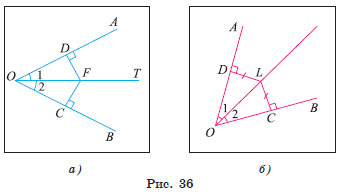
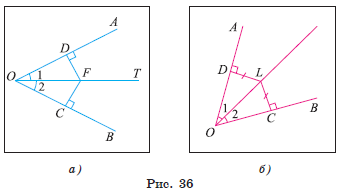
1) Пусть луч OT — биссектриса угла AOB, т. е. ∠ 1 = ∠ 2, а F — произвольная точка биссектрисы OT. Проведем перпендикуляры FC и FD к прямым BO и AO соответственно и докажем, что FC = FD (рис. 36, а).
2) Рассмотрим прямоугольные треугольники OFD и OFC. Эти треугольники равны по гипотенузе и острому углу (отрезок OF — общая гипотенуза, ∠ 1 = ∠ 2).
3) Из равенства треугольников OFD и OFC следует, что FC = FD.
Что и требовалось доказать.
II. Докажем, что если точка равноудалена от сторон угла, который меньше развернутого угла, то она лежит на его биссектрисе.
1) Пусть точка L равноудалена от сторон угла AOB, т. е. перпендикуляры LD и LC, проведенные к сторонам угла, равны. Докажем, что луч OL — биссектриса угла AOB (рис. 36, б).
2) Рассмотрим прямоугольные треугольники ODL и OCL. Эти треугольники равны по гипотенузе и катету (отрезок OL — общая гипотенуза, LD = LC).
3) Из равенства треугольников ODL и OCL следует, что ∠ 1 = ∠ 2, т. е. луч OL — биссектриса угла AOB.
Что и требовалось доказать.
Теорема 2 (о точке пересечения биссектрис). Биссектрисы треугольника пересекаются в одной точке.
Доказательство.
1) Пусть отрезки ![]() и
и ![]() —биссектрисы треугольника ABC.
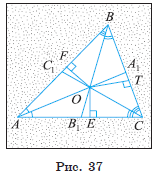
Докажем, что они пересекаются в одной точке (рис. 37).
—биссектрисы треугольника ABC.
Докажем, что они пересекаются в одной точке (рис. 37).
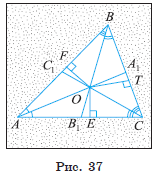
Пусть O — точка пересечения
биссектрис ![]() отрезки OF, OT и OE — перпендикуляры, проведенные из точки O к прямым AB, BC и AC
соответственно.
отрезки OF, OT и OE — перпендикуляры, проведенные из точки O к прямым AB, BC и AC
соответственно.
2) Так как луч AO является биссектрисой угла BAC, то по теореме о свойстве биссектрисы угла выполняется равенство OE = OF. Так как луч BO — биссектриса угла ABC, то OF = OT также по теореме о свойстве биссектрисы угла.
Отсюда следует, что OE = OT.
3) Равенство OE = OT означает,
что точка O равноудалена от сторон угла ACB. Следовательно,
по теореме о свойстве биссектрисы угла получим, что точка O лежит на биссектрисе
угла ACB. Иначе говоря, биссектриса CC1 проходит
через точку O. Таким образом, все три биссектрисы![]() и
и ![]() треугольника ABC
пересекаются в точке O.
треугольника ABC
пересекаются в точке O.
Теорема доказана.
Воспользуемся этими свойствами для доказательства следующей теоремы.
Теорема 3 (о точке пересечения серединных перпендикуляров к сторонам треугольника). Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Доказательство.
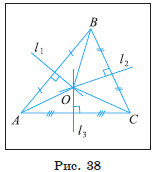
Пусть ![]() и
и ![]() - серединные перпендикуляры к сторонам AB, BC и AC треугольника
ABC соответственно (рис. 38).
- серединные перпендикуляры к сторонам AB, BC и AC треугольника
ABC соответственно (рис. 38).
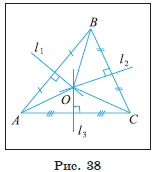
Докажем, что серединные перпендикуляры ![]() и
и ![]() пересекаются в одной точке.
пересекаются в одной точке.
1) Пусть O — точка пересечения
серединных перпендикуляров![]() . Тогда по теореме о серединном перпендикуляре
справедливы равенства OA = OB (так как прямая — серединный перпендикуляр к отрезку AB) и OB = OC (так как
прямая
. Тогда по теореме о серединном перпендикуляре
справедливы равенства OA = OB (так как прямая — серединный перпендикуляр к отрезку AB) и OB = OC (так как
прямая ![]() — серединный перпендикуляр к отрезку BC). Отсюда
следует, что OA = OC.
— серединный перпендикуляр к отрезку BC). Отсюда
следует, что OA = OC.
2) Равенство OA = OC означает,
что точка O равно удалена от вершин A и C. Значит,
по теореме о серединном перпендикуляре точка O лежит на серединном
перпендикуляре к стороне AC. Таким образом, все три серединных перпендикуляра ![]() и
и ![]() пересекаются в одной точке.
пересекаются в одной точке.
Теорема доказана.
Воспользуемся теоремой 3 для доказательства свойства высот треугольника.
Теорема 4 (о точке пересечения прямых, на которых лежат высоты треугольника). Прямые, на которых лежат высоты треугольника, пересекаются в одной точке.
Доказательство.
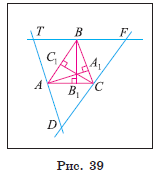
1) Пусть отрезки ![]() и
и ![]() — высоты произвольного треугольника ABC (рис.
39). Докажем, что прямые, содержащие высоты треугольника, пересекаются в одной
точке.
— высоты произвольного треугольника ABC (рис.
39). Докажем, что прямые, содержащие высоты треугольника, пересекаются в одной
точке.
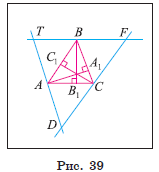
2) Проведем через вершины A, B и C прямые, параллельные сторонам BC, AC и AB соответственно. Пусть T, F и D — точки их пересечения.
3) Докажем, что точки A, B и C являются соответственно серединами сторон TD, TF и FD треугольника TFD. Например, докажем, что точка C — середина стороны DF. Так как четырехугольник ABCD — параллелограмм, то AB = DC. Так как ABFC — параллелограмм, то AB = CF. Таким образом, DC = CF.
4) Аналогично доказывается, что AT = AD и TB = BF. По условию AA1 ⊥ BC, а по построению TD ⃦ BC, следовательно,
![]() ⊥ TD.
Аналогично
⊥ TD.
Аналогично ![]() ⊥ TF и CC1 ⊥ DF. Значит, прямые
⊥ TF и CC1 ⊥ DF. Значит, прямые ![]() и
и ![]() являются серединными перпендикулярами к сторонам
треугольника TFD. Следовательно, они пересекаются в одной точке.
являются серединными перпендикулярами к сторонам
треугольника TFD. Следовательно, они пересекаются в одной точке.
Теорема доказана.
Точка пересечения медиан, точка пересечения биссектрис и точка пересечения прямых, содержащих высоты треугольника, называются замечательными точками треугольника.
Заметим, что если треугольник остроугольный, то пересекаются в одной точке сами его высоты, а если треугольник тупоугольный, то пересекаются в одной точке прямые, содержащие высоты.
Определение. Окружность называется вписанной в треугольник, если она касается всех сторон треугольника. В этом случае треугольник называется описанным около окружности.
Например, на рисунке 44, а изображена окружность, вписанная в треугольник ABC. Окружность, которая изображена на рисунке 44, б не является вписанной в треугольник ABC, так как она не касается стороны BC
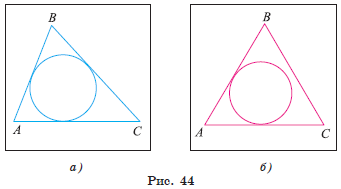
Круг называется вписанным в треугольник, если его граница вписана в этот треугольник.
Следующая теорема дает ответ на вопрос о существовании окружности, вписанной в треугольник.
Теорема 1 (о существовании окружности, вписанной в треугольник). В любой треугольник можно вписать единственную окружность.
Доказательство.
I. Докажем, что в треугольник можно вписать окружность.
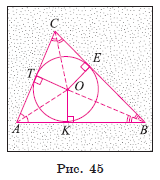
1) Пусть O — точка пересечения биссектрис произвольного треугольника ABC (рис.45).
.
2) Отрезки OK, OE и OT — перпендикуляры, проведенные из точки O к сторонам AB, BC и AC соответственно.
3) По теореме о биссектрисе угла точка O равноудалена от сторон треугольника, следовательно, OK = OE = OT. Таким образом, окружность с центром в точке O и радиусом, равным отрезку OK, проходит через точки K, E и T.
4) Стороны AB, BC и AC треугольника касаются этой окружности в точках K, E и T, так как они перпендикулярны радиусам OK, OE и OT соответственно. Следовательно, окружность с центром в точке O и радиусом OK является вписанной в треугольник ABC. Существование вписанной окружности доказано.
II. Докажем, что такая окружность единственная.
Допустим, что в треугольник можно вписать две окружности. Тогда центр каждой из окружностей равноудален от сторон треугольника, а следовательно, совпадает с точкой O пересечения биссектрис треугольника; ее радиус равен расстоянию от точки O до сторон треугольника. Таким образом, эти окружности совпадают. Теорема доказана.
Определение. Окружность называется описанной около треугольника, если все его вершины лежат на этой окружности. В этом случае треугольник называется вписанным в окружность.
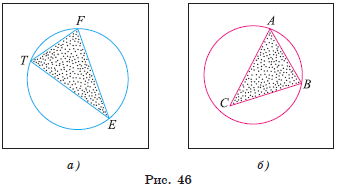
Например, на рисунке 46, а изображена окружность, которая является описанной около треугольника TFE. Окружность, которая изображена на рисунке 46, б, не является описанной около треугольника ABC, так как вершина C не лежит на окружности.
Круг называется описанным около треугольника, если его граница описана около этого треугольника.
Докажем теорему о существовании описанной около треугольника окружности.
Теорема 2 (о существовании окружности, описанной около треугольника). Около любого треугольника можно описать единственную окружность.
Доказательство.
I. Докажем, что около треугольника можно описать окружность.
1) Пусть O — точка пересечения серединных перпендикуляров к сторонам произвольного треугольника ABC (рис. 47).
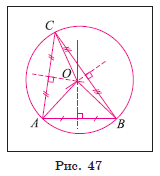
2) Так как точки серединного перпендикуляра к отрезку равноудалены от его концов, то OA = OB = OC. Таким образом, окружность с центром в точке O и радиусом, равным отрезку OA, проходит через все вершины треугольника ABC, а значит, является описанной около этого треугольника.
II. Докажем, что такая окружность единственная.
Предположим, что около треугольника можно описать еще одну окружность. Тогда ее центр равноудален от вершин треугольника, а следовательно, совпадает с точкой O пересечения серединных перпендикуляров к сторонам треугольника; ее радиус равен расстоянию от точки O до вершин треугольника.
Таким образом, окружности совпадают. Теорема доказана.
Задача 1. Докажите, что радиус r вписанной в прямоугольный треугольник окружности можно найти по формуле r = p − c, где p — полупериметр прямоугольного треугольника, c длины отрезков, на которые точка P делит хорду AB.
Д а н о: ω(O, R),
R = 7,5 см,
P ∈ AB,
PO = 6,5 см,
AB = 9 см.
Н а й т и:
BP и AP.
Доказательство.
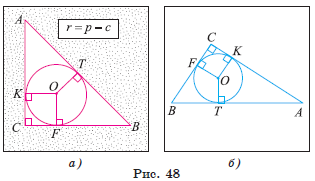
1) Пусть K, T, F — точки касания вписанной окружности соответственно со сторонами AС, AB и BC треугольника ABC, точка O — центр этой окружности (рис. 48, а, б). Четырехугольник CKOF — квадрат (т. к. ∠ OKC = ∠ KCF = ∠ CFO = 90°, CK = CF), значит, CF = CK = OK = OF = r.
2) Отрезки касательных, проведенные из одной точки, равны, следовательно, AT = AK = AC − r и BT = BF = BC − r.
3) Так как AT
+ BT = c, то (AC − r) + (BC − r) = c. Таким образом, ![]() или
или ![]() .
.
Что и требовалось доказать.
Определение. Окружность называется вписанной в четырехугольник, если она касается всех сторон четырехугольника. В этом случае четырехугольник называется описанным около окружности.
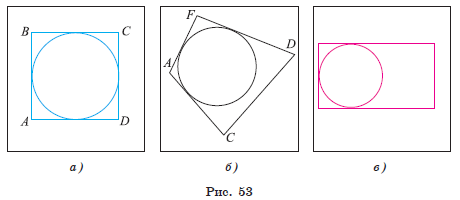
Например, на рисунке 53, а изображены квадрат ABCD и вписанная в него окружность. Окружность, изображенная на рисунке 53, б, не является вписанной в четырехугольник AFDC, так как она не касается его стороны DC.
Заметим, что не в любой четырехугольник можно вписать окружность. Например, в прямоугольник, не являющийся квадратом, нельзя вписать окружность. Существует окружность, которая касается трех сторон такого прямоугольника, и не существует окружности, касающейся всех его четырех сторон (рис. 53, в).
Круг называется вписанным в четырехугольник, если его граница вписана в четырехугольник.
Следующая теорема характеризует свойство четырехугольника, в который можно вписать окружность.
Теорема 1 (о свойстве четырехугольника, в который можно вписать окружность). Если в четырехугольник можно вписать окружность, то суммы длин его противолежащих сторон равны.
Доказательство.
1) Пусть в четырехугольник ABCD вписана окружность, которая касается его сторон в точках F, O, T и E (рис. 54).
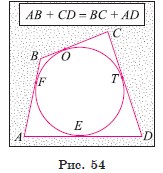
Докажем, что AB + CD = BC + AD.
2) Так как отрезки касательных к окружности, проведенные из одной точки, равны, то AF = AE = a, BF = BO = b, CO = CT = m, DT = DE = c.
3) Таким образом, AB + CD = (AF + FB) + (CT + DT) = a + b + c + m и BC + AD = (BO + +OC) + (AE + ED) = a + b + c + m. Отсюда следует, что AB + CD = BC + AD.
Теорема доказана.
Справедливо и обратное утверждение, которое отвечает на вопрос, при каком условии в четырехугольник можно вписать окружность.
Теорема 2 (условие, при котором в четырехугольник можно вписать окружность). Если в выпуклом четырехугольнике суммы длин противолежащих сторон равны, то в этот четырехугольник можно вписать окружность.
Доказательство.
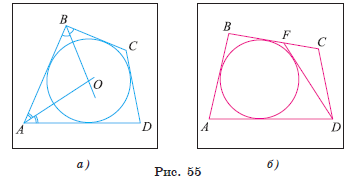
1) Пусть ABCD — выпуклый четырехугольник, в котором AB + CD = BC + AD. Докажем, что в этот четырехугольник можно вписать окружность.
2) Рассмотрим окружность, которая касается трех сторон: AB, BC и AD. Центр O этой окружности есть точка пересечения биссектрис углов CBA и BAD (рис. 55, а).
3) Докажем, что эта окружность вписана в четырехугольник, т. е. что она касается также и стороны CD. Предположим, что это не так. Тогда либо сторона CD не пересекает окружность, либо является секущей.
4) Пусть сторона CD не пересекает окружность (рис. 55, б). Проведем касательную DF, где F ∈ BC. Так как ABFD — описанный четырехугольник, то верно равенство AB + DF = = AD + BF. Кроме того, по условию AB + CD = BF + FC + AD. Отсюда следует, что AB + CD = AB + DF + FC или CD = DF + FC, что невозможно, так как в треугольнике DFC длина стороны CD должна быть меньше суммы длин двух других сторон. Аналогично приводит к противоречию и предположение о том, что сторона CD является секущей.
5) Таким образом, предположение о том, что сторона CD не касается рассматриваемой окружности, неверно. Следовательно, сторона CD касается этой окружности, и, значит, окружность вписана в четырехугольник ABCD. Теорема доказана.
Определение. Окружность называется описанной около четырехугольника, если все его вершины лежат на окружности. В этом случае четырехугольник называется вписанным в окружность.
Круг называется описанным около четырехугольника, если его граница описана около четырехугольника.
Теперь рассмотрим свойство четырехугольника, вписанного в окружность.
Теорема3 (о свойстве четырехугольника, вписанного в окружность). Если около четырехугольника описана окружность, то суммы градусных мер его противолежащих углов равны 180°.
Доказательство.
1) Пусть четырехугольник ABCD вписан в окружность (рис. 56).
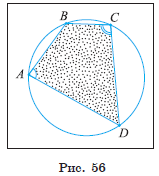
Докажем, что ∠ A + ∠ C = 180° и ∠ B + ∠ D = 180°.
2) Так как углы A и C —
вписанные, то ∠A = ![]() ∪ BCD и ∠C =
∪ BCD и ∠C = ![]() ∪ BAD.
∪ BAD.
Значит, ∠
A +
∠ C =
![]() ∪ BCD +
∪ BCD + ![]() ∪ BAD =
∪ BAD =![]() (∪BCD + ∪BAD) =
(∪BCD + ∪BAD) =![]() * 360°=180°.
* 360°=180°.
Так как сумма градусных мер углов четырехугольника ABCD равна 360° и ∠ A + ∠ C = =180°, то ∠ B + ∠ D = 180°.
Теорема доказана.
Справедливо и обратное утверждение, которое характеризует условие, при котором около четырехугольника можно описать окружность.
Теорема 4 (условие, при котором около четырехугольника можно описать окружность). Если в четырехугольнике суммы градусных мер противолежащих углов равны 180°, то около такого четырехугольника можно описать окружность.
Доказательство.
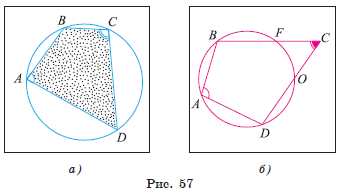
1) Пусть в четырехугольнике ABCD выполняется равенство ∠ A + ∠ C = 180°. Докажем, что около четырехугольника ABCD можно описать окружность (рис. 57, а).
2) Рассмотрим окружность, описанную около треугольника ABD, и докажем, что эта окружность проходит также через вершину C. Предположим, что окружность не проходит через вершину C. Тогда либо вершина C лежит вне круга, границей которого служит рассматриваемая окружность, либо внутри этого круга.
3) Пусть вершина C лежит вне круга
(рис. 57, б). Обозначим буквами F и O точки пересечения
сторон BC и DC с окружностью. Тогда ∠C = ![]() (∪DAB − ∪FO). Следовательно,
(∪DAB − ∪FO). Следовательно,
∠ С < ![]() ∪ DAB. Так как угол A
является вписанным, то ∠ A =
∪ DAB. Так как угол A
является вписанным, то ∠ A = ![]() ∪BOD. Тогда ∠ A + ∠ C <
<
∪BOD. Тогда ∠ A + ∠ C <
<![]() (∪BOD + ∪DAB) <
(∪BOD + ∪DAB) <![]() = 180°.
= 180°.
Это противоречит условию, значит, наше предположение неверно, т. е. окружность проходит через вершину С. Аналогично можно доказать, что вершина С не может лежать внутри круга.
Теорема доказана.
Из доказанной теоремы следует, что около любого прямоугольника можно описать окружность.
Рассмотрим некоторые задачу, при решении которой используются доказанные теоремы.
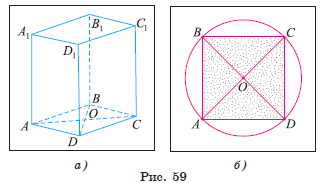
Задача. Основанием прямоугольного параллелепипеда ![]() является квадрат. Вычислите площадь боковой грани
параллелепипеда, если диаметр окружности, описанной около основания
параллелепипеда, равен
является квадрат. Вычислите площадь боковой грани
параллелепипеда, если диаметр окружности, описанной около основания
параллелепипеда, равен ![]() см, боковое ребро в два раза больше стороны основания.
см, боковое ребро в два раза больше стороны основания.
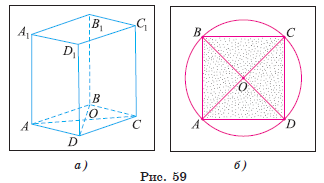
Решение.
Каждая грань прямоугольного
параллелепипеда является прямоугольником. Так как основания параллелепипеда —
квадраты, то боковые грани — равные прямоугольники. Площадь прямоугольника
равна произведению длин его сторон, следовательно, достаточно вычислить, например,
длины отрезков DC и ![]() , тогда площадь грани
, тогда площадь грани ![]() (рис. 59, а).
(рис. 59, а).
1) Диагональ квадрата, вписанного в
окружность, равна диаметру окружности, значит, AC =![]() см (рис. 59, б).
см (рис. 59, б).
2) В равнобедренном прямоугольном треугольнике ADC имеем DC = 3 см.
3) По условию боковое ребро
параллелепипеда в два раза больше стороны основания. Значит,![]() = 2DC = 6 см.
= 2DC = 6 см.
4) Теперь вычислим площадь боковой грани ![]() = 18.
= 18.
Задача. Через точку A, находящуюся от центра O окружности на расстоянии 10 см, проведены две касательные AB и AC, где B и С — точки касания. Вычислите площадь SABOC четырехугольника ABOC, если AB + AC == 16 см ( рис. 7).
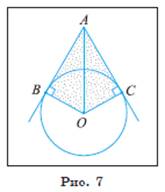
Решение.
1) Площадь четырехугольника ABOC равна сумме площадей треугольников ABO и ACO.
2) По свойству касательной ∠ OBA = ∠ OCA = 90°. Прямоугольные треугольники ABO и ACO равны по
гипотенузе и катету (AO — общая, OB = OC). Значит,![]()
3) Отрезки касательных к окружности, проведенные из одной точки, равны. Следовательно, AB = AC = 8 см. Теперь, применив теорему Пифагора, вычислим
![]()
Таким образом, ![]()
Ответ: ![]() .
.
Задача. Точка F — середина основания BC равнобедренного треугольника ABC. Докажите, что прямая BC является касательной к окружности ω(A, AF) (рис. 8, а, б).
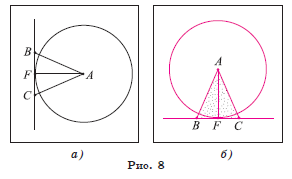
Доказательство.
1) Прямая BC проходит через конец F радиуса окружности ω(A, AF). Для доказательства того, что BC является касательной, достаточно доказать, что BC ⊥ AF.
2) В равнобедренном треугольнике ABC отрезок AF — медиана, проведенная к его основанию. Следовательно, AF ⊥ BC. Таким образом, по признаку касательной прямая BC касается окружности ω(A, AF).
Что и требовалось доказать.
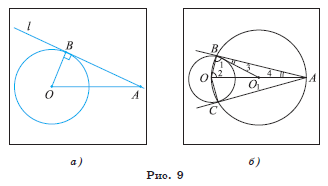
Задача. Точка A лежит вне окружности ω(O, R). Постройте прямую, которая касается окружности и проходит через точку A.
Поиск решения.
1) Пусть прямая l, проходящая через точку A и касающаяся окружности ω(O, R), построена. Точка B — точка касания. Тогда по свойству касательной OB ⊥ AB (рис. 9, а). Следовательно, для построения искомой касательной необходимо построить точку B на окружности ω(O, R) так, что OB ⊥ AB.
2) Рассмотрим окружность ω1,
диаметром которой является отрезок AO, т. е. ![]() Пусть B и C — точки
пересечения окружностей ω(O, R) и
Пусть B и C — точки
пересечения окружностей ω(O, R) и ![]() (рис. 9, б). Заметим, что ∠
1 =
∠ 2 и ∠ 3 = ∠ 4, как углы при основании равнобедренных
треугольников
(рис. 9, б). Заметим, что ∠
1 =
∠ 2 и ∠ 3 = ∠ 4, как углы при основании равнобедренных
треугольников ![]() и
и ![]() соответственно.
Так как ∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 = 180°, то ∠ 1 + ∠ 3 = ∠ 2 + ∠ 4 = 90°. Значит, ∠ OBA = 90°, т. е. OB ⊥
AB. Аналогично
доказывается, что OC ⊥ AC. Отсюда по признаку касательной к окружности
следует, что прямые AB и AC являются касательными. Теперь понятна
последовательность необходимых построений.
соответственно.
Так как ∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 = 180°, то ∠ 1 + ∠ 3 = ∠ 2 + ∠ 4 = 90°. Значит, ∠ OBA = 90°, т. е. OB ⊥
AB. Аналогично
доказывается, что OC ⊥ AC. Отсюда по признаку касательной к окружности
следует, что прямые AB и AC являются касательными. Теперь понятна
последовательность необходимых построений.
Построение.
1) Проводим отрезок OA, соединяющий центр О данной окружности и точку A (рис10,а).
2) Строим середину O1 отрезка OA: O FE OA 1 = ∩ .
Точки F и E — точки пересечения окружностей ω2(O, r) и ω3(A, r), где ![]() (рис. 10, б).
(рис. 10, б).
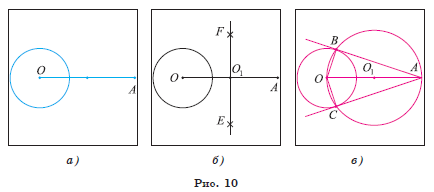
3) Строим окружность ω1(O1, O1A) (рис. 10, в) и точки B, C — точки пересечения данной и построенной окружностей.
4) Прямые AB и AC — искомые касательные к данной окружности.
Доказательство.
По построению ∠OBA = 90° и ∠OCA = 90° (см. задачу № 251 учебного пособия «Геометрия, 7»), т. е. AB ⊥ OB и AC ⊥ OB. Следовательно, по признаку касательной AB и AC — касательные.
Задача. Докажите, что если две окружности ![]() касаются внешним образом, то расстояние между их
центрами равно сумме их радиусов, т. е.
касаются внешним образом, то расстояние между их
центрами равно сумме их радиусов, т. е. ![]() .
.
Доказательство.
1) Пусть окружности![]() касаются
внешним образом в точке A (рис. 13, а).
касаются
внешним образом в точке A (рис. 13, а).
2) Докажем, что точка A лежит на
отрезке ![]() . Допустим, что точка A не лежит
на отрезке
. Допустим, что точка A не лежит
на отрезке ![]() . Заметим, что в случае внешнего касания точка A не может
лежать на продолжении отрезка
. Заметим, что в случае внешнего касания точка A не может
лежать на продолжении отрезка ![]() . Пусть точка касания A не лежит
на отрезке
. Пусть точка касания A не лежит
на отрезке ![]() (рис. 13, б). Тогда
(рис. 13, б). Тогда ![]() A =
A =
![]() и
и ![]() A =
A =
![]()
3) Пусть F — точка, симметричная точке
A относительно прямой ![]() . Окружности
. Окружности![]() имеют две общие точки, что противоречит условию их
касания. Следовательно, точка касания A
лежит на отрезке
имеют две общие точки, что противоречит условию их
касания. Следовательно, точка касания A
лежит на отрезке ![]() .
.
4) Докажем, что ![]() . Точка A лежит на отрезке
. Точка A лежит на отрезке ![]() , значит,
, значит, ![]() .
.
Теорема доказана.
Справедливо и обратное утверждение.
Задача. Докажите, если расстояние между центрами двух окружностей, лежащих в плоскости, равно сумме их радиусов, то такие окружности касаются внешним образом.
Доказательство.
1) Пусть даны две окружности ![]() и известно, что
и известно, что ![]() . Докажем, что окружности касаются внешним образом.
. Докажем, что окружности касаются внешним образом.
2) На отрезке ![]() рассмотрим точку A такую, что
рассмотрим точку A такую, что ![]() A =
A = ![]() . Тогда
. Тогда ![]() A =
A =
![]() −
− ![]() A = (
A = (![]() +
+ ![]() ) −
) − ![]() =
= ![]() . Таким
. Таким
образом, точка A принадлежит каждой из данных окружностей.
3) Докажем,
что окружности не имеют других общих точек. Действительно, на прямой ![]() таких точек нет. Предположим, что существует точка X вне прямой
таких точек нет. Предположим, что существует точка X вне прямой
![]() , принадлежащая каждой окружности. Тогда
, принадлежащая каждой окружности. Тогда ![]() X =
X = ![]() и . В
треугольнике
и . В
треугольнике ![]() X =
X = ![]() длина стороны
длина стороны ![]() равна сумме длин сторон
равна сумме длин сторон![]() X и
X и ![]() X, что
невозможно.
X, что
невозможно.
4) Докажем, что окружности касаются внешним
образом. Таким образом, либо точка F лежит вне окружности ω1(![]() ,
, ![]() ), когда
), когда ![]() F <
F < ![]() , либо эта точка принадлежит обеим окружностям, если
, либо эта точка принадлежит обеим окружностям, если ![]() F = R1. Но в
этом случае точка F есть точка A касания окружностей. Следовательно, окружность ω2(
F = R1. Но в
этом случае точка F есть точка A касания окружностей. Следовательно, окружность ω2(![]() ,
, ![]() ) рас-
положена вне части плоскости, ограниченной окружностью ω1(
) рас-
положена вне части плоскости, ограниченной окружностью ω1(![]() ,
, ![]() ). Аналогично можно доказать, что окружность ω1(
). Аналогично можно доказать, что окружность ω1(![]() ,
, ![]() ) расположена вне части плоскости, ограниченной
окружностью ω2(
) расположена вне части плоскости, ограниченной
окружностью ω2(![]() ,
, ![]() ). Теперь доказано, что окружности ω1(
). Теперь доказано, что окружности ω1(![]() ,
, ![]() ) и ω2(
) и ω2(![]() ,
, ![]() ) касаются
внешним образом.
) касаются
внешним образом.
Задача. Две окружности с центрами в точках O и K, радиусы которых равны 16 см и 9 см соответственно, касаются внешним образом в точке C. К окружностям проведена общая касательная AB, где точки A и B — точки касания. Общая касательная, проведенная через точку C, пересекает касательную AB в точке T (рис. 14, а). Вычислите длину отрезка CT.
Решение.
Для решения задачи воспользуемся тем, что отрезки касательных, проведенные к окружности из одной точки, равны, а радиусы, проведенные в точку касания, перпендикулярны касательной. Учтем также, что окружности касаются внешним образом, а значит, расстояние между их центрам равно сумме их радиусов.
1) Так как отрезки касательных к
окружности, проведенные из одной точки, равны, то TC = TA = TB, т. e . ![]() .
.
2) Так как окружности касаются внешним образом, то OK = OC + CK = 16 + 9 = 25 (см).
3) Рассмотрим четырехугольник ODBK. Пусть D ∈ OA и BD ⃦ OK (рис. 14, б). Так как радиус, проведенный в точку касания,
перпендикулярен касательной, то ∠
BAD = 90°, т. е.
треугольник BAD — прямоугольный. Следовательно, AB = ![]() .
.
4) Четырехугольник ODBK —
параллелограмм, так как его противолежащие стороны параллельны, значит, DB = OK = 25 см. Кроме того, DA = OA − OD = OA − KB = 16 − 9 = 7 (см). Тогда AB
=![]() тогда
тогда ![]() .
.
Ответ: 12 см.
Задача . Через точку S проведена секущая, которая про- ходит через центр O окружности ω(O, R) и пересекает ее в точках C и B, SC : CB = 1 : 2. Найдите длину отрезка SA касательной (рис. 30, б).
Решение.
По теореме об отрезках секущей и
касательной имеем ![]() Так как SC : CB = =1 : 2, а CB = 2R, то SC = R и SB = SC + CB = 3R. Тогда
Так как SC : CB = =1 : 2, а CB = 2R, то SC = R и SB = SC + CB = 3R. Тогда ![]() =
3R
* R =
=
3R
* R = ![]() Отсюда
Отсюда ![]()
От в е т: SA = ![]()
Задача Радиус круга равен 7,5 см. Точка P лежит внутри круга на расстоянии 6,5 см от его центра O. Через точку P проведена хорда AB, длина которой равна 9 см. Вычислите длины отрезков, на которые точка P делит хорду AB.
Д а н о: ω(O, R),
R = 7,5 см,
P ∈ AB,
PO = 6,5 см,
AB = 9 см.
Н а й т и:
BP и AP.
Решение.
Воспользуемся теоремой об отрезках пересекающихся хорд.
1) Пусть C и D — точки пересечения прямой OP с границей круга (рис. 31, б). Тогда CO = OD = 7,5 см.
2) По теореме об отрезках пересекающихся хорд имеем AP * PB = CP * PD, или PB(9 − - PB) = CP * PD.
3) Заметим, что CP = CO − PO= 7,5 − 6,5 = 1 (см). Кроме того, PD = PO + OD = 7,5 + 6,5 = 14 (см). Таким образом,(9 − PB) * PB = 14. Отсюда найдем: PB = 2 см или PB = 7 см. Следовательно, PB = 2 см и AP = 7 см или PB = 7 см и AP = 2 см.
Ответ: 2 см, 7 см.
Теорема 1 (о свойстве биссектрисы угла). Каждая точка биссектрисы угла, который меньше развернутого, равноудалена от его сторон. Каждая точка указанного угла, равноудаленная от его сторон, лежит на биссектрисе этого угла.
Доказательство.
I. Докажем, что каждая точка биссектрисы угла, который меньше развернутого угла, равноудалена от его сторон.
1) Пусть луч OT — биссектриса угла AOB, т. е. ∠ 1 = ∠ 2, а F — произвольная точка биссектрисы OT. Проведем перпендикуляры FC и FD к прямым BO и AO соответственно и докажем, что FC = FD (рис. 36, а).
2) Рассмотрим прямоугольные треугольники OFD и OFC. Эти треугольники равны по гипотенузе и острому углу (отрезок OF — общая гипотенуза, ∠ 1 = ∠ 2).
3) Из равенства треугольников OFD и OFC следует, что FC = FD.
Что и требовалось доказать.
II. Докажем, что если точка равноудалена от сторон угла, который меньше развернутого угла, то она лежит на его биссектрисе.
1) Пусть точка L равноудалена от сторон угла AOB, т. е. перпендикуляры LD и LC, проведенные к сторонам угла, равны. Докажем, что луч OL — биссектриса угла AOB (рис. 36, б).
2) Рассмотрим прямоугольные треугольники ODL и OCL. Эти треугольники равны по гипотенузе и катету (отрезок OL — общая гипотенуза, LD = LC).
3) Из равенства треугольников ODL и OCL следует, что ∠ 1 = ∠ 2, т. е. луч OL — биссектриса угла AOB.
Что и требовалось доказать.
Теорема 2 (о точке пересечения биссектрис). Биссектрисы треугольника пересекаются в одной точке.
Доказательство.
1) Пусть отрезки ![]() и
и ![]() —биссектрисы треугольника ABC.
Докажем, что они пересекаются в одной точке (рис. 37).
—биссектрисы треугольника ABC.
Докажем, что они пересекаются в одной точке (рис. 37).
Пусть O — точка пересечения
биссектрис ![]() отрезки OF, OT и OE — перпендикуляры, проведенные из точки O к прямым AB, BC и AC
соответственно.
отрезки OF, OT и OE — перпендикуляры, проведенные из точки O к прямым AB, BC и AC
соответственно.
2) Так как луч AO является биссектрисой угла BAC, то по теореме о свойстве биссектрисы угла выполняется равенство OE = OF. Так как луч BO — биссектриса угла ABC, то OF = OT также по теореме о свойстве биссектрисы угла.
Отсюда следует, что OE = OT.
3) Равенство OE = OT означает,
что точка O равноудалена от сторон угла ACB.
Следовательно, по теореме о свойстве биссектрисы угла получим, что точка O лежит на
биссектрисе угла ACB. Иначе говоря, биссектриса CC1 проходит
через точку O. Таким образом, все три биссектрисы![]() и
и ![]() треугольника ABC
пересекаются в точке O.
треугольника ABC
пересекаются в точке O.
Теорема доказана.
Теорема 3 (о точке пересечения серединных перпендикуляров к сторонам треугольника). Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Доказательство.
Пусть ![]() и
и ![]() - серединные перпендикуляры к сторонам AB, BC и AC треугольника
ABC соответственно (рис. 38).
- серединные перпендикуляры к сторонам AB, BC и AC треугольника
ABC соответственно (рис. 38).
Докажем, что серединные перпендикуляры ![]() и
и ![]() пересекаются в одной точке.
пересекаются в одной точке.
1) Пусть O — точка пересечения
серединных перпендикуляров![]() . Тогда по теореме о серединном перпендикуляре
справедливы равенства OA = OB (так как прямая — серединный перпендикуляр к отрезку AB) и OB = OC (так как
прямая
. Тогда по теореме о серединном перпендикуляре
справедливы равенства OA = OB (так как прямая — серединный перпендикуляр к отрезку AB) и OB = OC (так как
прямая ![]() — серединный перпендикуляр к отрезку BC). Отсюда
следует, что OA = OC.
— серединный перпендикуляр к отрезку BC). Отсюда
следует, что OA = OC.
2) Равенство OA = OC означает,
что точка O равно удалена от вершин A и C. Значит,
по теореме о серединном перпендикуляре точка O лежит на серединном
перпендикуляре к стороне AC. Таким образом, все три серединных перпендикуляра ![]() и
и ![]() пересекаются в одной точке.
пересекаются в одной точке.
Теорема доказана.
Воспользуемся теоремой 3 для доказательства свойства высот треугольника.
Теорема 4 (о точке пересечения прямых, на которых лежат высоты треугольника). Прямые, на которых лежат высоты треугольника, пересекаются в одной точке.
Доказательство.
1) Пусть отрезки ![]() и
и ![]() — высоты произвольного треугольника ABC (рис.
39). Докажем, что прямые, содержащие высоты треугольника, пересекаются в одной
точке.
— высоты произвольного треугольника ABC (рис.
39). Докажем, что прямые, содержащие высоты треугольника, пересекаются в одной
точке.
2) Проведем через вершины A, B и C прямые, параллельные сторонам BC, AC и AB соответственно. Пусть T, F и D — точки их пересечения.
3) Докажем, что точки A, B и C являются соответственно серединами сторон TD, TF и FD треугольника TFD. Например, докажем, что точка C — середина стороны DF. Так как четырехугольник ABCD — параллелограмм, то AB = DC. Так как ABFC — параллелограмм, то AB = CF. Таким образом, DC = CF.
4) Аналогично доказывается, что AT = AD и TB = BF. По условию AA1 ⊥ BC, а по построению TD ⃦ BC, следовательно,
![]() ⊥ TD.
Аналогично
⊥ TD.
Аналогично ![]() ⊥ TF и CC1 ⊥ DF. Значит, прямые
⊥ TF и CC1 ⊥ DF. Значит, прямые ![]() и
и ![]() являются серединными перпендикулярами к сторонам
треугольника TFD. Следовательно, они пересекаются в одной точке.
являются серединными перпендикулярами к сторонам
треугольника TFD. Следовательно, они пересекаются в одной точке.
Теорема доказана.
Точка пересечения медиан, точка пересечения биссектрис и точка пересечения прямых, содержащих высоты треугольника, называются замечательными точками треугольника.
Заметим, что если треугольник остроугольный, то пересекаются в одной точке сами его высоты, а если треугольник тупоугольный, то пересекаются в одной точке прямые, содержащие высоты.
Задача. Докажите, что радиус r вписанной в прямоугольный треугольник окружности можно найти по формуле r = p − c, где p — полупериметр прямоугольного треугольника, c длины отрезков, на которые точка P делит хорду AB.
![]()
Д а н о: ω(O, R),
R = 7,5 см,
P ∈ AB,
PO = 6,5 см,
AB = 9 см.
Н а й т и:
BP и AP.
Доказательство.
1) Пусть K, T, F — точки касания вписанной окружности соответственно со сторонами AС, AB и BC треугольника ABC, точка O — центр этой окружности (рис. 48, а, б). Четырехугольник CKOF — квадрат (т. к. ∠ OKC = ∠ KCF = ∠ CFO = 90°, CK = CF), значит, CF = CK = OK = OF = r.
2) Отрезки касательных, проведенные из одной точки, равны, следовательно, AT = AK = AC − r и BT = BF = BC − r.
3) Так как AT
+ BT = c, то (AC − r) + (BC − r) = c. Таким образом, ![]() или
или ![]() .
.
Что и требовалось доказать.
Задача. Основанием прямоугольного параллелепипеда ![]() является квадрат. Вычислите площадь боковой грани
параллелепипеда, если диаметр окружности, описанной около основания
параллелепипеда, равен
является квадрат. Вычислите площадь боковой грани
параллелепипеда, если диаметр окружности, описанной около основания
параллелепипеда, равен ![]() см, боковое ребро в два раза больше стороны
основания.
см, боковое ребро в два раза больше стороны
основания.
Решение.
Каждая грань прямоугольного
параллелепипеда является прямоугольником. Так как основания параллелепипеда —
квадраты, то боковые грани — равные прямоугольники. Площадь прямоугольника
равна произведению длин его сторон, следовательно, достаточно вычислить,
например, длины отрезков DC и ![]() , тогда площадь грани
, тогда площадь грани ![]() (рис. 59, а).
(рис. 59, а).
1) Диагональ квадрата, вписанного в
окружность, равна диаметру окружности, значит, AC =![]() см (рис. 59, б).
см (рис. 59, б).
2) В равнобедренном прямоугольном треугольнике ADC имеем DC = 3 см.
3) По условию боковое ребро
параллелепипеда в два раза больше стороны основания. Значит,![]() = 2DC = 6 см.
= 2DC = 6 см.
4) Теперь вычислим площадь боковой грани ![]() = 18.
= 18.
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
Самостоятельная работа №1
«Вписанные и описанные многоугольники»
Вариант 1
1. Вычислите радианные меры углов треугольника, если они пропорциональны числам 4, 5, 9.
2. Вычислите длину окружности, описанной около прямоугольника со сторонами 15см и 8см.
3. Около правильного треугольника со стороной 5 см описана окружность. Найдите: а) радиус описанной окружности; б) сторону правильного шестиугольника, вписанного в эту же окружность.
4. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см. Найдите: а) радиус данной окружности; б) длину одной из медиан треугольника АВС
Вариант 2
1. Найдите радианную меру углов треугольника АВС если его угол А равен 120°, угол С 18°.
2. В правильный четырёхугольник со стороной 4 см вписана окружность. Найдите: а) радиус окружности; б) сторону правильного треугольника, описанного около данной окружности.
3. Вычислите длину окружности, описанной около прямоугольного треугольника с катетами 20см и 15см.
4. Диаметры окружности АС и ВD пересекаются под углом 90.Длина дуги ВС равна 4π см. Найдите: а) радиус данной окружности; б) длины хорд с концами в точках A, B, C, D.
Самостоятельная работа № 2
«Вписанные и описанные многоугольники »
Вариант 1
1. Вычислите радианные меры углов треугольника, если они пропорциональны числам 4, 5, 9.
2. . Вычислите длину окружности, описанной около прямоугольника со сторонами 15см и 8см.
3. Около правильного треугольника со стороной 5 см описана окружность. Найдите: а) радиус описанной окружности; б)сторону правильного шестиугольника, вписанного в эту же окружность.
4. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см. Найдите: а) радиус данной окружности; б) длину одной из медиан треугольника АВС
Вариант 2
1. Найдите радианную меру углов треугольника АВС если его угол А равен 120°, угол С 18°.
2. В правильный четырёхугольник со стороной 4 см вписана окружность. Найдите: а) радиус окружности; б) сторону правильного треугольника, описанного около данной окружности.
3. Вычислите длину окружности, описанной около прямоугольного треугольника с катетами 20см и 15см.
4. Диаметры окружности АС и ВD пересекаются под углом 90.Длина дуги ВС равна 4π см. Найдите: а) радиус данной окружности; б) длины хорд с концами в точках A, B, C, D.
КОНТРОЛЬНЫЕ РАБОТЫ
Контрольная работа № 1
«Вписанные и описанные многоугольники»
Вариант 1
![]() №1. Окружность
касается сторон квадрата ABCD в точках K, P, T, O (см. рисунок слева). Выпишите:
№1. Окружность
касается сторон квадрата ABCD в точках K, P, T, O (см. рисунок слева). Выпишите:
1) четырёхугольник, описанный около окружности;
2) четырёхугольник, вписанный в окружность;
3) два треугольника, вписанных в окружность
№2. Точки T и P лежат соответственно на сторонах AB и BC квадрата ABCD, угол TPC равен 135°. Поясните, можно ли около
четырёхугольника ATPC описать окружность?
№3. Длина стороны квадрата ABCD равна 4 см. Точка T лежит на стороне CD и CT = 1 см.
Вычислите длину радиуса окружности, вписанной в треугольник ATD.
№4. В прямоугольнике ABCD AB = 4 см, BC = 5 см. Точка P – внутренняя точка отрезка BC. В четырёхугольник APDC вписана окружность. Вычислите расстояние от центра окружности до точки A.
№5. В равнобедренный треугольник ABC (AB = BC) вписана окружность. Касательная l к
окружности, параллельна прямой AC, пересекает стороны AB и BC в точках T и P соответственно. Известно, что периметр четырёхугольника ATPC равен 30 см и AC = 12 см. Вычислите длину радиуса окружности.
Вариант 2
![]()
№1. Окружность касается сторон треугольника ABC в точках E, T и O (см.рисунок слева). Выпишите:
1) треугольник, описанный около окружности;
2) четырёхугольник, вписанный в окружность;
3) два треугольника, вписанных в окружность
№2. Точки T и O лежат соответственно на сторонах AB и BC
равностороннего треугольника ABC, угол TOC равен 120°. Поясните, можно ли около четырёхугольника ATOC описать окружность?
№3. Длина стороны квадрата ABCD равна 8 см. Точка O лежит на стороне BC и BO:OC = 3:1. Вычислите длину радиуса окружности, вписанной в треугольник ABO.
№4. В прямоугольнике ABCD BC = 10 см. Точка T – внутренняя точка отрезка BC. В
четырёхугольник ATCD вписана окружность. Известно, что длина радиуса окружности равна 4 см. Вычислите расстояние от центра окружности до точки A.
№5. В равнобедренный треугольник ABC (AC = CB) вписана окружность. Касательная l к
окружности, параллельная прямой AB, пересекает стороны AC и BC в точках O и P соответственно. Известно, что AC = 5 см, Ab = 6 см. Вычислите периметр четырёхугольника AOPB.
Вариант 3
![]() №1. Окружность
касается сторон квадрата ABCD в точках K, P, T, O (см. рисунок слева). Выпишите:
№1. Окружность
касается сторон квадрата ABCD в точках K, P, T, O (см. рисунок слева). Выпишите:
1) четырёхугольник, описанный около окружности;
2) четырёхугольник, вписанный в окружность;
3) два треугольника, вписанных в окружность
№2. Точки T и P лежат соответственно на сторонах AB и BC квадрата ABCD, угол TPC равен 126°. Поясните, можно ли около
четырёхугольника ATPC описать окружность?
№3. Длина стороны квадрата ABCD равна 8 см. Точка T лежит на стороне CD и CT = 1 см.
Вычислите длину радиуса окружности, вписанной в треугольник ATD.
№4. В прямоугольнике ABCD AB = 3 см, BC = 4 см. Точка P – внутренняя точка отрезка BC. В четырёхугольник APDC вписана окружность. Вычислите расстояние от центра окружности до точки A.
№5. В равнобедренный треугольник ABC (AB = BC) вписана окружность. Касательная l к
окружности, параллельна прямой AC, пересекает стороны AB и BC в точках T и P соответственно. Известно, что периметр четырёхугольника ATPC равен 35 см и AC = 15 см. Вычислите длину радиуса окружности.
Вариант 4
![]()
№1. Окружность касается сторон треугольника ABC в точках E, T и O (см. рисунок слева). Выпишите:
1) треугольник, описанный около окружности;
2) четырёхугольник, вписанный в окружность;
3) два треугольника, вписанных в окружность
№2. Точки T и O лежат соответственно на сторонах AB и BC
равностороннего треугольника ABC, угол TOC равен 140°. Поясните, можно ли около четырёхугольника ATOC описать окружность?
№3. Длина стороны квадрата ABCD равна 6 см. Точка O лежит на стороне BC и BO:OC = 3:1. Вычислите длину радиуса окружности, вписанной в треугольник ABO.
№4. В прямоугольнике ABCD BC = 14 см. Точка T – внутренняя точка отрезка BC. В
четырёхугольник ATCD вписана окружность. Известно, что длина радиуса окружности равна 4 см. Вычислите расстояние от центра окружности до точки A.
№5. В равнобедренный треугольник ABC (AC = CB) вписана окружность. Касательная l к
окружности, параллельная прямой AB, пересекает стороны AC и BC в точках O и P соответственно. Известно, что AC = 7 см, Ab = 8 см. Вычислите периметр четырёхугольника AOPB.
Контрольная работа № 2
«Касательная к окружности. Центральные и вписанные углы»
Вариант 1
1. Изобразите прямую и окружность, имеющие две общие точки
2. Вписанный угол равен 76°. Найдите центральный угол, соответствующий данному вписанному углу.
3. Диаметр окружности равен 5 см. На окружности лежит точка, расстояние от которой до одного из концов диаметра равно 3 см. Найдите расстояние от точки до второго конца диаметра.
4. Хорды AB и CD окружности пересекаются в точке F, которая является серединой AB. Вычислите длину хорды AB, если CD=13 см, FC=4 см.
5. Две окружности касаются внешним образом в точке А. Радиус одной окружности равен 1 см. Общая касательная к этим окружностям проходит через точку А и пересекает другую их общую касательную в точке В. Вычислите радиус другой окружности, если длина отрезка АВ равна 3 см.
Вариант 2
1. Изобразите прямую и окружность, имеющие только одну общую точку
2. Центральный угол равен 128°. Найдите вписанный угол, соответствующий данному центральному углу.
3. На окружности взята точка. Расстояния от точки до концов диаметра равны 5 см и 12 см. Найдите радиус окружности.
4. Хорды AB и CD окружности пересекаются в точке F, которая является серединой AB. Вычислите длину хорды AB, если CD=10 см, FC=2 см.
5. Две окружности касаются внешним образом в точке А. Радиус одной окружности равен 3 см. Общая касательная к этим окружностям проходит через точку А и пересекает другую их общую касательную в точке В. Вычислите радиус другой окружности, если длина отрезка АВ равна 6 см.
Вариант 3
1. Изобразите прямую и окружность, имеющие две общие точки
2. Вписанный угол равен 66°. Найдите центральный угол, соответствующий данному вписанному углу.
3. Диаметр окружности равен 8 см. На окружности лежит точка, расстояние от которой до одного из концов диаметра равно 5 см. Найдите расстояние от точки до второго конца диаметра.
4. Хорды AB и CD окружности пересекаются в точке F, которая является серединой AB. Вычислите длину хорды AB, если CD=15 см, FC=6 см.
5. Две окружности касаются внешним образом в точке А. Радиус одной окружности равен 3 см. Общая касательная к этим окружностям проходит через точку А, и пересекает другую их общую касательную в точке В. Вычислите радиус другой окружности, если длина отрезка АВ равна 5 см.
Вариант 4
1. Изобразите прямую и окружность, имеющие только одну общую точку
2. Центральный угол равен 138°. Найдите вписанный угол, соответствующий данному центральному углу.
3. На окружности взята точка. Расстояния от точки до концов диаметра равны 8 см и 16 см. Найдите радиус окружности.
4. Хорды AB и CD окружности пересекаются в точке F, которая является серединой AB. Вычислите длину хорды AB, если CD=16 см, FC=5 см.
5. Две окружности касаются внешним образом в точке А. Радиус одной окружности равен 2 см. Общая касательная к этим окружностям проходит через точку А, и пересекает другую, их общую касательную в точке В. Вычислите радиус другой окружности, если длина отрезка АВ равна 6 см.
План-конспект урока по теме:
«Вписанные и описанные четырехугольники»
Обучающая цель урока: Применение различных формул при решении задач по теме «Вписанные и описанные многоугольники»
Тип урока: Закрепление нового материала.
Задачи личностного развития:
1. Развитие логического мышления учащихся.
2. Организация ситуации для саморегулирования учащихся на прогнозируемый результат познавательной деятельности.
3.
Содействие развитию у учащихся
самостоятельности и творческих способностей.
Ход урока:
I.Организационно – мотивационный этап.
Цель этапа (ожидаемый результат): создание психологической готовности класса к уроку, введение учащихся в атмосферу познавательной деятельности.
Педагогическая задача: способствовать установлению эмоционально позитивного настроения учащихся, подготовить их к плодотворной работе.
|
Деятельность учителя |
Деятельность учащихся |
|
Организую доброжелательный настрой учащихся. Отмечаю отсутствующих. |
Эмоционально настраиваются на работу, определяют свое настроение |
II. Контролирующий этап: проверка домашнего
задания.
Цель этапа: осознание учащимися результативности своей деятельности, уровня усвоения учебного материала
Педагогическая задача: выяснить степень усвоения знаний учащихся, стимулировать к овладению приемами учения и самообразования
|
Деятельность учителя |
Деятельность учащихся |
|
Учащимся задаются вопросы: 1) с какими трудностями вы столкнулись при выполнении домашнего задания? 2) на что нужно обратить внимание при решении данных уравнений? |
Проверяют домашнее задание, задают вопросы, отвечают на вопросы. |
III. Актуализация знаний, целеполагание.
Цель этапа: подготовка учащихся к сознательному освоению учебного материала, повторение предыдущего материала, вопросов для обсуждения и его конечного результата, мотивация на познавательную деятельность.
|
Деятельность учителя |
Деятельность учащихся |
|
1) Дать определение описанной окружности. |
Окружность называется описанной около многоугольника, если все его вершины лежат на этой окружности. При этом многоугольник называется вписанным в окружность |
|
2) ) Дать определение вписанной окружности.
|
Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности. |
IV. Этап усвоения новых знаний.
Цель этапа: поиск необходимой информации; самостоятельное планирование исследований, развитие умений делать выводы.
Педагогическая задача: способствовать формированию умений планировать свою деятельность, выделять нужную информацию, анализировать, обобщать.
|
Деятельность учителя |
Деятельность учащихся |
|
Решить: 1.Квадрат ABCD описан около окружности, центром которой является точка O (рис. 60, а). Вычислите площадь треугольника COB, если радиус окружности равен 2 см.
2. Прямоугольная трапеция ABCD описана около окружности. Вычислите длину большей боковой стороны, если радиус окружности равен 4 см, а градусная мера острого угла трапеции равна 60° (рис. 60, б).
3.Около окружности описана равнобедренная трапеция, периметр которой равен 12 см. Вычислите длину боковой стороны трапеции. 4. В равнобедренную трапецию вписана окружность. Вычислите длину средней линии трапеции, если длина боковой стороны трапеции равна 4 см. |
Решают у доски и на месте. 1. 2.
3.
4.
|
V. Подведение итогов и рефлексия.
Цель этапа: осознание учащимися результативности своей деятельности на уроке, уровня усвоения учебного материала
Педагогическая задача: организовать условия для формулирования учащимися основ по учебной теме и оценивания своих собственных достижений.
|
Деятельность учителя |
Деятельность учащихся |
|
Предлагается вспомнить поставленные в начале урока цели и задачи и сделать вывод Учитель просит оценить свою работу в листе самооценки и ответить на вопросы: · какой способ работы над темой для тебя оказался самым продуктивным? -как вы считаете, какие из поставленных целей в начале урока нам удалось достичь? · определите одну из причин, которая не дала вам возможность повысить отметку · что надо сделать для улучшения результатов? |
Анализируют степень достижения поставленных целей, участвуют в подведении итогов урока. |
VI. Домашнее задание.
Педагогическая задача: подготовить учащихся к выполнению домашнего задания, предложить решить задание творческого характера.
|
Деятельность учителя |
Деятельность учащихся |
|
Домашнее задание : №159, №157. |
Записывают домашнее задание. |
Л
План-конспект урока по теме:
«Замечательные точки треугольника»
Обучающая цель урока: Применение различных формул при решении задач по теме «Замечательные точки треугольника»
Тип урока: Изучение нового материала.
Задачи личностного развития:
4. Развитие логического мышления учащихся.
5. Организация ситуации для саморегулирования учащихся на прогнозируемый результат познавательной деятельности.
6.
Содействие развитию у учащихся
самостоятельности и творческих способностей.
Ход урока:
II. Организационно – мотивационный этап.
Цель этапа (ожидаемый результат): создание психологической готовности класса к уроку, введение учащихся в атмосферу познавательной деятельности.
Педагогическая задача: способствовать установлению эмоционально позитивного настроения учащихся, подготовить их к плодотворной работе.
|
Деятельность учителя |
Деятельность учащихся |
|
Организую доброжелательный настрой учащихся. Отмечаю отсутствующих. |
Эмоционально настраиваются на работу, определяют свое настроение |
II. Контролирующий этап: проверка домашнего
задания.
Цель этапа: осознание учащимися результативности своей деятельности, уровня усвоения учебного материала
Педагогическая задача: выяснить степень усвоения знаний учащихся, стимулировать к овладению приемами учения и самообразования
|
Деятельность учителя |
Деятельность учащихся |
|
Учащимся задаются вопросы: 3) с какими трудностями вы столкнулись при выполнении домашнего задания? 4) на что нужно обратить внимание при решении данных уравнений? |
Проверяют домашнее задание, задают вопросы, отвечают на вопросы. |
III. Актуализация знаний, целеполагание.
Цель этапа: подготовка учащихся к сознательному освоению учебного материала, повторение предыдущего материала, вопросов для обсуждения и его конечного результата, мотивация на познавательную деятельность.
|
Деятельность учителя |
Деятельность учащихся |
|
Ранее мы уже отмечали следующие свойства: медианы треугольника пересекаются в одной точке; биссектрисы треугольника пересекаются в одной точке; высоты треугольника, или прямые, их содержащие, пересекаются в одной точке. Теорема о свойстве медиан треугольника была доказана в восьмом классе. Сейчас докажем теоремы о свойствах биссектрис и высот треугольника. 1.Теорема о точке пересечения биссектрис треугольника.Предварительно докажем одно свойство биссектрисы угла. Теорема 1 (о свойстве биссектрисы угла). Каждая точка биссектрисы угла, который меньше развернутого, равноудалена от его сторон. Каждая точка указанного угла, равноудаленная от его сторон, лежит на биссектрисе этого угла.
Доказательство. I. Докажем, что каждая точка биссектрисы угла, который меньше развернутого угла, равноудалена от его сторон. 1) Пусть луч OT — биссектриса угла AOB, т. е. ∠ 1 = ∠ 2, а F — произвольная точка биссектрисы OT. Проведем перпендикуляры FC и FD к прямым BO и AO соответственно и докажем, что FC = FD (рис. 36, а). 2) Рассмотрим прямоугольные треугольники OFD и OFC. Эти треугольники равны по гипотенузе и острому углу (отрезок OF — общая гипотенуза, ∠ 1 = ∠ 2). 3) Из равенства треугольников OFD и OFC следует, что FC = FD. Что и требовалось доказать. II. Докажем, что если точка равноудалена от сторон угла, который меньше развернутого угла, то она лежит на его биссектрисе. 1) Пусть точка L равноудалена от сторон угла AOB, т. е. перпендикуляры LD и LC, проведенные к сторонам угла, равны. Докажем, что луч OL — биссектриса угла AOB (рис. 36, б). 2) Рассмотрим прямоугольные треугольники ODL и OCL. Эти треугольники равны по гипотенузе и катету (отрезок OL — общая гипотенуза, LD = LC). 3) Из равенства треугольников ODL и OCL следует, что ∠ 1 = ∠ 2, т. е. луч OL — биссектриса угла AOB. Что и требовалось доказать. Теорема 2 (о точке пересечения биссектрис). Биссектрисы треугольника пересекаются в одной точке. Доказательство. 1) Пусть отрезки
Пусть O — точка пересечения
биссектрис 2) Так как луч AO является биссектрисой угла BAC, то по теореме о свойстве биссектрисы угла выполняется равенство OE = OF. Так как луч BO — биссектриса угла ABC, то OF = OT также по теореме о свойстве биссектрисы угла. Отсюда следует, что OE = OT. 3) Равенство OE = OT означает,
что точка O равноудалена от сторон угла ACB.
Следовательно, по теореме о свойстве биссектрисы угла получим, что точка O лежит
на биссектрисе угла ACB. Иначе говоря, биссектриса CC1
проходит через точку O. Таким образом, все три биссектрисы Теорема доказана. 2.Теорема о точке пересечения прямых, содержащих высоты треугольника. Ранее было введено понятие серединного перпендикуляра к отрезку и доказана теорема о серединном перпендикуляре: каждая точка серединного перпендикуляра к отрезку равноудалена от его концов. И обратно: если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.Воспользуемся этими свойствами для доказательства следующей теоремы. Теорема 3 (о точке пересечения серединных перпендикуляров к сторонам треугольника). Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Доказательство. Пусть
Докажем, что серединные перпендикуляры 1) Пусть O — точка пересечения
серединных перпендикуляров 2) Равенство OA = OC означает,
что точка O равно удалена от вершин A и C. Значит,
по теореме о серединном перпендикуляре точка O лежит на
серединном перпендикуляре к стороне AC. Таким образом, все три серединных перпендикуляра Теорема доказана. Воспользуемся теоремой 3 для доказательства свойства высот треугольника. Теорема 4 (о точке пересечения прямых, на которых лежат высоты треугольника). Прямые, на которых лежат высоты треугольника, пересекаются в одной точке. Доказательство. 1) Пусть отрезки
2) Проведем через вершины A, B и C прямые, параллельные сторонам BC, AC и AB соответственно. Пусть T, F и D — точки их пересечения. 3) Докажем, что точки A, B и C являются соответственно серединами сторон TD, TF и FD треугольника TFD. Например, докажем, что точка C — середина стороны DF. Так как четырехугольник ABCD — параллелограмм, то AB = DC. Так как ABFC — параллелограмм, то AB = CF. Таким образом, DC = CF. 4) Аналогично доказывается, что AT = AD и TB = BF. По условию AA1 ⊥ BC, а по построению TD ⃦ BC, следовательно,
Теорема доказана. Точка пересечения медиан, точка пересечения биссектрис и точка пересечения прямых, содержащих высоты треугольника, называются замечательными точками треугольника. Заметим, что если треугольник остроугольный, то пересекаются в одной точке сами его высоты, а если треугольник тупоугольный, то пересекаются в одной точке прямые, содержащие высоты.
|
|
VII. Этап усвоения новых знаний.
Цель этапа: поиск необходимой информации; самостоятельное планирование исследований, развитие умений делать выводы.
Педагогическая задача: способствовать формированию умений планировать свою деятельность, выделять нужную информацию, анализировать, обобщать.
|
Деятельность учителя |
Деятельность учащихся |
|
Решить: 1. Отрезок AT — биссектриса прямоугольного треугольника ABC с прямым углом при вершине C. Отрезок TK — перпендикуляр, проведенный к гипотенузе AB. Вычислите длину отрезка BK, если AC = 7см и AB =10 см. 2. Отрезок AO — биссектриса прямоугольного треугольника ABC с прямым углом при вершине C. Вычислите площадь треугольника AOB, если CO = 3 см, AB = 12 см.
3.Серединный перпендикуляр l к стороне AB параллелограмма ABCD пересекает сторону AD в точке F, которая является ее серединой (рис. 42, б).Вычислите расстояние от вершины B до точки F, если BC = 18 см.
4. Точки A и B лежат по одну сторону от прямой l.Постройте равнобедренный треугольник, основанием которого является отрезок AB, а вершина лежит на прямой l. |
Решают у доски и на месте. 1.
2.
3.
4.
|
VIII. Подведение итогов и рефлексия.
Цель этапа: осознание учащимися результативности своей деятельности на уроке, уровня усвоения учебного материала
Педагогическая задача: организовать условия для формулирования учащимися основ по учебной теме и оценивания своих собственных достижений.
|
Деятельность учителя |
Деятельность учащихся |
|
Предлагается вспомнить поставленные в начале урока цели и задачи и сделать вывод Учитель просит оценить свою работу в листе самооценки и ответить на вопросы: · какой способ работы над темой для тебя оказался самым продуктивным? -как вы считаете, какие из поставленных целей в начале урока нам удалось достичь? · определите одну из причин, которая не дала вам возможность повысить отметку · что надо сделать для улучшения результатов? |
Анализируют степень достижения поставленных целей, участвуют в подведении итогов урока. |
IX. Домашнее задание.
Педагогическая задача: подготовить учащихся к выполнению домашнего задания, предложить решить задание творческого характера.
|
Деятельность учителя |
Деятельность учащихся |
|
Домашнее задание : №90. |
Записывают домашнее задание. |
ОЦЕНКА РЕЗУЛЬТАТОВ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ ПО УЧЕБНОМУ ПРЕДМЕТУ «МАТЕМАТИКА»
Планируемые результаты обучения в предметно-деятельностной форме определены учебными программами в соответствии с требованиями Образовательного стандарта общего среднего образования учебного предмета “Математика” к уровню подготовки учащихся.
Поурочный контроль осуществляется в устной и письменной формах или в их сочетании посредством проведения опроса (индивидуального, группового, фронтального) с использованием контрольных вопросов и заданий, содержащихся в учебниках, учебных, учебно-методических пособиях и дидактических материалах, математических диктантов, собеседования, самостоятельных работ и других методов и средств контроля, которые определяются педагогом с учётом возрастных особенностей учащихся в целях получения объективной информации о качестве учебно-познавательной деятельности учащихся и их учебных достижениях.
Тематический контроль осуществляется посредством проведения самостоятельных и контрольных работ, других методов и средств контроля, которые определяются педагогом с учётом возрастных особенностей учащихся в целях получения объективной информации о качестве учебно-познавательной деятельности учащихся и их учебных достижениях.
Устанавливаются следующие показатели оценки результатов учебной деятельности учащихся при осуществлении контроля с использованием десятибалльной шкалы:
|
Баллы |
Показатели оценки
|
|
1 (один) |
Узнавание отдельных объектов изучения программного учебного материала, предъявленных в готовом виде (узнавание математических объектов, их свойств, признаков, математических формул, действий, правил, утверждений, моделей, составленных по условию задачи, других элементов математического знания, а также узнавание отдельных математических объектов в окружающей действительности)
|
|
2 (два) |
Различение объектов изучения программного учебного материала, предъявленных в готовом виде, и осуществление соответствующих практических действий (различение математических объектов, их свойств, признаков, математических формул, действий, правил, утверждений, моделей, составленных по условию задачи, других элементов математического знания и выделение заданных объектов изучения среди предъявленных и в окружающей действительности)
|
|
3 (три) |
Воспроизведение части программного учебного материала по памяти (описание математических объектов, перечисление их свойств и признаков; использование инструментов для измерения геометрических величин; выполнение заданий по образцу в одно-два действия)
|
|
4 (четыре) |
Воспроизведение большей части учебного материала по памяти (формулирование в устной или письменной форме свойств и признаков математических объектов, правил, утверждений, выделение при сравнении математических объектов общих и отличительных признаков без их объяснения; использование инструментов для проведения основных геометрических построений; выполнение заданий по образцу)
|
|
5 (пять) |
Осознанное воспроизведение значительной части программного учебного материала (описание математических объектов и связей между ними без их обоснования или доказательства, иллюстрация примерами окружающей действительности; решение типовых задач по заданному образцу)
|
|
6 (шесть) |
Осознанное воспроизведение в полном объёме программного учебного материала (описание математических объектов и связей между ними с элементами обоснования или доказательства; решение типовых задач по известному алгоритму, проверка результатов решения задач с использованием изученных методов)
|
|
7 (семь) |
Владение программным учебным материалом в знакомой ситуации (обоснование и доказательство математических утверждений при описании математических объектов с учётом внутрипредметных связей; решение типовых задач с использованием нескольких алгоритмов)
|
|
8 (восемь) |
Владение и оперирование программным учебным материалом в знакомой ситуации (развёрнутое описание математических объектов, раскрытие сущности математических понятий, правил, утверждений, доказательство математических утверждений, формулирование выводов, подтверждение примерами использования учебного материала в практической деятельности человека; самостоятельное решение типовых задач с полным их обоснованием)
|
|
9 (девять) |
Оперирование программным учебным материалом в частично изменённой ситуации (уверенное владение и оперирование учебным материалом для выполнения учебных заданий с использованием различных способов, приёмов, методов и учётом внутрипредметных и межпредметных связей)
|
|
10 (десять) |
Свободное оперирование программным учебным материалом, применение знаний и умений в незнакомой ситуации (владение приёмами математического моделирования; самостоятельные действия по описанию, объяснению и преобразованию математических объектов; нахождение рациональных способов решения задач, решение творческих задач) |
При оценке результатов учебной деятельности учащихся учитывается характер допущенных ошибок: существенных и несущественных.
К категории существенных относятся ошибки, свидетельствующие о том, что учащийся не знает формул, не усвоил математические понятия, правила, утверждения, не умеет оперировать ими и применять к выполнению заданий и решению задач.
К категории несущественных относятся отдельные ошибки вычислительного характера, погрешности в формулировке вопросов, определений, математических утверждений, небрежное выполнение записей, рисунков, графиков, схем, диаграмм, таблиц, а также грамматические ошибки в написании математических терминов.
Контрольная работа, самостоятельная работа, которые проводятся в рамках тематического контроля, должны включать по одному или по два задания в соответствии с показателями оценки результатов учебной деятельности учащихся при осуществлении контроля с использованием десятибалльной шкалы, установленными настоящими Нормами оценки результатов учебной деятельности.
Отметка за выполнение самостоятельных работ, которые проводятся в рамках тематического контроля, контрольных работ выставляется с применением следующих шкал: шкалы, определяющей максимальное количество баллов за каждое задание (шкалы 1, 3) и шкалы перевода суммарного количества баллов, полученных учащимся за выполнение соответствующей работы (шкалы 2, 4), в отметки по десятибалльной системе.
Шкала 1 Шкала 2
|
Шкала, определяющая максимальное количество баллов за каждое задание, если самостоятельная или контрольная работа содержит 5 заданий |
|
Шкала перевода суммарного количества баллов, полученных учащимся за выполнение самостоятельной или контрольной работы, которая содержит 5 заданий |
|
Номер задания |
Максимальное количество баллов за выполнение задания
|
|
1 |
2 |
|
2 |
4 |
|
3 |
6 |
|
4 |
8 |
|
5 |
10 |
|
|
Суммарный максимальный балл за выполнение всех заданий: 30 |
|
Количество баллов, полученных учащимся
|
Отметка по десятибалльной шкале оценки результатов учебной деятельности учащихся |
|
1 |
1 |
|
2 |
2 |
|
3—5 |
3 |
|
6—8 |
4 |
|
9—11 |
5 |
|
12—14 |
6 |
|
15—18 |
7 |
|
19—23 |
8 |
|
24—28 |
9 |
|
29—30 |
10 |
Шкала 3 Шкала 4
|
Шкала, определяющая макимальное количество баллов за каждое задание, если самостоятельная или контрольная работа содержит 10 заданий |
|
Шкала перевода суммарного количества баллов, полученных учащимся за выполнение самостоятельной или контрольной работы, которая содержит 10 заданий |
|
Количество баллов, полученных учащимся
|
Отметка по десятибалльной шкале оценки результатов учебной деятельности учащихся |
|
1 |
1 |
|
2—4 |
2 |
|
5—7 |
3 |
|
8—12 |
4 |
|
13—18 |
5 |
|
19—25 |
6 |
|
26—33 |
7 |
|
34—42 |
8 |
|
43—52 |
9 |
|
53—55 |
10 |
|
Номер задания |
Максимальное количество баллов за выполнение задания
|
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |
|
4 |
4 |
|
5 |
5 |
|
6 |
6 |
|
7 |
7 |
|
8 |
8 |
|
9 |
9 |
|
10 |
10 |
|
|
Суммарный максимальный балл за выполнение всех заданий: 55 |
Задание считается невыполненным, если в нём допущена существенная ошибка.
Количество баллов за выполнение задания снижается не менее чем на 10 процентов, если в нём допущена несущественная ошибка.
Структура и механизм оценивания самостоятельных работ, которые проводятся в рамках поурочного контроля, определяются педагогом в соответствии с показателями оценки результатов учебной деятельности учащихся при осуществлении контроля с использованием десятибалльной шкалы, установленными настоящими Нормами оценки результатов учебной деятельности.
Отметка за выполнение экзаменационных работ за период обучения на уровнях общего базового и общего среднего образования выставляется с применением шкал 2 и 4.
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
• касательная к окружности; секущая окружности; центральный угол; вписанный угол; описанная около треугольника окружность; вписанная в треугольник окружность; описанная около четырехугольника окружность; вписанная в четырехугольник окружность;
знать:
• свойство и признак касательной к окружности;
• свойство диаметра, перпендикулярного хорде;
• свойство угла, вписанного в окружность;
• свойство угла между пересекающимися хордами, между секущими, между касательной и хордой;
• свойство точки пересечения серединных перпендикуляров к сторонам треугольника;
• свойство точки пересечения биссектрис треугольника;
• свойство отрезков хорд, на которые они делятся точкой пересечения;
• свойство секущей и касательной к окружности, проведенных из одной точки;
• свойство и признак четырехугольника, описанного около окружности;
• свойство и признак четырехугольника, вписанного в окружность;
• формулы: радиуса окружности, описанной около прямоугольного треугольника; радиуса окружности, вписанной в прямоугольный треугольник;
уметь:
• применять при решении задач основные свойства и признаки геометрических фигур;
• применять теоремы при решении геометрических задач на доказательство и вычисление.
Планирование по теме «Вписанные и описанные многоугольники»
9 класс
(для учащихся, окончивших в 2017/2018 учебном году 9 классов 11-летней школы)
(2 ч в неделю, всего 29 ч)
|
9 Класс |
||
|
№ урока |
Тема урока |
Часы |
|
|
Вписанные и Описанные многоугольники |
29 |
|
1-4 |
Взаимное расположение прямой и окружности. Касательная к окружности |
4 |
|
5-9 |
Центральные и вписанные углы |
5 |
|
10-13 |
Замечательные точки треугольника |
4 |
|
14 |
Обобщение и систематизация знаний по теме «Касательная к окружности. Центральные и вписанные углы» |
1 |
|
15 |
Контрольная работа «Касательная к окружности. Центральные и вписанные углы» |
1 |
|
16 |
Коррекция знаний по теме «Касательная к окружности. Центральные и вписанные углы» |
1 |
|
17-21 |
Вписанные и описанные треугольники |
5 |
|
22-26 |
Вписанные и описанные четырехугольники |
5 |
|
27 |
Обобщение и систематизация знаний по теме «Вписанные и описанные многоугольники» |
1 |
|
28 |
Контрольная работа «Вписанные и описанные многоугольники» |
1 |
|
29 |
Коррекция знаний по теме «Вписанные и описанные многоугольники» |
1 |
В данной работе рассмотрена тема «Вписанные и описанные многоугольники»
В результате проведения работы были решены все поставленные задачи, и, тем самым, достигнута основная цель.
В данной работе мною были рассмотрены теоретические сведения, типовые задачи, задания для отработки умений и навыков, а так же самостоятельные и контрольные работы. В приложении 1 представлен план-конспект урока по теме «Вписанные и описанные многоугольники» и в приложении 2 план-конспект урока по теме «Замечательные точки треугольника». В приложении 3 Тема является одной из часто используемых в вычислениях и решении различных задач.
1. Учеб. пособие для 9-го кл. учреждений общ. А45 сред. образования с рус. яз. обучения / Е. П. Кузнецова [и др.] ; под ред. проф. Л. Б. Шнепермана. — 4-е изд., испр. и доп. — Минск : Народная асвета, 2014. — 287 с. : ил. ISBN 978-985-03-2201-2.
2. Геометрия : учеб. пособие для 9-го кл. учреждений общ. сред. образования с рус. яз. обучения / Е. П. Кузнецова [и др.] ; под ред. Л. Б. Шнепермана. — Минск : Нар. асвета, 2013.
3. Сборник задач по геометрии : учеб. пособие для 9 кл. учреждений общ. сред. образования с рус. яз. обучения / Е. П. Куз- нецова [и др.]. — Минск : Нац. ин-т образования, 2011.
4. Геометрия 9 : самост. и контр. работы : тестовые задания : в 4 вариантах : 1, 2 варианты : пособие для учителей учреж- дений общ. сред. образования с рус. яз. обучения / Е. П. Кузнецова [и др.]. — Минск : Аверсэв, 2014.
5. Геометрия 9 : самост. и контр. работы : тестовые задания : в 4 вариантах : 3, 4 варианты : пособие для учителей учреж- дений общ. сред. образования с рус. яз. обучения / Е. П. Кузнецова [и др.]. — Минск : Аверсэв, 2014.
6. Практикум по геометрии : пособие для учащихся 9-го кл. учреждений, обеспечивающих получение общ. сред. образования, с рус. яз. обучения / Е. П. Кузнецова [и др.]. — Минск : Аверсэв, 2005, 2008, 2010.
7. 11. геометрия 9 : самост. и контр. работы : тесты : пособие для учителей учреждений, обеспечивающих получение общ. сред. образования, с рус. яз. обучения / Е. П. Кузнецова [и др.]. — 5-е изд., перераб. — Минск : Аверсэв, 2014.
8. Сборник задач по геометрии : учеб. пособие для 9-го кл. учреждений, обеспечивающих получение общ. сред. образования, с рус. яз. обучения / Е. П. Кузнецова [и др.]. — Минск : Аверсэв, 2010
9. www adu.by
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.