ВВЕДЕНИЕ Процедура подготовки и решения задачи на ПК

ВВЕДЕНИЕ

Процедура подготовки и решения задачи на ПК – довольно сложный и трудоемкий процесс. В настоящее время на ПК решают самые разнообразные задачи, от расчета баллистических траекторий до завоевания инопланетных территорий (пока только в компьютерных играх). В каждом случае ПК выполняет какую-то программу. Некоторые из программ требуют от пользователя специальных знаний и высокой квалификации. Но, несмотря на бесконечное разнообразие программ, в самом процессе их создания можно увидеть нечто общее и выделить несколько этапов решения задачи на ПК.

Основные этапы процесса решения задачи на ПК:

-          математическая постановка задачи;

-          выбор метода решения задачи;

-          разработка алгоритма;

-          программирование;

-          отладка программы;

-          подготовка исходных данных и непосредственное выполнение программы.

Математическая постановка задачи

На этом этапе всем физическим величинам, участвующим в задаче, надо дать математические обозначения. Удобнее всего использовать общепринятые обозначения, например h - высота, l - длина, s - площадь и т.д., но допускается обозначать величины и произвольно, на свое усмотрение.

Следующее действие - определить так называемый "статус" каждой переменной, т.е. определить, к какой из следующих категорий она относится:

-          исходные данные - это величины, которые известны из условия задачи;

-          результат - это величины, которые требуется найти;

-          промежуточные данные - это величины, которые не известны заранее, но определяются в ходе решения задачи для того, чтобы найти результат.

Выбор метода решения задачи

Как правило, для большинства задач методы решения уже разработаны, и нередко в нескольких вариантах. Остается только выбрать тот, который больше всего отвечает некоторым требованиям

5

(минимальный объем памяти, минимальная трудоемкость, максимальная эффективность, достаточная точность, допустимая погрешность вычислений и т.д.). В математике, например, известны методы точных вычислений и методы приближенных вычислений (для поиска корней нелинейных уравнений, вычисления определенных интегралов и т.п.).

Часто для реализации одного и того же численного метода можно предложить несколько алгоритмов, различающихся по своей простоте, объему вычислительной работы, емкостным затратам и т.д. Для решения задачи стараются выбрать алгоритм, обеспечивающий наиболее эффективное использование машины.

Разработка алгоритма

Само слово “алгоритм” происходит от имени персидского математика Аль Хорезми, который в IX веке разработал правила четырех арифметических действий.

Алгоритм - это описание некоторой последовательности арифметических и логических действий над числовыми значениями, которые приводят к получению результата решения задачи при различных исходных данных.

Этот этап, пожалуй, самый важный. Разработка алгоритма является сложным и трудоемким процессом. На данном этапе создается подробный план решения задачи. Успешная разработка алгоритма позволяет избежать многих ошибок, поскольку именно на этом этапе определяется логика будущей программы. А ведь труднее всего находить и исправлять логические ошибки.

Если к разработке алгоритма отнестись недостаточно внимательно, то в дальнейшем, на этапе программирования появятся трудности, алгоритм потребует дополнительной доработки. Также может выясниться, что, к сожалению, алгоритм дает ошибки или вообще не выполним, и нужно разработать другой.

Алгоритм - это не просто последовательность действий, а обладающая определенными свойствами (характеристиками). К основным свойствам алгоритма относятся:

-         массовость: алгоритм позволяет получить результат при различных исходных данных;

-         результативность: алгоритм должен приводить к получению результата за конечное число шагов, т.е. быть обязательно конечным;

6

-         определенность: предписания, входящие в алгоритм, должны быть точными и понятными исполнителю, однозначными и не оставлять места для ее неоднозначного толкования и неопределенного исполнения;

-         дискретность: алгоритм может быть разбит на отдельные элементарные шаги, возможность выполнения которых на компьютере интерпретируется однозначно.

Наиболее простой и универсальной формой представления алгоритма является словесное описание, которое содержит записанную на естественном языке, точнее, на языке предписаний, четкую пошаговую последовательность предписаний.

Но наглядностью обладает форма записи алгоритма в виде графической схемы. Графический способ описания алгоритма (блок- схема) получил самое широкое распространение. Для графического описания алгоритмов используются блоки, которые соединяются между собой линиями связи (см. приложение 1).

Каждый этап вычислительного процесса представляется геометрическими фигурами, т.е. блоками. Они делятся на арифметические или вычислительные (прямоугольник), логические (ромб) и блоки ввода-вывода данных (параллелограмм). Внутри блока дается описание соответствующего действия (см. рис.1).

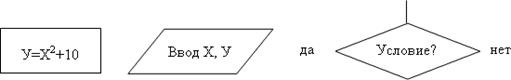Рис. 1 - Изображение этапов вычислительного процесса Порядок выполнения этапов указывается стрелками,

соединяющими блоки. Геометрические фигуры размещаются сверху вниз и слева на право. Нумерация блоков производится в порядке их размещения в схеме. Недостатком графических схем алгоритмов является громоздкость.

Программирование

Это процесс записи алгоритма на одном из алгоритмических языков программирования. Таких языков существует немало. Наиболее распространены Бейсик, Паскаль, СИ и др.

Следует отметить, что этап программирования не будет представлять большой сложности, если алгоритм разработан

7

достаточно тщательно. Чем больше внимания уделяется разработке алгоритма, тем меньше времени придется затратить на написание программы, которое в этом случае будет выглядеть как простой перевод. Качественно разработанный алгоритм сможет программировать человек, владеющий языком программирования, но совершенно не знакомый, ни с постановкой задачи, ни с методом ее решения.

Программа должна быть наглядной, легко читаться, сопровождаться комментариями. В комментариях рекомендуется указывать назначение отдельных участков программы, смысл используемых переменных, пояснение наиболее сложных участков.

Отладка программы

Это процесс поиска (диагностики) и устранения ошибок в программе путем решения ее на контрольных (тестовых) примерах. Надо подобрать разные наборы исходных данных, чтобы проверить правильность работы программы при всех возможных исходах.

Главное правило подбора тестовых примеров состоит в следующем: тесты следует подбирать таким образом, чтобы они не подтверждали правильность программы, а выявляли имеющиеся в ней ошибки.

Ошибки в программе бывают двух видов:

-          ошибки ввода (описки) и синтаксические ошибки записи операторов - выявляются при трансляции программы на машинный язык. Программа-транслятор выводит на экран компьютера сообщение о характере ошибки и указывает место в программе, где эта ошибка была обнаружена.

-          смысловые (алгоритмические) ошибки - выявляются на этапе отладки работающей программы, когда программа не производит в точности ожидаемых действий, сообщений об ошибках при этом нет. Обнаруживаются такие ошибки только при сравнении результатов машинного и ручного просчета.

При отладке большой сложной программы используются следующие методы:

-          распечатка значений промежуточных данных, помогает найти ошибки в вычислениях;

-          трассировка программы (trace - след) - вывод номеров операторов по мере их фактического выполнения, дает возможность проследить последовательность выполнения отдельных действий и частей программы;

8

-          пошаговое выполнение с просмотром содержимого памяти, выполняется с помощью специальной программы - диалогового отладчика.

Подготовка исходных данных и непосредственное выполнение программы

Исходные данные, если они объемные, могут быть подготовлены отдельно, на внешнем носителе (на жестком диске или дискете) или же введены с клавиатуры.

Если все предыдущие этапы завершились благополучно, то выполнение программы происходит почти автоматически, не требует особых затрат и может быть проведено человеком, не принимавшим участия в предварительной работе над задачей.

Рассмотрим последовательность прохождения этапов на примере решения простой задачи.

На первом этапе формулируется условие задачи, например, в словесной форме: функция f(x) должна получить значение, равное единице, если переменная x больше нуля, и ноль, если переменная x принимает другие значения.

Для уяснения задачи можно представить ее в графическом виде: на числовой оси отложить точку 0 и отметить значения переменной x, при которых функция f(x) принимает 0 или 1 (см. рис. 2).

Рис. 2 - Графическая интерпретация условия задачи

На втором этапе производится математическая постановка задачи (математическая модель):

-          определяются исходные (вводимые) данные и их типы. В данной задаче к исходным данным относится переменная x, которая может принимать целые и вещественные значения. В качестве типа для переменной x выбирается вещественный, поскольку данный тип включает в себя и целые значения тоже;

-         

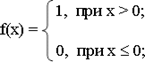9

-          определяются конечные (выводимые) данные и их типы. В данной задаче конечными данными (результатом решения) является значение функции f(x) целого типа.

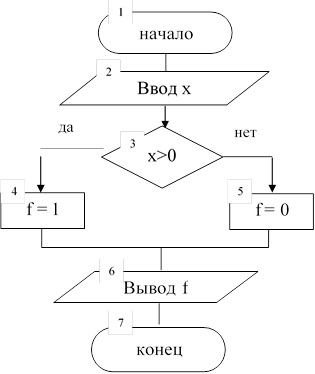
На третьем   этапе   осуществляется   разработка   алгоритма.

Алгоритм решения задачи показан на рис. 3.

На четвертом этапе решения задачи алгоритм переводится в программу, записанную на алгоритмическом языке. На рис.3 приводятся программы на языках программирования Turbo Pascal и QBasic, которые реализуют данный алгоритм.

Pascal

Program zadacha;

Var x:real; f:integer;

Begin

End.

Read (x);

If     x>0 Then f:=1

Else f:=0; Writeln („f=‟, f);

QBasic

REM zadacha

DEFSNG X : DEFINT F INPUT X

IF X>0 THEN F=1 ELSE F=0 PRINT “F=”; F

END

Рис. 3 - Алгоритм и программа решения задачи

На пятом этапе программа вводится в память компьютера, осуществляется ее отладка и решение.

Больше всего времени, как правило, требуется на выполнение этапа отладки и решения. Это связано с тем, что здесь устраняются ошибки, допущенные пользователем на всех предыдущих этапах решения задачи. Если это ошибки синтаксиса или семантики, они достаточно легко устранимы. Хуже наличие алгоритмических ошибок, выявить которые значительно труднее, а для их устранения требуется осуществлять многократное тестирование программы для различных наборов исходных данных.

Скачано с www.znanio.ru