Выражения с переменными

Выражения с переменными

Цели: продолжить формировать умение находить значение выражения с переменными; формировать умение составлять выражение с переменными  по  условию  задачи,  в  том  числе  формулы,  и  находить  их значение.

Ход урока

I. Устная работа.

1.  Найдите значение выражения 3а – b, если:

а) а = 2 и b = –4;              б) а = 0 и b = ;

в) а = –4 и b = 5;              г) а = – и b = .

3. Сколько процентов составляет:

а) 50 от 200;                     б) 13 от 260;

в) 1,5 от 20;                     г) 240 от 80?

Проверочная работа

Вариант 1

1. Заполните таблицу: 

2. Найдите значение выражения х + у – 2z, если х + у = 3 и z = –2.

Вариант 2

1. Заполните таблицу:

2. Найдите значение выражения а – b + 3c, если а – b = 11 и с = –6.

II. Объяснение нового материала.

Вводится понятие формулы. Приведу примеры различных формул, применяемых на практике (вычисление площадей, объемов, числовые формулы и т. п.). Также следует объясняю, что есть стабильные формулы, которые уже выведены и могут использоваться для расчетов. А есть задачи, для решения которых необходимо самостоятельно выявить закономерности (зависимости), описанные в условии, ввести переменные, составить выражение с переменными (формулу) и использовать его для вычисления искомого задачи при конкретных исходных данных.

III. Формирование умений и навыков.

1.      № 29.

Решение:

Если площадь первого участка, а га, а с каждого га собрали 32 ц пшеницы, то со всего участка собрали 32а ц пшеницы. Аналогично получаем для второго участка урожай 40b ц пшеницы.  Тогда с обоих участков был собран урожай 32а + 40b (ц).  Если а = 120 и b = 80, то 32а + + 40b = 32 · 120 + 40 · 80 = 3840 + 3200 = 7040.

Ответ: 32а + 40b (ц); 7040 ц.

2.      № 31.

Решение:

Фигура состоит из отдельных частей. её площадь можно найти двумя способами:

1-й способ.

«Разбить» фигуру на отдельные фигуры, для которых можно легко найти площадь, и, сложив полученные результаты, получить общую площадь.

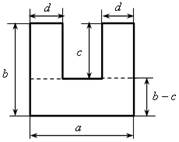
Площадь состоит из суммы площадей трех прямоугольников со сторонами: d и с; d и с; а и b – с.  Их площади соответственно равны: сd; сd; а (b – с). Значит, площадь искомой фигуры составляет:

сd + сd + а (b – с) или    2сd + а (b – с).

2-й способ.

Представить фигуру в виде прямоугольника со сторонами а и b с «вырезанным» прямоугольником со сторонами с и а – 2d. Их площади соответственно равны аb и с (а – 2d). Значит, площадь искомой фигуры составляет аb – с (а – 2d).

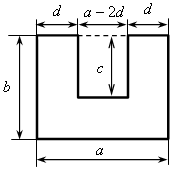
Ответ: 2сd + а (b – с) (см²) или аb – с (а – 2d) (см²).

3. № 33.

Решение:

После добавления   5 г  соли  в  раствор  масса   его  стала  равна 255 г. Масса  чистой  соли  в  растворе  также  увеличилась  на  5 г  и  стала  составлять  (х + 5) г.  Концентрация   соли,   таким   образом,  составляет  ∙  100 %.

Ответ:  ∙  100 %.

1. № 37 (устно); № 38.

2. № 39 (устно); № 40 (устно).

3. № 41 (устно); № 42.

4. № 35 (устно); № 36 (устно).

iV.  Итоги урока.

– Что называется значением выражения с переменными?

– В каком случае выражение с переменными не имеет смысла? Назовите выражение, которое содержит переменную х и которое не имеет смысла при х = –3,5.

– Назовите выражение, имеющее смысл при любых значениях входящей в него переменной у.

– Что представляет собой формула? Назовите формулу четного числа, нечетного числа.

Домашнее задание: 1. № 30, № 32,