Выступление на МО

Тема: Подходы к решению задач по программе                           «Школа России»

Свое выступление я начну с пояснения « что же такое решение задач?»

термин «решение задачи» широко применяется в математике. Этим термином обозначают связанные между собой, все же неодинаковые понятия:

ü решением задачи называют результат, т.е. ответ на требование задачи;

ü решением задачи называют процесс нахождения этого результата, т.е вся деятельность человека, решающего задачу, с момента начала чтения задачи до конца;

ü решением задачи называют  лишь те действия, которые происходят над условиями и их  следствиями на основе общих положений математики для получения ответа задачи.

Анализируя  учебники математика прошлых лет и учебники по новым ФГОС по программе «Школа России», наша группа нашла следующие изменения.

-обновлена тематика задач,

-введен разнообразный геометрический материал,

-даны занимательные задания, развивающие логическое мышление и воображение детей.

Если раньше мы учились решать задачи, то в рамках ФГОС:

-открытие новых знаний в процессе в процессе собственной деятельности, т.е. «обучение, обеспечивающее включения детей в учебно – познавательную деятельность»

-использование личного жизненного опыта, жизненных ситуаций.

По программе «Школа России»определены следующие подходы к решению задач:

ü частный подход – знакомство с алгоритмом и доведен е его до автоматизма;

ü общий подход – заключается в знании, что такое задача, знании этапов решения задачи и умении выполнять эти этапы.

Частный подход основан на видах и типах задач, а общий на 4 этапах решения любой задачи.

4 этапа:

1.    Анализ содержания задачи.

2.    Поиск плана решения.

3.    Выполнение плана решения задачи.

4.    Проверка.

Задачи, используемые по программе «Школа России»

-задачи с неполными данными,

-моделирование задач по схеме, краткой записи, по таблице, по диаграмме, по чертежу,

-составление задач, связанных с жизненными ситуациями,

-соотнесение решений с разными решениями,

-постановка вопроса к условию,

-решение задач разными способами,

- решение задач с лишними данными,

-составление и решение задач с использованием формул,

-логические и нестандартные задачи.

В программе «Школа России» рекомендованы методы для решения задач:

·       арифметический,

·       алгебраический,

·       графический,

·       практический,

·       логический,

·       смешанный,

·       табличный,

·       с помощью диаграмм.

Учителя, работая по программе «Школа России», используют 2 вида разбора сложной задач:

Ø синтетический (рассуждения ведем от данных задач к ее вопросу),

Ø аналитический (от вопроса задачи – к данным)

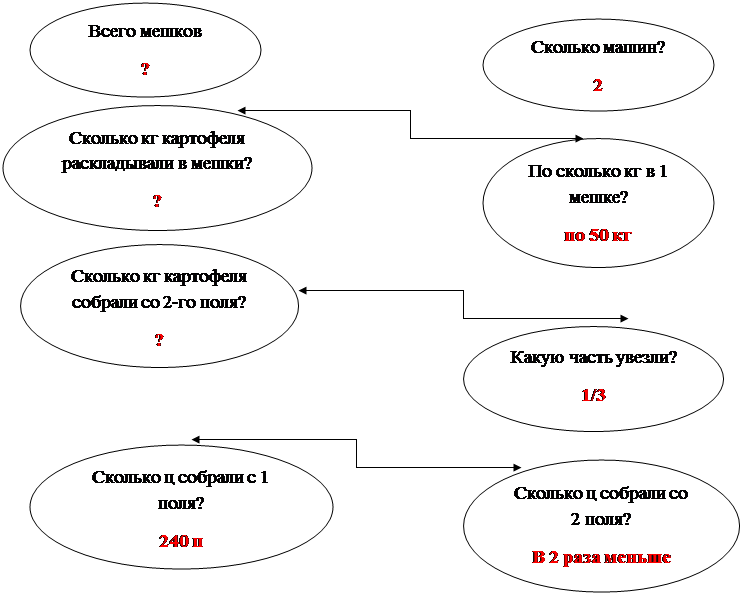
При аналитическом способе решения задачи выясняется, что нужно предварительно узнать, чтобы ответить на вопрос задачи. Чтобы помочь детям вести рассуждения аналитическим способом, можно использовать прием, называемый «деревом рассуждений». Суть его  состоит в том, что по ходу рассуждений строится схема, которая помогает увить, какие простые задачи следует выделить и каким будет план решения данной составной задачи.

Рассмотрим задачу из учебника «Математики» в 4 классе по программе «Школа России»

ü С одного поля собрали 240 ц картофеля, с другого в 2 раза меньше. 3-ю часть картофеля, собранного со 2-го поля, разложили в мешки по 50 кг каждый и увезли с поля поровну на 2-х машинах. Сколько мешков положили на каждую машину?

Составим модель задачи:

Собрали: 1п.-240ц

2п.-?ц, в 2 раза<

Разложили: 1/3 со 2 п. пго 50 кг-? м.

увезли на 2-х машин по ? М.

 А теперь составим схему рассуждения по аналитическому способу.

		Сколько мешков                                   на 1 машине?

Теперь вспомним синтетический способ решения задач.

Он характеризуется тем, что основным вопросом при поиске решения задачи является вопрос   том, что можно найти по двум или нескольким известным в тексте задачи числовым значениям. По вновь полученным числовым значениям. По вновь полученным числовым значениям и другим из