Y = arcsin x ֆունկցիայի հատկություններն ու գրաֆիկը

y = arcsin x ֆունկցիայի հատկություններն ու գրաֆիկը

    x թվի արկսինուս կոչվում է [−π/2;π/2] հատվածի այն թիվը, որի սինուսը x-ն է: 

    Հիշենք, որ y=sinx ֆունկցիան [−π/2;π/2] հատվածում խիստ աճում է, հետևաբար հակադարձելի է:

     Յուրաքանչյուր x∈[−1;1] թվին համապատասխանեցնելով y=arcsinx թիվը՝ ստանում ենք [−1;1] հատվածում որոշված ֆունկցիա՝ y=arcsinx, −1≤x≤1:

     y=arcsinx-ը y=sinx-ի հակադարձ ֆունկցիան է, որտեղ −π2≤x≤π/2

    Հետևաբար,

 ա) կամայական x∈[−1;1] թվի համար sin(arcsinx)=x,

բ) կամայական –π/2≤x≤π/2 թվի համար arcsin(sinx)=x:

     y=sinx-ի հատկությունների միջոցով կարելի է ստանալ նրա հակադարձ ֆունկցիայի՝ y=arcsinx-ի հատկությունները: 

    Մասնավորապես, y=arcsinx-ի, որտեղ –π/2≤x≤π/2, գրաֆիկը համաչափ է y=sinx-ի գրաֆիկին՝ y=x առանցքի նկատմամբ:  

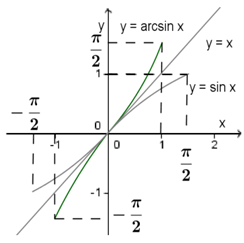
    y=arcsinx ֆունկցիայի հատկությունները.

   1. y=arcsinx ֆունկցիայի որոշման տիրույթը [−1;1] հատվածն է:

   2. y=arcsinx ֆունկցիայի արժեքների բազմությունը [−π/2;π/2] հատվածն է: 

   3. y=arcsinx-ը աճող ֆունկցիա է: 

   4. y=arcsinx ֆունկցիան կենտ է՝ arcsin(−x)=−arcsinx: