УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
Язык программирования ![]()
к.ф.-м.н., доцент
Мусин Наиль Минбариевич
Новомосковск 2015
СОДЕРЖАНИЕ
Mind Map. 3
Введение. 4
Начало работы.. 5
Установка рабочей папки. 5
CTRL+L.. 6
Числа и переменные. Функция c() 9
Округление. 9
Функции пользователя. 11
Векторы, их сложение и вычитание. Скалярное произведение. 12
Отбор элементов вектора. Сортировка. 12
Матрицы.. 13
Сложение. Умножение. 14
Действия над строками и столбцами. 16
Определитель. 17
Обратная матрица. 17
СЛАУ.. 18
Списки. Функция list() 20
Таблицы (фреймы). Функция frame() 20
Работа с файлами. 20
Блокнот. 21
Excel 23
Программирование. 25
for, while, векторизация. 25
if. 26
switch. 26
r-файлы.. 26
Эконометрика. 27
Однопараметрическая регрессия. 27
Множественная регрессия. 35
Временны́е ряды.. 40
Заключение. 45
Использованные источники. 46
Mind Map
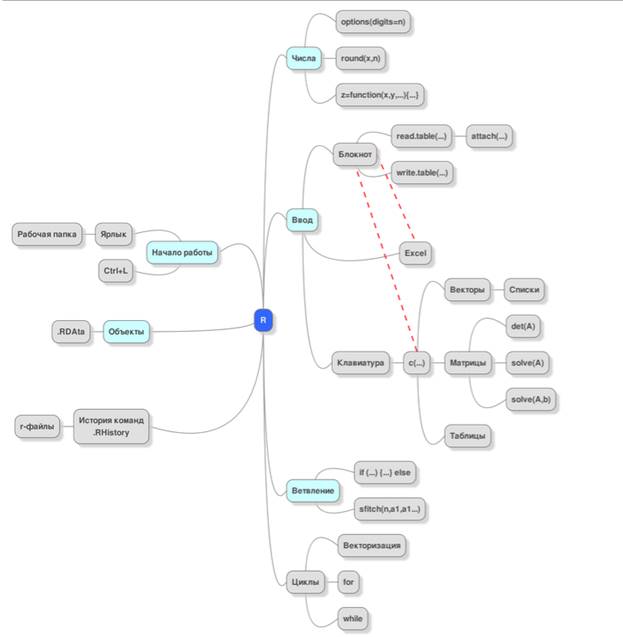
Введение
В пособии даётся представление об одном из самых мощных, профессиональных и современных средств работы с числами, начиная от простых вычислительных задач и заканчивая статистической обработкой больших массивов данных – языке R. Несмотря на это, он может быть установлен даже на USB-флеш диск.
Объектно-ориентированный язык R является свободно распространяемым и бесплатным, имеет интерфейс командной строки. Создан в 2011 году программистами Ross Ihaka и Robert Gentleman (Новая Зеландия, Оклендский университет). R является свободной реализацией языка S, который был разработан в компании Bell Laboratories Риком Бекером, Джоном Чамбером и Алланом Вилксом и который лежит в основе коммерческой программы S-Plus.
Первоначально язык R (как и язык S) создавался для статистических расчётов, но с тех пор его возможности вышли далеко за пределы статистики. Однако, для сравнения, укажем, что в статистических расчётах он намного превосходит возможности таких оконно-кнопочных неспециализированных программ, как MS Excel, Gnumeric, OpenOffice.org Calc, и специализированных программ STATISTICA, STADIA, PAST, SPSS, MiniTab, StatGraphics, а также с интерфейсом командной строки SAS, Stata, SYSTAT, S-Plus.
В частности, знакомство с языком R навсегда отбивает у российского пользователя считать что-либо в Excel.
Кроме того, польза от овладения R состоит в том, что можно научиться ценить чистый командный интерфейс, запуская x64\R.exe или i386\ R.exe. Минимальный графический интерфейс запускается x64\Rgui.exe или i386\Rgui.exe. Командный интерфейс среды R настолько прост и понятен, что необходимость в графических интерфейсах напрочь отпадает. Некоторые недостатки работы с командной строкой можно обойти, готовя программу в текстовом редакторе Блокнот.
Начало работы
Скачать
последнюю версию можно по адресу
https://cran.r-project.org - выбрать Download R for Windows, выбрать base,
нажать затем на Download R 3.5.1 for Windows
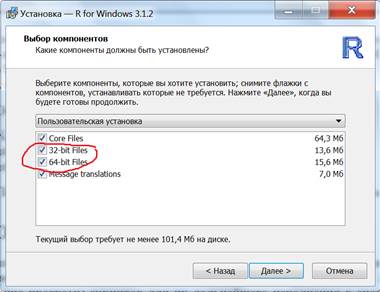
При выборе файлов (из двух обведённых на рисунке) нужно предварительно выяснить разрядность компьютера. Можно выбрать оба файла.
В данной работе рекомендуется запускать x64\Rgui.exe или i386\Rgui.exe с минимальным графическим интерфейсом и не рекомендуется устанавливать более «продвинутые» графические оболочки, которые в среде R, как показывает опыт, лишь намного усложняют, а не упрощают работу. В среде R намного проще, быстрее и логичнее добиться результата с помощью командной строки.
Установка рабочей папки
Обязательно
нужно установить ярлык программы на рабочий стол.
Затем на каком-либо логическом диске создать папку (например,
D:\R_Directory), щелкнуть по ярлыку правой кнопкой мыши и в поле
Рабочая папка
вписать путь к созданной папке:
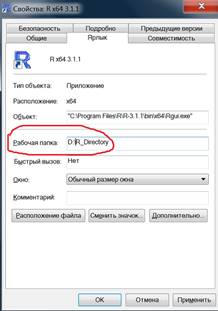
Все создаваемые файлы будут автоматически сохраняться в этой рабочей папке, и в этой же папке будут создаваться с помощью текстового редактора Блокнот файлы с числовыми данными для последующей обработки в среде R.
CTRL+L
В самом начале работы в R каждый раз появляется и каждый раз надоедает уже наполовину заполненное рабочее окно:
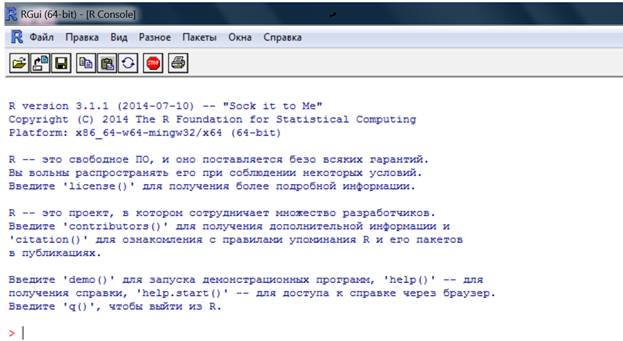
Раз и навсегда избавиться от этого «приветствия» невозможно.
Чтобы очистить экран, осваиваем первую команду CTRL + L . Она будет применяться и в дальнейшем по мере заполнения экрана.
Но эта команда ничего не уничтожает, она как бы прокручивает экран вверх. Всё, что делается, накапливается в виде электронного «свитка», и при закрытии программа задаёт стандартный вопрос:
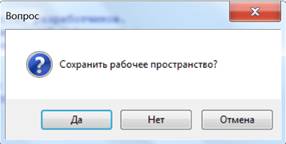
При согласии всё наработанное будет сохранено в двух файлах:
1) .Rhistory – здесь все введённые в ходе работы команды, и
2) .Rdata – здесь все созданные в ходе работы объекты.
Эти файлы можно найти в вышеописанной рабочей папке и, при необходимости, можно отредактировать файл .Rhistory в текстовом редакторе Блокнот .
Если же отказаться сохранить рабочее пространство, то всё наработанное исчезнет, и при следующем запуске всё начнётся «с чистого листа».
Чтобы быть уверенными в том, что новый проект начнётся с «чистого листа», можно вообще удалить файлы .Rhistory и .Rdata. Среда R создаст новые, «чистые» копии этих файлов.
Иногда советуют, что, если нужно начать «с чистого листа», не закрывая программу, то нужно набрать команду rm(list=ls()), или через меню: Разное à Удалить все объекты . Однако при этом история команд сохраняется. Поэтому лучше всё-таки закрыть программу, удалить файлы .Rhistory и .RData и затем запустить программу.
Числа и переменные. Функция c()
Как работать с числами и переменными, ясно из следующего рисунка:
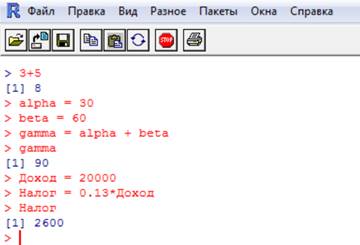
Знак равенства означает присваивание, а в конце команды точка с запятой не ставится.
Две распространённые константы:
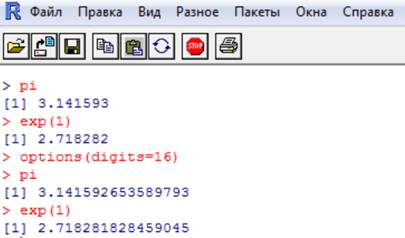
Округление
Количество n десятичных знаков дробной части для округляемого числа x устанавливается с помощью команды round(x, n):
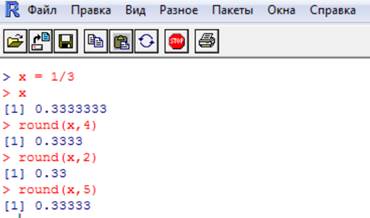
Но если надо получить больше десятичных знаков, то сейчас ничего не получится. Надо сначала с помощью команды digits установить максимально возможное в R количество десятичных знаков, равное 16, причём последующие цифры уже неверны:
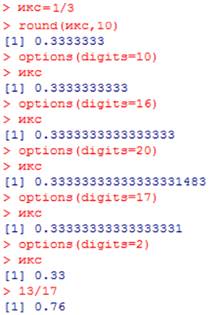
Если установить команду digits(икс, n), то все дальнейшие результаты будут с n знаками после запятой.
Очень важным является то, что каждая переменная является на самом деле именем массива, то есть вектора. Даже если вводится только одно число, для него заводится массив из одной ячейки:
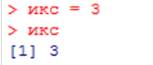
Число 1 в квадратных скобках показывает, что в 1-й ( и единственной) ячейке массива записано число 3.
Далее с этой переменной можно производить любые действия. Например:

Если же надо ввести
одномерный массив (вектор), то используется функция ![]() создания одномерного массива
однотипных элементов
создания одномерного массива
однотипных элементов ![]() . Функция
применяется к вектору покомпонентно:
. Функция
применяется к вектору покомпонентно:
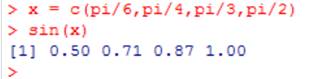
Очень важным является то, что переменные можно называть не только латинскими буквами, но и русскими. Это упрощает восприятие пользователями программных продуктов, связанных, например, с учётом товаров на складе, или с бухгалтерским учётом. И вообще восприятие русскоязычным пользователем и программистом переменных на русском языке желательнее.
Функции пользователя
Пример таких функций: ![]()

Векторы, их сложение и вычитание. Скалярное произведение

Отбор элементов вектора. Сортировка
Пример: пусть в вектор занесены возрасты сотрудников по мере их поступления на работу. Требуется сделать выборку сотрудников возраста от 30 до 35 лет:

Очевидно, что можно формировать сложные запросы с помощью логических операторов:
|
"Равно" == |
"Больше либо равно" >= |
|
"Не равно" != |
"Логическое И" & |
|
"Меньше" < |
"Логическое ИЛИ" | |
|
"Больше" > |
"Логическое НЕ" ! |
|
"Меньше либо равно" <= |
|
Сортировать элементы вектора можно следующим образом:

Матрицы
Матрицы создаются из векторов следующим образом:

Как видим, элементы вектора выписываются сверху вниз по столбцам. Чтобы элементы выписывались слева направо по строкам, следует это указать следующим образом:



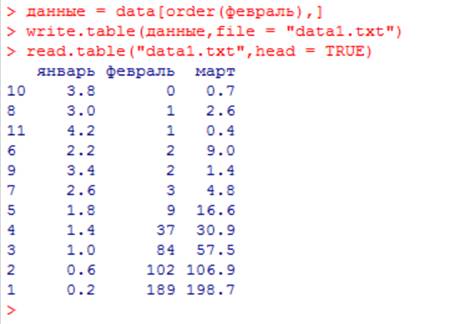
Отсортированную матрицу можно сохранить на жёсткий диск:
Сложение. Умножение
![]()





Действия над строками и столбцами

Соединяем вместе строки и столбцы матриц М и В в одну матрицу:

Определитель


Обратная матрица
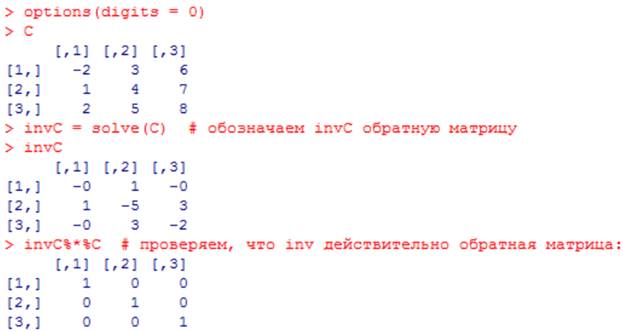

СЛАУ
Не знающий, что такое СЛАУ – да не читает этот пункт.
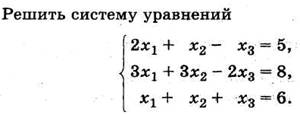

Проверим полученное решение:

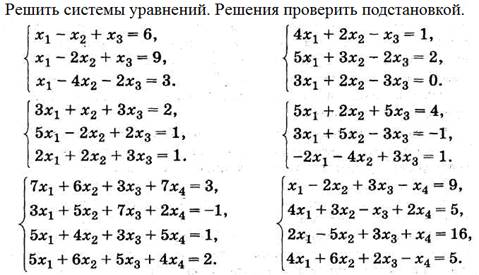
Списки. Функция list()
Векторы можно объединить в так называемые списки с помощью функции list(), при этом векторы могут быть разных типов и разной длины.

Таблицы (фреймы). Функция frame()
Таблица в R аналогична таблицам программы Excel и ей подобных табличных процессоров: столбцы, то есть векторы, могут состоять из ячеек различных форматов (типов), но должны состоять из одинакового количества элементов. Таблица в R – частный случай списка.

Работа с файлами
До сих пор данные в R вводились с клавиатуры. Однако данные можно набирать сначала в текстовом редакторе Блокнот , а потом считывать данные из соответствующего файла. Эта возможность есть во всех языках программирования, но в R этот процесс реализован намного проще, красивее и изящнее - скорее всего потому, что язык R работает на текстовом коде, и нет здесь никаких fopen, fclose.
Блокнот
Допустим, наши данные располагаются в трёх столбцах x, y и z.
Заходим в рабочую папку среды R и в Блокноте набираем через пробел имена столбцов, например, январь, февраль, март. Они составляют заголовок (head).
Во второй и последующих строках набираем данные, отделяя их пробелом. Пусть получилось следующее:
январь февраль март
0.2 189 198.7
0.6 102 106.9
1.0 84 57.5
1.4 37 30.9
1.8 9 16.6
2.2 2 9.0
2.6 3 4.8
3.0 1 2.6
3.4 2 1.4
3.8 0 0.7
Сохраним данные в файле data.txt.
Запускаем среду R и в рабочем окне набираем команду
данные = read.table(“data.txt”, head = TRUE) :
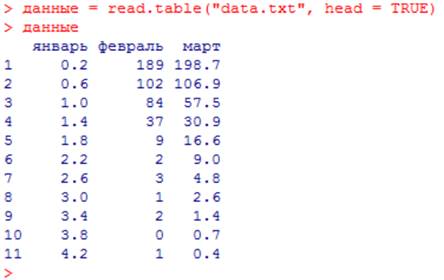
Как видим, заголовок надо включать опцией head = TRUE.
Для того, чтобы со столбцами можно было обращаться как с отдельными объектами, следует их имена включить в пространство имён командой attach(данные). Тогда можно будет, например, покомпонентно сложить все три столбца:

Мы также можем просуммировать числа отдельно по столбцам, а можно и все числа в таблице:

Можно подсчитать средние значения:

Excel
Часто данные бывают сохранены в формате Excel. Например:
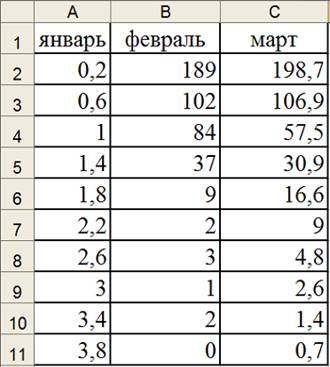
Следует сохранить его в формате .txt, но таких форматов Excel предлагает несколько. Следует выбрать Текст Юникод (*.txt) и сохранить, например, в файл по имени data.txt:
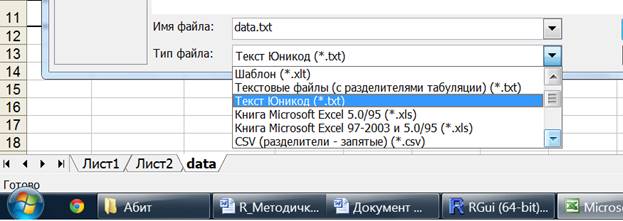
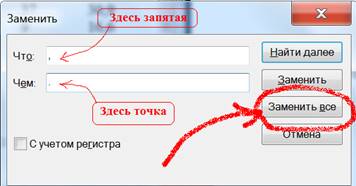
Открыв в Блокноте файл data.txt, видим:
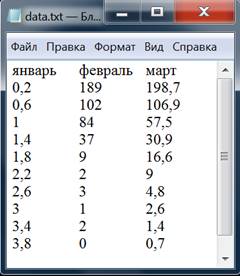
В Excel употребляется десятичная ЗАПЯТАЯ, в то время как в R употребляется десятичная ТОЧКА, поэтому следует произвести соответствующую замену:
|
|
|
Полученный файл data.txt следует переместить в рабочую папку среды R.
Программирование
for, while, векторизация
Про циклы for, while далее не будет ни слова (справку можно легко получить в среде R), ибо без них в R можно вообще обойтись за счёт так называемой векторизации вычислений. Это означает, что можно выполнить некоторые операции сразу над всеми элементами вектора, матрицы:

Более сложный пример:

На практике этого бывает достаточно.
Вот типичный пример решения задач с применением for:
Задача.
Вычислить ![]()
Вот решение в Паскале:
Var S, X, Pr : Real; N, I : Integer;
Begin
Write('Введите число слагаемых и x: '); ReadLn(N, X);
Pr := 1;
S := 0;
For I := 1 To N Do
Begin
Pr := Pr * Sin(X);
S := S + Pr
End;
WriteLn('Сумма равна ', S : 7 : 4)
End.
А вот решение в R:
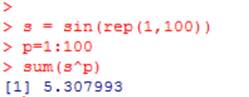
if

switch

r-файлы
Последовательность совершенных действий можно сохранить в текстовый файл:
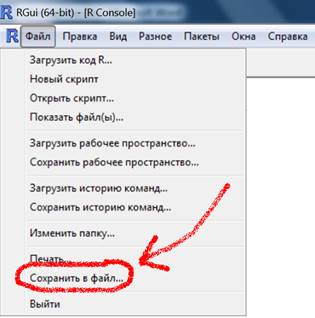
расширение txt заменить на r (пусть файл назвали xxx.r), открыть файл в Блокноте и отредактировать, в частности, убрать значок ввода >
Чтобы запустить этот файл, нужно ввести команду source(“xxx.r”)
Эконометрика
Однопараметрическая регрессия
Проведём анализ связи между кредитами, предоставленными предприятиям, организациям, банкам и физическим лицам, млн руб., и основными фондами в экономике (по полной балансовой (учетной) стоимости; на конец 2001 года, по следующим данным:
Социально-экономические показатели субъектов РФ на начало 2001 г.
|
Регион |
Кредиты, предоставленные предприятиям, организациям, банкам и физическим лицам, млн руб. |
Основные фонды в экономике (по полной балансовой (учетной) стоимости; на конец года), млн руб. |
|
Белгородская область |
342,5 |
145787 |
|
Брянская область |
275,4 |
113415 |
|
Владимирская область |
112,1 |
129272 |
|
Воронежская область |
274,5 |
211898 |
|
Ивановская область |
141,5 |
84550 |
|
Калужская область |
129 |
105783 |
|
Костромская область |
50,7 |
83716 |
|
Курская область |
401,3 |
124453 |
|
Липецкая область |
125,3 |
129114 |
|
Московская область |
5814,2 |
659675 |
|
Орловская область |
58 |
64366 |
|
Рязанская область |
456,5 |
110379 |
|
Смоленская область |
192,2 |
125247 |
|
Тамбовская область |
82,3 |
111642 |
|
Тверская область |
319,1 |
175833 |
|
Тульская область |
638,3 |
156543 |
|
Ярославская область |
727,9 |
185442 |
|
Москва |
811856,3 |
1384509 |
|
Республика Карелия |
41 |
90800 |
|
Республика Коми |
654,1 |
201201 |
|
Архангельская область |
103,3 |
198340 |
|
Вологодская область |
2411,2 |
136362 |
|
Калининградская область |
784,4 |
75707 |
|
Ленинградская область |
244,7 |
223013 |
|
Мурманская область |
490,7 |
144824 |
|
Новгородская область |
221,8 |
65864 |
|
Псковская область |
163,5 |
74695 |
|
Санкт–Петербург |
41581 |
412221 |
|
Республика Адыгея |
60,3 |
47056 |
|
Республика Дагестан |
469,5 |
134133 |
|
Республика Ингушетия |
10,5 |
5139 |
|
Кабардино-Балкарская Республика |
81,7 |
48059 |
|
Республика Калмыкия |
46,4 |
21677 |
|
Карачаево-черкесская Республика |
96,4 |
32493 |
|
Республика Северная Осетия – Алания |
356,5 |
43296 |
|
Краснодарский край |
2463,5 |
479549 |
|
Ставропольский край |
278,6 |
205580 |
|
Астраханская область |
321,9 |
106980 |
|
Волгоградская область |
782,9 |
206817 |
|
Ростовская область |
19140 |
299151 |
|
Республика Башкортостан |
14330,5 |
407013 |
|
Республика Марий Эл |
52,2 |
95617 |
|
Республика Мордовия |
304,8 |
70373 |
|
Республика Татарстан |
9739,4 |
477390 |
|
Удмуртская Республика |
934,9 |
180173 |
|
Чувашская Республика |
137,9 |
113170 |
|
Кировская область |
311 |
148026 |
|
Нижегородская область |
4833,2 |
294133 |
|
Оренбургская область |
502,8 |
234022 |
|
Пензенская область |
383,5 |
123940 |
|
Пермская область |
1300,9 |
302898 |
|
Самарская область |
7051,4 |
482883 |
|
Саратовская область |
1832,9 |
268971 |
|
Ульяновская область |
1448 |
125943 |
|
Курганская область |
75,5 |
93139 |
|
Свердловская область |
10187,3 |
580302 |
|
Тюменская область |
9666,7 |
1083475 |
|
Челябинская область |
4805,5 |
404407 |
|
Республика Алтай |
29,8 |
15278 |
|
Республика Бурятия |
817,4 |
91700 |
|
Республика Тыва |
14,8 |
14652 |
|
Республика Хакасия |
158,8 |
61889 |
|
Алтайский край |
405,2 |
191413 |
|
Красноярский край |
1320,6 |
383673 |
|
Иркутская область |
1053,6 |
339505 |
|
Кемеровская область |
1435,1 |
313617 |
|
Новосибирская область |
1682,8 |
302292 |
|
Омская область |
1774,7 |
190292 |
|
Томская область |
338 |
149647 |
|
Читинская область |
57 |
105245 |
|
Республика Саха (Якутия) |
408 |
220865 |
|
Приморский край |
1439 |
166236 |
|
Хабаровский край |
1933,3 |
248304 |
|
Амурская область |
108,5 |
141651 |
|
Камчатская область |
661,6 |
62198 |
|
Магаданская область |
236,8 |
45747 |
|
Сахалинская область |
247,9 |
97652 |
Источник данных: Регионы России. 2000. – М., 2001 г.
Для удобства работы составим отдельную таблицу, в которой регионы будут перенумерованы:
|
1. |
Белгородская область |
|
40. |
Ростовская область |
|
2. |
Брянская область |
|
41. |
Республика Башкортостан |
|
3. |
Владимирская область |
|
42. |
Республика Марий Эл |
|
4. |
Воронежская область |
|
43. |
Республика Мордовия |
|
5. |
Ивановская область |
|
44. |
Республика Татарстан |
|
6. |
Калужская область |
|
45. |
Удмуртская Республика |
|
7. |
Костромская область |
|
46. |
Чувашская Республика |
|
8. |
Курская область |
|
47. |
Кировская область |
|
9. |
Липецкая область |
|
48. |
Нижегородская область |
|
10. |
Московская область |
|
49. |
Оренбургская область |
|
11. |
Орловская область |
|
50. |
Пензенская область |
|
12. |
Рязанская область |
|
51. |
Пермская область |
|
13. |
Смоленская область |
|
52. |
Самарская область |
|
14. |
Тамбовская область |
|
53. |
Саратовская область |
|
15. |
Тверская область |
|
54. |
Ульяновская область |
|
16. |
Тульская область |
|
55. |
Курганская область |
|
17. |
Ярославская область |
|
56. |
Свердловская область |
|
18. |
Москва |
|
57. |
Тюменская область |
|
19. |
Республика Карелия |
|
58. |
Челябинская область |
|
20. |
Республика Коми |
|
59. |
Республика Алтай |
|
21. |
Архангельская область |
|
60. |
Республика Бурятия |
|
22. |
Вологодская область |
|
61. |
Республика Тыва |
|
23. |
Калининградская область |
|
62. |
Республика Хакасия |
|
24. |
Ленинградская область |
|
63. |
Алтайский край |
|
25. |
Мурманская область |
|
64. |
Красноярский край |
|
26. |
Новгородская область |
|
65. |
Иркутская область |
|
27. |
Псковская область |
|
66. |
Кемеровская область |
|
28. |
Санкт-Петербург |
|
67. |
Новосибирская область |
|
29. |
Республика Адыгея |
|
68. |
Омская область |
|
30. |
Республика Дагестан |
|
69. |
Томская область |
|
31. |
Республика Ингушетия |
|
70. |
Читинская область |
|
32. |
Кабардино-Балкарская Республика |
|
71. |
Республика Саха (Якутия) |
|
33. |
Республика Калмыкия |
|
72. |
Приморский край |
|
34. |
Карачаево-черкесская Республика |
|
73. |
Хабаровский край |
|
35. |
Республика Северная Осетия – Алания |
|
74. |
Амурская область |
|
36. |
Краснодарский край |
|
75. |
Камчатская область |
|
37. |
Ставропольский край |
|
76. |
Магаданская область |
|
38. |
Астраханская область |
|
77. |
Сахалинская область |
|
39. |
Волгоградская область |
|
|
|
Из исходной таблицы удалим столбец с названиями регионов, далее произведём над ней следующие преобразования.
В таблицу с данными введём следующие обозначения переменных:
x - кредиты, предоставленные предприятиям, организациям, банкам и физическим лицам, млн руб.
y - основные фонды в экономике (по полной балансовой (учетной) стоимости; на конец года), млн руб.
Получим следующую таблицу, которую сохраним в текстовом файле data.txt в рабочей папке среды R:
|
|
x |
y |
|
1. |
342,5 |
145787 |
|
2. |
275,4 |
113415 |
|
3. |
112,1 |
129272 |
|
4. |
274,5 |
211898 |
|
5. |
141,5 |
84550 |
|
6. |
129 |
105783 |
|
7. |
50,7 |
83716 |
|
8. |
401,3 |
124453 |
|
9. |
125,3 |
129114 |
|
10. |
5814,2 |
659675 |
|
11. |
58 |
64366 |
|
12. |
456,5 |
110379 |
|
13. |
192,2 |
125247 |
|
14. |
82,3 |
111642 |
|
15. |
319,1 |
175833 |
|
16. |
638,3 |
156543 |
|
17. |
727,9 |
185442 |
|
18. |
811856,3 |
1384509 |
|
19. |
41 |
90800 |
|
20. |
654,1 |
201201 |
|
21. |
103,3 |
198340 |
|
22. |
2411,2 |
136362 |
|
23. |
784,4 |
75707 |
|
24. |
244,7 |
223013 |
|
25. |
490,7 |
144824 |
|
26. |
221,8 |
65864 |
|
27. |
163,5 |
74695 |
|
28. |
41581 |
412221 |
|
29. |
60,3 |
47056 |
|
30. |
469,5 |
134133 |
|
31. |
10,5 |
5139 |
|
32. |
81,7 |
48059 |
|
33. |
46,4 |
21677 |
|
34. |
96,4 |
32493 |
|
35. |
356,5 |
43296 |
|
36. |
2463,5 |
479549 |
|
37. |
278,6 |
205580 |
|
38. |
321,9 |
106980 |
|
39. |
782,9 |
206817 |
|
40. |
19140 |
299151 |
|
41. |
14330,5 |
407013 |
|
42. |
52,2 |
95617 |
|
43. |
304,8 |
70373 |
|
44. |
9739,4 |
477390 |
|
45. |
934,9 |
180173 |
|
46. |
137,9 |
113170 |
|
47. |
311 |
148026 |
|
48. |
4833,2 |
294133 |
|
49. |
502,8 |
234022 |
|
50. |
383,5 |
123940 |
|
51. |
1300,9 |
302898 |
|
52. |
7051,4 |
482883 |
|
53. |
1832,9 |
268971 |
|
54. |
1448 |
125943 |
|
55. |
75,5 |
93139 |
|
56. |
10187,3 |
580302 |
|
57. |
9666,7 |
1083475 |
|
58. |
4805,5 |
404407 |
|
59. |
29,8 |
15278 |
|
60. |
817,4 |
91700 |
|
61. |
14,8 |
14652 |
|
62. |
158,8 |
61889 |
|
63. |
405,2 |
191413 |
|
64. |
1320,6 |
383673 |
|
65. |
1053,6 |
339505 |
|
66. |
1435,1 |
313617 |
|
67. |
1682,8 |
302292 |
|
68. |
1774,7 |
190292 |
|
69. |
338 |
149647 |
|
70. |
57 |
105245 |
|
71. |
408 |
220865 |
|
72. |
1439 |
166236 |
|
73. |
1933,3 |
248304 |
|
74. |
108,5 |
141651 |
|
75. |
661,6 |
62198 |
|
76. |
236,8 |
45747 |
|
77. |
247,9 |
97652 |
Считываем данные из файла data.txt:
data= read.table("data.txt", head=TRUE)
attach(data)
Поле корреляции (коррелограмму, диаграмму рассеяния) строится автоматически с помощью команды plot(x,y):
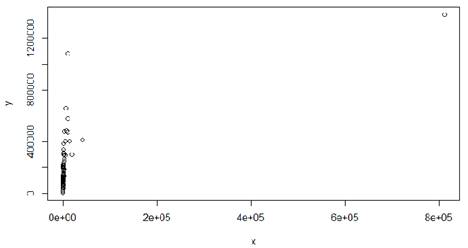
В правом верхнем углу мы видим точку, значительно отклоняющуюся от основной группы. Она соответствует данным по региону 18, то есть по Москве. Эту точку следует убрать.
Получается следующее поле корреляции:
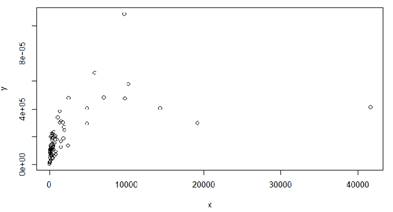
Убираем ещё две точки (по Санкт-Петербургу и Тюменской области).
Построенное поле корреляции с довольно отчётливой тенденцией:
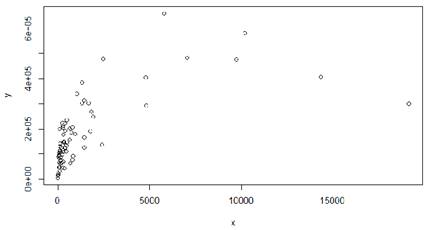
Ясно, что зависимость будет скорее квадратичной, но ни в коем случае не показательной и не гиперболической (эти зависимости являются либо строго возрастающими, либо строго убывающими).
Ищем зависимость в виде ![]()
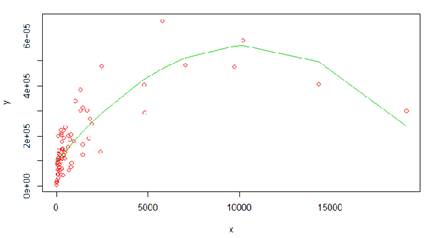
lm(formula = y ~ x + I(x^2))
Residuals:
Min 1Q Median 3Q Max
-150565 -51166 -5482 32731 189131
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 97020 10420 9.313 6.21e-14 ***
x 89050 7.588 1.735 2e-16 ***
I(x^2) -0.0043 0.00486 -8.778 6. 04e-13 ***
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 73050 on 71 degrees of freedom
Multiple R-squared: 0.7165, Adjusted R-squared: 0.7085
F-statistic: 89.7 on 2 and 71 DF, p-value: < 2.2e-16
Все коэффициенты a, b и c
значимы по критерию Стьюдента на уровне p-value < 0.001; это показывают ***
в столбце Coefficients) и сами значения p-value Pr(>|t|): ![]() для коэффициента a,
для коэффициента a, ![]() для коэффициента b и
для коэффициента b и ![]() для коэффициента с.
для коэффициента с.
Уравнение квадратичной
регрессии ![]()
Среднеквадратичное
отклонение (Adjusted R-squared) для данной модели составляет ![]() , то есть качество
модели достаточно высокое. Значимость среднеквадратичного отклонения
подтверждает и высокое значение F-статистики Фишера, равное 89.7, и общий
уровень значимости (определяемый по этой статистике): p-value:
, то есть качество
модели достаточно высокое. Значимость среднеквадратичного отклонения
подтверждает и высокое значение F-статистики Фишера, равное 89.7, и общий
уровень значимости (определяемый по этой статистике): p-value: ![]() , что много меньше
обычно достаточного на практике значения 0.001.
, что много меньше
обычно достаточного на практике значения 0.001.
Рассмотрим для сравнения остальные модели для нашей задачи.
Линейная модель
![]() :
:
> summary(lm(y~x))
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-345935 -66123 -16070 56229 368348
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.370e+05 1.344e+04 10.194 1.30e-15 ***
x 2.655e+01 3.763e+00 7.055 8.75e-10 ***
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 104800 on 72 degrees of freedom
Multiple R-squared: 0.4087, Adjusted R-squared: 0.4005
F-statistic: 49.77 on 1 and 72 DF, p-value: 8.752e-10
Среднеквадратичное
отклонение (Adjusted R-squared) для линейной модели составляет ![]() , качество модели неудовлетворительное.
, качество модели неудовлетворительное.
Экспоненциальная модель ![]()
> summary(lm(log(y)~x))
Call:
lm(formula = log(y) ~ x)
Residuals:
Min 1Q Median 3Q Max
-3.0420 -0.2631 0.1443 0.5378 1.1769
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.159e+01 9.841e-02 117.725 < 2e-16 ***
x 1.293e-04 2.756e-05 4.691 1.26e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.7672 on 72 degrees of freedom
Multiple R-squared: 0.2341, Adjusted R-squared: 0.2235
F-statistic: 22.01 on 1 and 72 DF, p-value: 1.259e-05
Среднеквадратичное
отклонение (Adjusted R-squared) для линейной модели составляет ![]() , качество модели
неудовлетворительное.
, качество модели
неудовлетворительное.
Степенная модель
![]()
> summary(lm(log(y)~log(x)))
Call:
lm(formula = log(y) ~ log(x))
Residuals:
Min 1Q Median 3Q Max
-1.65134 -0.29374 0.06559 0.39976 1.01151
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.17748 0.23953 38.31 <2e-16 ***
log(x) 0.43314 0.03853 11.24 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5281 on 72 degrees of freedom
Multiple R-squared: 0.6371, Adjusted R-squared: 0.632
F-statistic: 126.4 on 1 and 72 DF, p-value: < 2.2e-16
Среднеквадратичное
отклонение (Adjusted R-squared) для линейной модели составляет ![]() , качество модели
удовлетворительное, но хуже квадратичной модели.
, качество модели
удовлетворительное, но хуже квадратичной модели.
Гиперболическая
модель ![]()
> t=1/x
> summary(lm(y~t))
Call:
lm(formula = y ~ t)
Residuals:
Min 1Q Median 3Q Max
-151500 -76329 -42345 35332 454574
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 205773.84 16239.52 12.671 < 2e-16 ***
t -39.14 10.17 -3.848 0.000255 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 124100 on 72 degrees of freedom
Multiple R-squared: 0.1706, Adjusted R-squared: 0.159
F-statistic: 14.81 on 1 and 72 DF, p-value: 0.0002553
Среднеквадратичное
отклонение (Adjusted R-squared) для линейной модели составляет ![]() , качество модели очень плохое.
, качество модели очень плохое.
Множественная регрессия
Проведём анализ экономических результатах деятельности российских банков по следующим данным:
|
Банк |
Собственный капитал, % |
Средства частных лиц, % |
Кредиты предприятиям и организациям, млн руб. |
|
Сбербанк |
10 |
60 |
1073255 |
|
Внешторгбанк |
16 |
13 |
189842 |
|
Газпромбанк |
8 |
9 |
207118 |
|
Альфа-банк |
13 |
15 |
138518 |
|
Банк Москвы |
11 |
30 |
90757 |
|
Росбанк |
8 |
19 |
62388 |
|
Ханты-Мансийский банк |
3 |
5 |
4142 |
|
МДМ-банк |
12 |
9 |
51731 |
|
ММБ |
8 |
10 |
48400 |
|
Райффайзенбанк |
8 |
22 |
46393 |
|
Промстройбанк |
10 |
24 |
45580 |
|
Ситибанк |
11 |
12 |
33339 |
|
Уралсиб |
16 |
22 |
43073 |
|
Межпромбанк |
36 |
1 |
60154 |
|
Промсвязьбанк |
9 |
11 |
32761 |
|
Петрокоммерц |
15 |
26 |
23053 |
|
Номос-банк |
11 |
6 |
28511 |
|
Зенит |
14 |
10 |
25412 |
|
Русский стандарт |
19 |
7 |
3599 |
|
Транскредитбанк |
9 |
8 |
18506 |
|
Ак Барс |
23 |
19 |
23841 |
|
Глобэкс |
26 |
16 |
29420 |
|
Еврофинанс-Моснарбанк |
15 |
5 |
18114 |
|
Никойл |
23 |
11 |
13117 |
|
Автобанк-Никойл |
19 |
34 |
19135 |
|
Импэксбанк |
13 |
37 |
15047 |
|
Союз |
13 |
8 |
15507 |
|
БИН-банк |
12 |
20 |
24980 |
|
Возрождение |
9 |
49 |
20665 |
|
Гута-банк |
10 |
13 |
11556 |
|
Менатеп СПб |
11 |
16 |
7593 |
|
Коммерцбанк |
14 |
0 |
18158 |
|
ХКФБ |
11 |
6 |
28 |
|
Дойче банк |
13 |
7 |
2014 |
|
АБН Амро банк |
11 |
17 |
11044 |
|
ПЧРБ |
15 |
4 |
5415 |
|
МБРР |
12 |
8 |
14216 |
|
НРБ |
30 |
4 |
10408 |
|
Россельхозбанк |
21 |
14 |
13953 |
|
Сургутнефтегазбанк |
9 |
47 |
3254 |
|
Кредит Свисс |
16 |
0 |
8 |
|
Собинбанк |
25 |
15 |
15405 |
|
Траст |
25 |
3 |
2584 |
|
Запсибкомбанк |
12 |
26 |
8586 |
|
Судостроительный банк |
16 |
2 |
6811 |
|
Банк Санкт-Петербург |
10 |
28 |
11911 |
|
ИНГ банк |
16 |
6 |
11672 |
|
Балтийский банк |
12 |
50 |
11422 |
|
МИнБ |
11 |
37 |
11788 |
|
ВестЛБ Восток |
7 |
0 |
1169 |
|
Авангард |
19 |
12 |
11839 |
|
Российский кредит |
30 |
0 |
1406 |
|
Кредитагропромбанк |
9 |
14 |
5334 |
|
Инвестсбербанк |
17 |
26 |
6249 |
|
Сосьете Женераль Восток |
9 |
16 |
9128 |
|
Русь-банк |
17 |
3 |
9710 |
|
Пробизнесбанк |
12 |
9 |
6913 |
|
Национальный стандарт |
13 |
0 |
2233 |
|
ВБРР |
10 |
4 |
5881 |
|
Татфондбанк |
22 |
20 |
9897 |
|
МБСП |
13 |
13 |
5404 |
|
Абсолют банк |
12 |
10 |
7872 |
|
Визави |
39 |
1 |
7208 |
|
Центрокредит |
29 |
5 |
5097 |
|
Связь-банк |
18 |
8 |
3692 |
|
Россия |
12 |
15 |
5893 |
|
БНП Париба |
21 |
0 |
6638 |
|
МКБ |
18 |
13 |
6739 |
|
Газэнергопромбанк |
8 |
20 |
6295 |
|
Росевробанк |
15 |
13 |
5372 |
|
Северная казна |
9 |
46 |
4915 |
|
МДМ-банк СПб |
9 |
45 |
1222 |
|
РБР |
13 |
42 |
5031 |
|
Вэб-инвестбанк |
22 |
0 |
3784 |
|
Транскапиталбанк |
12 |
17 |
5660 |
|
Кредит Урал банк |
20 |
32 |
4621 |
|
Российский капитал |
30 |
21 |
6971 |
|
Пересвет |
11 |
12 |
5950 |
|
Сибакадембанк |
12 |
60 |
2878 |
|
Липецккомбанк |
7 |
25 |
3263 |
|
Калион Русбанк |
15 |
1 |
7142 |
|
Металлинвестбанк |
22 |
8 |
6631 |
|
Стройкредит |
12 |
14 |
1856 |
|
Оргрэсбанк |
22 |
4 |
4608 |
|
Югбанк |
9 |
42 |
6695 |
|
Славинвестбанк |
19 |
3 |
3105 |
|
Промторгбанк |
20 |
11 |
6954 |
|
Мастер-банк |
30 |
16 |
6036 |
|
Новикомбанк |
14 |
10 |
3950 |
|
УБРР |
10 |
59 |
6154 |
|
КМБ-банк |
11 |
19 |
2535 |
|
Центр-инвест |
13 |
38 |
5679 |
|
Челиндбанк |
13 |
45 |
3476 |
|
Конверсбанк |
21 |
2 |
3385 |
|
Таврический |
14 |
20 |
5920 |
|
Меткомбанк (Череповец) |
12 |
3 |
2153 |
|
Уралвнешторгбанк |
8 |
46 |
2490 |
|
Лефко-банк |
33 |
13 |
2836 |
|
Газбанк |
11 |
41 |
3708 |
|
Электроника |
27 |
9 |
3971 |
|
Девон-кредит |
20 |
47 |
4724 |
|
РосБР |
78 |
0 |
3949 |
|
МИБ |
34 |
5 |
5893 |
|
Экспобанк |
22 |
34 |
2708 |
|
Русский международный |
7 |
44 |
3910 |
|
Далькомбанк |
8 |
55 |
4432 |
|
Солидарность |
12 |
19 |
4442 |
|
Севергазбанк |
10 |
45 |
3009 |
|
Юниаструм банк |
18 |
38 |
2681 |
|
Нижегородский ПСБ |
21 |
37 |
4451 |
|
Локо-банк |
24 |
14 |
3181 |
|
Омский ПСБ |
11 |
66 |
3104 |
|
Финпромбанк |
11 |
4 |
3204 |
|
Алеф-банк |
18 |
2 |
739 |
|
Москоммерцбанк |
16 |
1 |
3866 |
|
Алмазэргиэнбанк |
2 |
4 |
244 |
|
Нефтяной |
28 |
10 |
4874 |
|
Челябинвестбанк |
15 |
38 |
2822 |
|
Фондсервисбанк |
14 |
11 |
4157 |
|
Академхимбанк |
14 |
6 |
3133 |
|
Банк Натексис |
8 |
0 |
2593 |
|
Русьуниверсалбанк |
41 |
2 |
3356 |
|
Инкасбанк |
19 |
14 |
3356 |
|
Инвестторгбанк |
17 |
26 |
2994 |
|
Межтопэнергобанк |
34 |
8 |
4662 |
|
СДМ-банк |
8 |
24 |
3490 |
|
СМП |
20 |
0 |
4114 |
|
АБД |
23 |
15 |
2477 |
|
Кедр |
11 |
49 |
2329 |
|
Евротраст |
20 |
6 |
2167 |
|
СКБ-банк |
19 |
40 |
2562 |
|
Интерпромбанк |
15 |
10 |
3185 |
|
Юникор |
14 |
17 |
2615 |
|
Солидарность (Москва) |
10 |
12 |
1831 |
|
Уралтрансбанк |
14 |
43 |
2863 |
|
Автовазбанк |
13 |
63 |
1487 |
|
Роспромбанк |
17 |
9 |
2795 |
|
Национальный космический |
20 |
7 |
1762 |
|
БПФ |
23 |
7 |
950 |
|
Петро-аэро-банк |
11 |
24 |
2493 |
|
Акибанк |
18 |
23 |
2974 |
|
Тюменьэнергобанк |
12 |
50 |
2230 |
|
БВТ |
21 |
7 |
2620 |
|
Тольяттихимбанк |
15 |
18 |
3640 |
|
Приморье |
9 |
23 |
2792 |
|
Меткомбанк |
9 |
30 |
1875 |
|
Нацторгбанк |
9 |
32 |
3281 |
|
Финансбанк |
9 |
16 |
2411 |
|
Ухтабанк |
14 |
50 |
1405 |
|
Московский капитал |
16 |
23 |
2625 |
|
ВИП банк |
15 |
4 |
698 |
|
Спурт |
29 |
11 |
3225 |
|
Саровбизнесбанк |
29 |
32 |
1414 |
|
Социнвестбанк |
20 |
31 |
3308 |
|
Фиа-банк |
9 |
42 |
2080 |
|
Югра |
10 |
56 |
1620 |
|
Центркомбанк |
23 |
0 |
3667 |
|
ФПБ |
15 |
5 |
2736 |
|
Казанский |
27 |
30 |
2537 |
|
Экспресс-Волга |
8 |
60 |
1365 |
|
Балтинвестбанк |
20 |
12 |
1611 |
|
Евразия-Центр |
26 |
13 |
2561 |
|
Трансинвестбанк |
28 |
20 |
672 |
|
Москомприватбанк |
10 |
28 |
731 |
|
Кузбассугольбанк |
16 |
49 |
702 |
|
Оптбанк |
32 |
5 |
2498 |
|
Красбанк |
32 |
9 |
1105 |
|
Стандарт банк |
22 |
0 |
894 |
|
Новосибирский ВТБ |
14 |
51 |
1128 |
|
Сибнефтебанк |
9 |
25 |
698 |
|
Дальневосточный банк |
11 |
31 |
1632 |
|
Ланта-банк |
16 |
27 |
830 |
|
Углеметбанк |
6 |
29 |
886 |
|
ДельтаКредит |
27 |
2 |
316 |
|
Гаранти банк-Москва |
30 |
9 |
1258 |
|
МАБ |
16 |
1 |
1549 |
|
НФК Уралсиб-Никойл |
23 |
0 |
2743 |
|
Капитал |
21 |
1 |
388 |
|
Русский банкирский дом |
20 |
26 |
2083 |
|
Уралпромстройбанк |
20 |
41 |
2272 |
|
Сибирьгазбанк |
9 |
65 |
794 |
|
Огни Москвы |
11 |
17 |
931 |
|
Пермкредит |
12 |
17 |
1842 |
|
Фора-банк |
8 |
17 |
1941 |
|
Славянский банк |
28 |
28 |
942 |
|
Региобанк |
11 |
49 |
1663 |
|
Евразбанк |
67 |
6 |
1367 |
|
НБР |
22 |
8 |
1052 |
|
БКФ |
14 |
5 |
476 |
|
Мак-банк |
10 |
48 |
902 |
|
Драгоценности Урала |
11 |
65 |
674 |
|
Русславбанк |
10 |
17 |
958 |
|
Росэксимбанк |
57 |
1 |
1338 |
|
МБР |
32 |
14 |
1938 |
|
МИА |
29 |
0 |
1924 |
|
Промэк-банк |
14 |
48 |
154 |
|
Альта-банк |
19 |
23 |
1381 |
|
ГКБ |
19 |
0 |
788 |
|
СГБ |
19 |
13 |
2324 |
|
Самарский кредит |
9 |
16 |
2146 |
|
Расчетно-кредитный банк |
12 |
10 |
295 |
|
Свердлсоцбанк |
12 |
42 |
2065 |
|
Интрастбанк |
26 |
14 |
2465 |
|
ПРБ |
31 |
12 |
1464 |
|
Ист бридж банк |
35 |
12 |
771 |
|
Эмпилс-банк |
14 |
3 |
978 |
Удалим из таблицы ненужные столбцы, пронумеруем банки и сохраним пронумерованный список банков в файл Номера банков.doc
Введем переменные:
x - Собственный капитал, %
y - Средства частных лиц, %
z - Кредиты предприятиям и организациям, млн руб.
Данные сохраним в файл data.txt
Пусть y и z – факторы, а z – признак.
Считываем данные из файла data.txt:
data= read.table("data.txt", head=TRUE)
attach(data)
Определим коэффициенты парной корреляции:
cor(data)
z x y
z 1.000
x -0.350 1.000
y -0.082 0.134 1.000
Они очень малы. Линейная зависимость признака от факторов практически отсутствует.
Определим частные корреляции:
>library(ggm)
> alpha=cor(data)
> parcor(alpha)
z x y
z 1.000
x -0.343 1.000
y -0.037 0.113 1.000
Построим модель
множественной линейной регрессии признака z на факторы x и y в виде ![]()
> summary(lm(z~x+y))
Call:
lm(formula = z ~ x + y)
Residuals:
Min 1Q Median 3Q Max
-18.266 -5.809 -1.157 3.873 56.966
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 21.05 0.9704 21.694 < 2e-16 ***
x -0.1961 0.003763 -5.211 4.61e-07 ***
y -4.379∙10-6 8.237∙10-6 -0.532 0.596
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 9.103 on 203 degrees of freedom
Multiple R-squared: 0.1238, Adjusted R-squared: 0.1152
F-statistic: 14.35 on 2 and 203 DF, p-value: 1.487∙10-6
Коэффициенты a = -0.196, b =-4.379∙10-6, c = 21.05.
Коэффициент b практически равен нулю. Согласно критерию Стьюдента он незначим, так как уровень значимости p-value = 0.596, что значительно превышает приемлемый уровень 0.001. Коэффициенты a и c значимы.
Коэффициент множественной
корреляции (Multiple R-squared) для данной модели составляет ![]() , то есть качество
данной модели неудовлетворительное.
, то есть качество
данной модели неудовлетворительное.
Значимость среднеквадратичного отклонения, равного 14.35, подтверждает и F-критерий Фишера, согласно которому общий уровень значимости (определяемый по этой статистике): p-value: .487∙10-6, что намного меньше обычно достаточного на практике значения 0.001.
Так как признак z от
фактора y практически не зависит, построим модель однофакторной линейной
регрессии признака z на факторы x в виде ![]()
> summary(lm(z~x))
Call:
lm(formula = z ~ x)
Residuals:
Min 1Q Median 3Q Max
-18.244 -5.800 -1.076 3.289 56.961
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 21.03883 0.96839 21.73 < 2e-16 ***
x -0.19877 0.03723 -5.34 2.47 ∙10-7 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 9.087 on 204 degrees of freedom
Multiple R-squared: 0.1226, Adjusted R-squared: 0.1183
F-statistic: 28.51 on 1 and 204 DF, p-value: 2.474∙10-7
Уравнение регрессии имеет вид z = -0.19877x + 21.03883.
Оба коэффициенты значимы,
однако среднеквадратичное отклонение (Adjusted R-squared) для данной модели
составляет ![]() , то есть качество данной модели неудовлетворительное.
, то есть качество данной модели неудовлетворительное.
Временны́е ряды
Исследуем динамику числа предприятий в Российской Федерации в 1995–2003 гг. на примере данных о Дальневосточном федеральном округе.
|
ЧИСЛО ПРЕДПРИЯТИЙ И ОРГАНИЗАЦИЙ |
|
|
|
|
|
|
|
|
|
|
|
(на конец года) |
|
|
|
|
|
|
|
|
|
|
|
|
1990 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
|
ДФО |
16804 |
114026 |
124008 |
129957 |
133223 |
138165 |
143186 |
149239 |
157128 |
167184 |
|
Республика
Саха |
2820 |
16536 |
17455 |
17999 |
17978 |
18304 |
19341 |
20260 |
21409 |
23914 |
|
Пpимоpский кpай |
3776 |
33521 |
36318 |
37826 |
38259 |
39764 |
41144 |
44404 |
47822 |
50502 |
|
Хабаpовский кpай |
3386 |
20799 |
23036 |
25030 |
26386 |
28310 |
29480 |
30957 |
33355 |
36396 |
|
Амуpская область |
2575 |
12272 |
13272 |
13499 |
13453 |
13674 |
14033 |
14330 |
14674 |
15124 |
|
Камчатская область |
1082 |
8114 |
8916 |
9534 |
10131 |
10767 |
11460 |
12177 |
12192 |
12672 |
|
Магаданская
|
1548 |
7465 |
8019 |
8379 |
8686 |
9030 |
9390 |
9738 |
9967 |
10149 |
|
Сахалинская
|
1617 |
11448 |
12895 |
13675 |
14231 |
13968 |
13801 |
12689 |
12862 |
13150 |
|
Еврейская АО |
... |
2745 |
2881 |
2732 |
2750 |
2870 |
2973 |
3077 |
3244 |
3499 |
|
Чукотский АО |
... |
1126 |
1216 |
1283 |
1349 |
1478 |
1564 |
1607 |
1603 |
1778 |
Для удобства обработки данных выделим список территориальных единиц отдельно и далее будем работать с их номерами по списку.
|
Республика Саха (Якутия) |
1. |
|
Пpимоpский кpай |
2. |
|
Хабаpовский кpай |
3. |
|
Амуpская область |
4. |
|
Камчатская область |
5. |
|
Магаданская область |
6. |
|
Сахалинская область |
7. |
|
Еврейская автономная область |
8. |
|
Чукотский автономный округ |
9. |
|
|
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
|
1. |
16536 |
17455 |
17999 |
17978 |
18304 |
19341 |
20260 |
21409 |
23914 |
|
2. |
33521 |
36318 |
37826 |
38259 |
39764 |
41144 |
44404 |
47822 |
50502 |
|
3. |
20799 |
23036 |
25030 |
26386 |
28310 |
29480 |
30957 |
33355 |
36396 |
|
4. |
12272 |
13272 |
13499 |
13453 |
13674 |
14033 |
14330 |
14674 |
15124 |
|
5. |
8114 |
8916 |
9534 |
10131 |
10767 |
11460 |
12177 |
12192 |
12672 |
|
6. |
7465 |
8019 |
8379 |
8686 |
9030 |
9390 |
9738 |
9967 |
10149 |
|
7. |
11448 |
12895 |
13675 |
14231 |
13968 |
13801 |
12689 |
12862 |
13150 |
|
8. |
2745 |
2881 |
2732 |
2750 |
2870 |
2973 |
3077 |
3244 |
3499 |
|
9. |
1126 |
1216 |
1283 |
1349 |
1478 |
1564 |
1607 |
1603 |
1778 |
Создадим матрицу процентов:
> proc = matrix(nrow =9, ncol = 9)
>for (k in 1:9){proc[,k]=data[,k]/sum(data[,k])*100}
>proc=round(proc,2)
> proc
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[1,] 14.50 14.08 13.85 13.49 13.25 13.51 13.58 13.63 14.30
[2,] 29.40 29.29 29.11 28.72 28.78 28.73 29.75 30.44 30.21
[3,] 18.24 18.58 19.26 19.81 20.49 20.59 20.74 21.23 21.77
[4,] 10.76 10.70 10.39 10.10 9.90 9.80 9.60 9.34 9.05
[5,] 7.12 7.19 7.34 7.60 7.79 8.00 8.16 7.76 7.58
[6,] 6.55 6.47 6.45 6.52 6.54 6.56 6.53 6.34 6.07
[7,] 10.04 10.40 10.52 10.68 10.11 9.64 8.50 8.19 7.87
[8,] 2.41 2.32 2.10 2.06 2.08 2.08 2.06 2.06 2.09
[9,] 0.99 0.98 0.99 1.01 1.07 1.09 1.08 1.02 1.06
|
1. |
7.25 |
7.04 |
6.92 |
6.75 |
6.62 |
6.75 |
6.79 |
6.81 |
7.15 |
|
2. |
14.70 |
14.64 |
14.55 |
14.36 |
14.39 |
14.37 |
14.88 |
15.22 |
15.10 |
|
3. |
9.12 |
9.29 |
9.63 |
9.90 |
10.24 |
10.29 |
10.37 |
10.61 |
10.89 |
|
4. |
5.38 |
5.35 |
5.19 |
5.05 |
4.95 |
4.90 |
4.80 |
4.67 |
4.52 |
|
5. |
3.56 |
3.59 |
3.67 |
3.80 |
3.90 |
4.00 |
4.08 |
3.88 |
3.79 |
|
6. |
3.27 |
3.23 |
3.22 |
3.26 |
3.27 |
3.28 |
3.26 |
3.17 |
3.04 |
|
7. |
5.02 |
5.20 |
5.26 |
5.34 |
5.05 |
4.82 |
4.25 |
4.09 |
3.93 |
|
8. |
1.20 |
1.16 |
1.05 |
1.03 |
1.04 |
1.04 |
1.03 |
1.03 |
1.05 |
|
9. |
0.49 |
0.49 |
0.49 |
0.51 |
0.53 |
0.55 |
0.54 |
0.51 |
0.53 |
Формируем матрицу процентов для региона в целом:
> years=c(1995:2003)
> region=c(1:9)
> for (k in 1:9){region[k]=sum(data[,k])/sum(data)*100}
> region
[1] 9.08 9.87 10.35 10.61 11.00 11.40 11.88 12.51 13.31
> plot(years, region)
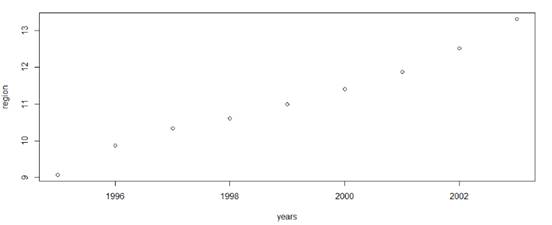
Доля малых предприятий в Дальневосточном федеральном округе монотонно увеличивается.
Рассмотрим возможные модели для нашей задачи.
Линейная модель ![]() :
:
> summary(lm(region~years))
Call:
lm(formula = region ~ years)
Residuals:
Min 1Q Median 3Q Max
-0.19039 -0.11956 -0.03672 0.19228 0.28511
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -944.74294 49.40579 -19.12 2.66e-07 ***
years 0.47817 0.02472 19.35 2.46e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1914 on 7 degrees of freedom
Multiple R-squared: 0.9816, Adjusted R-squared: 0.979
F-statistic: 374.3 on 1 and 7 DF, p-value: 2.457e-07
Мера определенности
(Multiple R-squared) для линейной модели составляет ![]() , качество модели высокое.
, качество модели высокое.
Уравнение имеет вид
region = -944.74 + 0.47817∙years
Экспоненциальная модель ![]()
> summary(lm(log(region)~years))
Call:
lm(formula = log(region) ~ years)
Residuals:
Min 1Q Median 3Q Max
-0.023117 -0.011279 -0.003857 0.014203 0.021515
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -83.835347 4.185390 -20.03 1.93e-07 ***
years 0.043140 0.002094 20.60 1.59e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.01622 on 7 degrees of freedom
Multiple R-squared: 0.9838, Adjusted R-squared: 0.9815
F-statistic: 424.5 on 1 and 7 DF, p-value: 1.592e-07
Мера определенности
(Multiple R-squared) для линейной модели составляет ![]() , качество модели высокое.
, качество модели высокое.
Уравнение ![]()
Степенная модель
![]()
> summary(lm(log(region)~log(years)))
Call:
lm(formula = log(region) ~ log(years))
Residuals:
Min 1Q Median 3Q Max
-0.023016 -0.011340 -0.003928 0.014304 0.021486
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -653.034 31.810 -20.53 1.63e-07 ***
log(years) 86.237 4.185 20.61 1.59e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.01622 on 7 degrees of freedom
Multiple R-squared: 0.9838, Adjusted R-squared: 0.9815
F-statistic: 424.6 on 1 and 7 DF, p-value: 1.592e-07
Мера определенности
(Multiple R-squared) для линейной модели составляет ![]() , качество модели высокое.
, качество модели высокое.
Уравнение![]()
Гиперболическая
модель ![]()
Call:
lm(formula = region ~ t)
Residuals:
Min 1Q Median 3Q Max
-0.19171 -0.11745 -0.03606 0.19274 0.28747
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.669e+02 4.958e+01 19.50 2.33e-07 ***
t -1.911e+06 9.912e+04 -19.28 2.52e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1921 on 7 degrees of freedom
Multiple R-squared: 0.9815, Adjusted R-squared: 0.9789
F-statistic: 371.6 on 1 and 7 DF, p-value: 2.52e-07
Среднеквадратичное
отклонение (Adjusted R-squared) для линейной модели составляет ![]() , качество модели высокое.
, качество модели высокое.
Уравнение ![]()
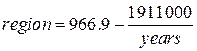
Все модели имеют высокое качество.
Наибольшее значение меры определенности имеет экспоненциальная зависимость, что дает основание рекомендовать именно ее для задач прогнозирования.
Заключение
В пособии рассмотрены конструкции самого́ языка R, которые были отобраны в результате практической обработки большого количества данных и необходимость в которых выявляется в первую очередь.
Как возникает необходимость в других конструкциях, продемонстрирована в пособии на примере решения СЛАУ и построении моделей в эконометрике.
Язык R можно с успехом применять в дальнейшем при изучении таких дисциплин, как численные методы, уравнения математической физики.
Особый интерес представляет построение баз данных. Эта тема не является предметом данного пособия, но особая эффективность и изящество конструкций языка R может быть продемонстрирована в курсах, посвященных СУБД. Первоначальные сведения об этом можно найти в [1].
Использованные источники
1. А.Б.Шипунов. Е.М. Балдин. П.А. Волкова. А.И. Коробейников. С.А. Назарова. С.В. Петров. В.Г. Суфиянов. – Наглядная статистика. Используем ¡ ! – М.: ДМК-Пресс. 2014.
2. Дьяконов А.Г. Справочник по базовым командам языка R. - http://alexanderdyakonov.narod.ru/upR.pdf
Скачано с www.znanio.ru
© ООО «Знанио»
С вами с 2009 года.
![]()