Задача 15. Решение Симплекс-методом.

Задача 15.  Мебельная фабрика для сборки столов и стульев привлекает к работе на 10 дней четырех столяров. Каждый столяр тратит 2 часа на сборку стола и 30 минут на сборку стула. Покупатели обычно приобретают вместе со столом от четырех до шести стульев. Доход от одного стола составляет 135 долл, и 50 долл. — от одного стула. На фабрике установлен 8-часовой рабочий день.

a)      Определите графически структуру производства (на 10 рабочих дней), которая максимизировала бы суммарный доход.

b)      Определите для найденного решения интервал оптимальности для отношения доходов на единицу продукции.

c)       Изменится ли найденное выше оптимальное решение, если доходность изготовления столов и стульев уменьшится на 10% ?

d)      Изменится ли найденное выше оптимальное решение, если доходность изготовления столов и стульев составит соответственно 120 и 26 долл, на единицу продукции?

Решение

a)

4 столяра соберут стол быстрее, за 0,5 часа, а стул за 0,125 часа. Поэтому, учитывая одинаковую производительность каждого и дополнительное условие отношения числа покупаемых столов к числу покупаемых стульев составим: 

Математическая модель задачи

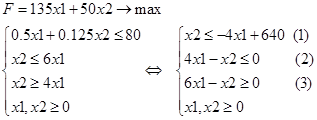
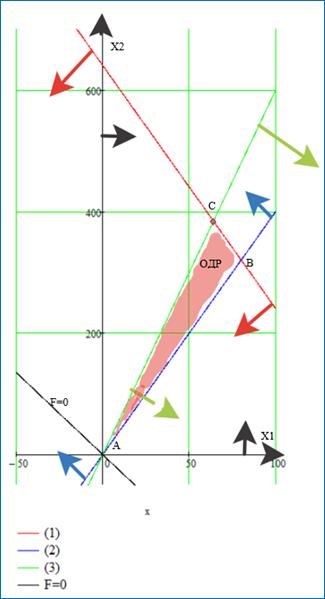
Построим область допустимых решений (ОДР), соответствующую ограничениям (1), (2), (3).   Для этого построим на  графике прямые, соответствующие ограничениям   (1), (2), (3),    прямую F = 0:  , и,  вектор с, со направленный вектору-градиенту grad F(0;0),    в точке (0;0),   с координатами  конца  (135;50).( на чертеже не показан)

Все прямые строим по точкам, придавая поочередно значения x1 = 0  - находим  x2,    и  наоборот. Например, для прямой (1): x1 = 0  => x2=640; x2 = 0  => x1=160; Получили две точки – через них построим прямую (1). 

Стрелками показываем полуплоскость, точки которой принадлежат множеству допустимых решений. (О. Д. Р).   Целевая функция, при движении линии уровня в направлении вектора градиента, параллельно самой себе, оставаясь при этом на ОДР, – достигает крайней точки ОДР в точке C  пересечения прямых (1) и (3).

В точке C (x1; x2)

Найдем координаты этой точки C (x1; x2):

-(4)x1+640=6x1  Û    x1=64;    Þ    x2=384;     C(64; 384)

 Þ   max F = 135*64 + 50*384 = 27840

Симплекс-метод:

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла (≤) вводим базисную переменную x₃. В 2-м неравенстве смысла (≤) вводим базисную переменную x₄. В 3-м неравенстве смысла (≥) вводим базисную переменную x₅ со знаком минус.
4x₁+x₂+x₃ = 640
4x₁-x₂+x₄ = 0
6x₁-x₂-x₅ = 0
Расширенная матрица системы ограничений-равенств данной задачи:

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Получаем новую матрицу:

Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Выразим базисные переменные через остальные:
x₃ = -4x₁-x₂+640
x₄ = -4x₁+x₂
x₅ = 6x₁-x₂
Подставим их в целевую функцию:
F(X) = 135x₁+50x₂
4x₁+x₂+x₃=640
4x₁-x₂+x₄=0
-6x₁+x₂+x₅=0
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Решим систему уравнений относительно базисных переменных: x₃, x₄, x₅
Полагая, что свободные переменные равны 0, получим первый опорный план:
X0 = (0,0,640,0,0)
Базисное решение называется допустимым, если оно неотрицательно.

Переходим к основному алгоритму симплекс-метода.
Итерация №0.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x₁, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения D_i по строкам как частное от деления: b_i / a_i1
и из них выберем наименьшее:
min (640 : 4 , 0 : 4 , - ) = 0
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (4) и находится на пересечении ведущего столбца и ведущей строки.

4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы. Вместо переменной x₄ в план 1 войдет переменная x₁.
Строка, соответствующая переменной x₁ в плане 1, получена в результате деления всех элементов строки x₄ плана 0 на разрешающий элемент РЭ=4. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₁ записываем нули.
Таким образом, в новом плане 1 заполнены строка x₁ и столбец x₁. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
СТЭ - элемент старого плана, РЭ - разрешающий элемент (4), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:

Получаем новую симплекс-таблицу:

Итерация №1.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения D_i по строкам как частное от деления: b_i / a_i2
и из них выберем наименьшее:
min (640 : 2 , - , - ) = 320
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (2) и находится на пересечении ведущего столбца и ведущей строки.

4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы. Вместо переменной x₃ в план 2 войдет переменная x₂.
Строка, соответствующая переменной x₂ в плане 2, получена в результате деления всех элементов строки x₃ плана 1 на разрешающий элемент РЭ=2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₂ записываем нули.
Таким образом, в новом плане 2 заполнены строка x₂ и столбец x₂. Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.
Представим расчет каждого элемента в виде таблицы:

Получаем новую симплекс-таблицу:

Итерация №2.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x₄, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения D_i по строкам как частное от деления: b_i / a_i4
и из них выберем наименьшее:
min (- , 80 : ¹/₈ , 160 : 1¹/₄ ) = 128
Следовательно, 3-ая строка является ведущей.
Разрешающий элемент равен (1¹/₄) и находится на пересечении ведущего столбца и ведущей строки.

4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы. Вместо переменной x₅ в план 3 войдет переменная x₄.
Строка, соответствующая переменной x₄ в плане 3, получена в результате деления всех элементов строки x₅ плана 2 на разрешающий элемент РЭ=1¹/₄. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₄ записываем нули.
Таким образом, в новом плане 3 заполнены строка x₄ и столбец x₄. Все остальные элементы нового плана 3, включая элементы индексной строки, определяются по правилу прямоугольника.
Представим расчет каждого элемента в виде таблицы:

Получаем новую симплекс-таблицу:

1. Проверка критерия оптимальности.
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:

Оптимальный план можно записать так:
x₁ = 64, x₂ = 384
F(X) = 135*64 + 50*384 = 27840

Вывод: Целевая функция имеет максимум -  max F =27840 в точке C (64; 384)

b)

Функция достигает своего оптимума в точке, которая является пересечением прямых (0.5x₁+0.125x₂=80) и (6x₁-x₂=0). При изменении коэффициентов целевой функции эта точка останется точкой оптимального решения до тех пор, пока угол наклона линии z будет лежать между углами наклона этих прямых. Алгебраически это можно записать:
    при условии c₁ ≠ 0         или            при условии c₂ ≠ 0
Это две системы неравенств, определяющих интервал оптимальности.
При c₂ = 50:        или        -300 ≤ c₁ ≤ 200     (с1 столы)
При c₁ = 135:      или      ^-45/₂ ≤ c₂ ≤ 33.75    (с2 стулья)

с) Нет, не изменится. Рассмотрим прямую F=0 <=> x2= -135/50*x1. При уменьшении доходности на 10% числитель и знаменатель помножаются на одинаковый коэффициент равный 0,9 =>  x2= -(135*0.9)/(50*0.9)*x1   <=>  x2= -135/50*x1

Т.к. коэффициент у F=0 не меняется то крайняя точка С не изменится.

Сама же целевая функция измениться пропорционально, т.к. множитель у обоих коэффициентов одинаков,  и станет равной:  F* = 0.9*F=27840*0.9 = 25056

d)  Да, измениться, т.к. коэффициент у прямой F=0 станет больше (по модулю) чем у прямой (1).   k1 = -4,  а  к2=-120/25=-4,8. Поэтому прямая F=0  «проскочит» точку А и остановится в точке B=(x1b; x2b), координаты которой найдем из уравнения:

-4x1+640=4x1 => x1=64/8=80;   x2=4x1=320;  B(80;320)

F(B)=120*80+25*320=17600 – новое значение целевой функции