Поделиться
Задача по программированию Вычислить xn по алгоритму быстрого возведения в степень.docx
Формулировка. Даны натуральные числа x и n. Вычислить xn, используя алгоритм быстрого возведения в степень:
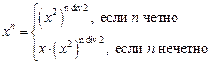
Решение. Разберем этот пока неясный алгоритм, представленный в нашей задаче лишь единственной формулой. Легко понять, что указанное равенство имеет место: например, 34 = 34 div 2 = (32)2 = 92 = 81. Другой пример: 45 = 4 * (42)5 div 2 = 4 * (42)2 = 4 * 162 = 4 * 256 = 1024. Причем если выражение со степенью нельзя в один шаг преобразовать таким образом, то необходимо продолжить преобразование выражения вплоть до получения конечного ответа. Однако как теперь реализовать эту схему?
Рассмотрим пример немного сложнее. Вычислим 47 = 4 * (42)3 = 4 * (16)3 = 4 * 16 * (162)1 = 4 * 16 * 256 = 16384. Стоит обратить внимание на то, что на каждом шаге при вычислении изменяется только единственное обрабатывающееся число, а остальные множители выносятся однократно и необходимы только для получения ответа в последнем действии.
Чтобы исключить их из рассмотрения, при нечетном текущем числе n мы будем домножать на них некоторую промежуточную переменную r, поначалу равную 1 (кстати, нечетность числа в Pascal определяет функция odd), затем (уже независимо от условий) возведем в квадрат текущее x и разделим n на 2 с отбрасыванием остатка. При повторении этих действий на некотором шаге n обязательно станет равным 1. Это происходит потому, что деление любого нечетного числа a на 2 с отбрасыванием остатка равносильно делению на двойку числа (a – 1), которое является четным, и при делении, двигаясь по цепочке четных чисел, мы всегда придем к единице. Условие n = 1 и будет окончанием цикла с предусловием. По выходе из цикла необходимо будет в качестве ответа вывести последнее значение x, умноженное на r.
Теперь алгоритм на естественном языке:
1) Ввод x и n;
2) Присваивание переменной r числа 1;
1) Запуск цикла с предусловием n < > 1. В цикле:
1. Если n нечетно, домножаем r на x;
2. Переменной x присваиваем значение x * x;
3. Переменной n присваиваем результат от деления этой переменной на 2 с отбрасыванием остатка;
3) Вывод выражения x * r.
Код:
|
1. program FastExponentiation; 2. 3. var 4. x, n, r: word; 5. 6. begin 7. readln(x, n); 8. r := 1; 9. while n <> 1 do begin 10. if odd(n) then r := r * x; 11. x := x * x; 12. n := n div 2 13. end; 14. writeln(x * r) 15. end. |
Из анализа данного алгоритма известно, что его асимптотическая сложность порядка O(log2n).
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
