Задачи на клетчатой бумаге

Задачи на клетчатой бумаге. Формула Пика.

Задачи на бумаге в клетку помогают как можно раньше формировать геометрические представления у школьников на разнообразном материале. При решении таких задач возникает ощущение красоты, закона и порядка в природе.

При решении задач на клетчатой бумаге ученикам не понадобится знание основ планиметрии, а будет нужна именно смекалка, геометрическое воображение и достаточно простые геометрические сведения, которые известны всем.

Наш сюжет будет разворачиваться на обычном листке клетчатой бумаги.[1]

Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах (рис. 1) и найдем его площадь. Искать её можно по-разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площадь и сложить.

Но тут нас ждёт много хлопот (попробуйте!). Давайте «схитрим»:

вычислим площадь заштрихованной фигуры, которая «дополняет» наш

Рис. 1

многоугольник до прямоугольника АВСD, и вычтем её из площади прямоугольника. Заштрихованная фигура легко разбивается на прямоугольники и прямоугольные треугольники, и её площадь вычисляется без усилий.

Итак, хотя многоугольник и выглядел достаточно просто, для вычисления его площади нам пришлось потрудиться. А если бы многоугольник выглядел более причудливо?

Оказывается площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.

Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (рис. 2).

Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую

Рис. 2

клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна

S = В +  + 4 ·  = В +  - 1 .

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу S = В +  - 1 .

Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки!

Это и есть формула Пика.

Задача 1. Проверить формулу Пика для многоугольника на рисунке 1.

Решение.

В = 14, Г = 8. По формуле Пика: S = В +  - 1 .

S = 14 + 8/2 – 1 = 17

Ответ: 17 кв. ед.

Можно убедиться в том, что формула Пика верна для всех рассмотренных примеров.

Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

Попробуйте вычислить площади многоугольников с рисунка 3, используя формулу Пика. Правда ведь, легко получается!

Рис. 3

Рассмотрим ещё некоторые задачи на клетчатой бумаге с клетками размером 1 см 1 см

Задача 2.[3]

Найдите площадь прямоугольника АВСD (рис.4).

Решение. По формуле Пика: S = В +  - 1 .

В = 8, Г = 6

S = 8 + 6/2 – 1 = 10 (см²)

Рис. 4 Ответ: 10 см².

Задача 3. Найдите площадь параллелограмма АВСD (рис.5)

Решение. По формуле Пика: S = В +  - 1 .

В = 6, Г = 6

S = 6 + 6/2 – 1 = 8 (см²)

Ответ: 8 см².

Рис. 5

Задача 4. Найдите площадь треугольника АВС (рис.6)

Решение. По формуле Пика: S = В +  - 1 .

В = 6, Г = 5

S = 6 + 5/2 – 1 = 7,5 (см²)

Ответ: 7,5 см².

Рис. 6

Задача 5. Найдите площадь четырёхугольника АВСD (рис. 7)

Решение. По формуле Пика: S = В +  - 1 .

В = 5, Г = 7

S = 5 + 7/2 – 1 = 7,5 (см²)

Ответ: 7,5 см².

Рис. 7

Согласитесь, рассмотренные задания аналогичны заданию В из вариантов контрольно-измерительных материалов ЕГЭ по математике.

Например:

Задача 6.[2] В. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (рис. 8). Найдите его площадь в квадратных сантиметрах.

Решение. По формуле Пика: S = В +  - 1 .

В = 12, Г = 6

S = 12 + 6/2 – 1 = 14 (см²)

Ответ: 14

Рис. 8

Задача 7. В. На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (рис. 9). Найдите ее площадь в квадратных сантиметрах.

Решение. Воспользуемся формулой Пика:

В = 12, Г = 17

S = 12 + 17/2 – 1 = 19,5 (см²)

Ответ: 19,5

Рис. 9

Поможет нам формула Пика и для решения геометрических задач с практическим содержанием.

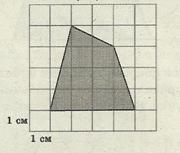
Задача 8.[4] Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м (рис. 10)

Решение. Найдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S = В +  - 1

В = 8, Г = 7. S = 8 + 7/2 – 1 = 10,5 (см²)

1 см² - 200² м²; S = 40000 · 10,5 = 420 000 (м²)

Ответ: м²

Рис. 10

Задача 9. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м. (рис. 11)

Решение. Найдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S = В +  - 1

В = 7, Г = 4. S = 7 + 4/2 – 1 = 8 (см²)

1 см² - 200² м²; S = 40000 · 8 = 320 000 (м²)

Ответ: м²

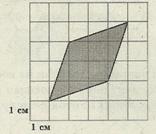Рис. 11

Получить полный текс

Скачано с www.znanio.ru