Задачи на равенство треугольников по первому признаку

Задачи на равенство треугольников по первому признаку - сторона-угол-сторона

Задача 1
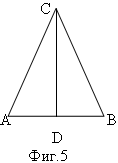
Треугольник ABC - равнобедренный, СD - биссектриса к основанию АВ.
Докажите, что ACD = BCD
Доказательство:
Докажем, что два треугольника равны по первому признаку. Из условия мы имеем, что
1. ∠ACD = ∠DCB (CD - биссектриса);
2. AC = BC ( треугольник АВС - равнобедренный);
3. CD принадлежит обоим треугольникам.
Тогда, треугольники ACD и BCD имеют две равные стороны и угол между ними.
Поэтому треугольники △ACD и △BCD - равны.

Задача 2

Докажите, что высота, биссектриса и медиана, проведённые  к основанию равнобедренного треугольника, совпадают.
Доказательство:
Из предыдущей задачи мы имеем, что CD это биссектриса в равнобедренном треугольнике АВС, и мы доказали, что треугольники ACD и BCD равны. Из равенства следует, что угол ADC = CDB но они но они являются смежными, следовательно, их сумма равна 180°, отсюда угол ADC = CDB = 90°, что показывает, что CD это высота. Из равенства двух треугольников мы имеем, что AD = BD,  значит CD является медианой.