Задачи по теории вероятности и статистике по теме "Сочетания. Факториал"

Задачи по теории вероятности и статистике по теме «Сочетания. Факториа».

1.       В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?

2.       Из лаборатории, в которой работают заведую­щий и 10 сотрудников, надо отправить 5 человек в командировку. Сколькими способами это можно сделать, если: а) заведующий лабораторией должен ехать в командировку;  б) заведующий лабораторией должен остаться?

3.       В библиотеке читателю предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими cпocoбами он может выбрать из них 3 книги и 2 журнала?

4.       В отделе работают 5 ведущих и 8 старших на­учных сотрудников. В командировку надо послать двух ведущих и трех старших научных сотрудников. Сколькими способами может быть сделан выбор сотрудников, которых надо послать в команди­ровку?

5.       Сколькими способами группу из 12 человек можно разбить на две группы: а) по 4 и 8 человек; б) по 5 и 7 чело­век?

1.                 В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?

    Решение.  Выбор из 8 по 3 без учета порядка: = 56 способов.

    Ответ: 56 способов.

2.  Из лаборатории, в которой работают заведую­щий и 10 сотрудников, надо отправить 5 человек в командировку. Сколькими способами это можно сделать, если:

     а)  заведующий лабораторией должен ехать в командировку;

     б)  заведующий лабораторией должен остаться?

     Решение:    Из 11 человек 5 должны поехать в командировку.

     а) Заведующий едет, нужно выбрать еще 4 из 10 оставшихся:способов.

     в) Заведующий остается, нужно выбрать 5 из 10 сотрудников: способа.      Ответ: а) 210 способов; б) 252 способа

3. В библиотеке читателю предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими cпocoбами он может выбрать  из них 3 книги и 2 журнала?

     Решение: Нужно сделать два выбора: 3 книги из 10 ( способов) и 2 журнала из 4 (  способов) ; порядок выбора не имеет значения. Каждый  выбор книг может сочетаться с каждым выбором журналов, поэтому общее число способов выбора по правилу произведения равно:  способов.       Ответ: 720 способов.

4.  Сколькими способами группу из 12 человек можно разбить на две группы: а) по 4 и 8 человек; б) по 5 и 7 чело­век?

     Решение: Количество способов разбиения множества на две части равно количеству способов формирования одной из частей (любой). По­скольку порядок расположения элементов не учитывается, имеем:

     а)способов разбиения на 4 и 8 элементов.

     б)  способов разбиения на 5 и 7 элементов.

      Ответ: а) 495 способов; б) 792 способа.

5. В отделе работают 5 ведущих и 8 старших на­учных сотрудников. В командировку надо послать двух ведущих и трех старших научных сотрудников. Сколькими способами может быть сделан выбор сотрудников, которых надо послать в команди­ровку?

     Решение: Выбор из двух разных совокупностей без учета порядка; каж­дый вариант выбора из первой совокупности (их С) может соче­таться с каждым вариантом выбора из второй совокупности (их С), по правилу произведения общее число способов выбрать со­трудников, уезжающих в командировку, равно:

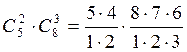= 560 способов.       Ответ: 560 способов.

Самостоятельная работа.

1. На двери два замка. Вероятность того, что первый замок закрыт, равна 0,9. Вероятность того, что второй замок закрыт, равна 0,8. Вероятность того, что оба замка закрыты, равна 0,72. Найдите вероятность того, что: а) закрыт хотя бы один замок; б) оба замка открыты;

в) дверь заперта только на первый замок; г) дверь заперта только на один замок.

2. У фирмы такси имеется всего два автобуса. Клиент хочет срочно заказать один автобус. Вероятность того, что в этот момент первый автобус свободен, равна 0,6. Такова же вероятность, что свободен второй автобус. Вероятность того, что свободны оба автобуса, равна 0,36. Найдите вероятность того, что в момент заказа: а) свободен хотя бы один автобус; б) ни один автобус не свободен; в) свободен только второй автобус;

г) свободен только один из автобусов.

3. Клиент хочет записаться на обслуживание в автосервис в один из двух дней –– в субботу или в воскресенье. Вероятность того, что в субботу автосервис сможет принять клиента, равна 0,8. Вероятность того, что автосервис сможет принять клиента в воскресенье, равна 0,9. Вероятность того, что автосервис сможет принять клиента в любой из дней, равна 0,72. Найдите вероятность того, что сервис: а) сможет принять клиента хотя бы в один из выходных; б) не сможет принять клиента ни в один из выходных; в) сможет принять клиента только в субботу; г) сможет принять клиента только в воскресенье.

4. В некоторой игре заняты двое игроков. Игра может окончиться победой одного из них либо вничью. Вероятность того, что первый игрок не проиграет, равна 0,4. Вероятность того, что не проиграет второй игрок, равна 0,7. Найдите вероятность того, что игра окончится вничью.

5. Двое играют в некоторую игру. Игра может окончиться победой одного из игроков либо вничью. Вероятность проигрыша первого игрока равна 0,3. Вероятность проигрыша второго игрока равна 0,5. Найдите вероятность того, что игра окончится победой одного из игроков.

6. Двое играют в шашки. Силы игроков равны, но ничья наступает с вероятностью 0,4. Найдите вероятность того, что выиграет первый игрок

7. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в каждом одном автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,18. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах           

8. В небольшом магазине работают два продавца –– Василий и Сергей. Каждый из них может быть занят с клиентом с вероятностью 0,4. При этом они могут быть заняты одновременно с вероятностью 0,3. Найдите вероятность того, что: а) занят только Василий, а Сергей свободен; б) занят только один из них, а другой свободен; в) оба свободны.                  

Самостоятельная работа(ответы).

1. На двери два замка. Вероятность того, что первый замок закрыт, равна 0,9. Вероятность того, что второй замок закрыт, равна 0,8. Вероятность того, что оба замка закрыты, равна 0,72. Найдите вероятность того, что: а) закрыт хотя бы один замок;

б) оба замка открыты;

в) дверь заперта только на первый замок;

г) дверь заперта только на один замок.   (а) 0,98   б) 0,02, в) 0,18  г) 0,26)

2. У фирмы такси имеется всего два автобуса. Клиент хочет срочно заказать один автобус. Вероятность того, что в этот момент первый автобус свободен, равна 0,6. Такова же вероятность, что свободен второй автобус. Вероятность того, что свободны оба автобуса, равна 0,36. Найдите вероятность того, что в момент заказа: а) свободен хотя бы один автобус; б) ни один автобус не свободен; в) свободен только второй автобус;

г) свободен только один из автобусов.   ( а) 0,84  б) 0,16 в) 0,24  г) 0,48)

3. Клиент хочет записаться на обслуживание в автосервис в один из двух дней –– в субботу или в воскресенье. Вероятность того, что в субботу автосервис сможет принять клиента, равна 0,8. Вероятность того, что автосервис сможет принять клиента в воскресенье, равна 0,9. Вероятность того, что автосервис сможет принять клиента в любой из дней, равна 0,72. Найдите вероятность того, что сервис: а) сможет принять клиента хотя бы в один из выходных; б) не сможет принять клиента ни в один из выходных; в) сможет принять клиента только в субботу; г) сможет принять клиента только в воскресенье.

(а) 0,98  б) 0,02  в) 0,08 г) 0,18)

4. В некоторой игре заняты двое игроков. Игра может окончиться победой одного из них либо вничью. Вероятность того, что первый игрок не проиграет, равна 0,4. Вероятность того, что не проиграет второй игрок, равна 0,7. Найдите вероятность того, что игра окончится вничью. (ответ 0,1)

5. Двое играют в некоторую игру. Игра может окончиться победой одного из игроков либо вничью. Вероятность проигрыша первого игрока равна 0,3. Вероятность проигрыша второго игрока равна 0,5. Найдите вероятность того, что игра окончится победой одного из игроков.  ( р = 0,8)

6. Двое играют в шашки. Силы игроков равны, но ничья наступает с вероятностью 0,4. Найдите вероятность того, что выиграет первый игрок (р = 0,3)

7. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в каждом одном автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,18. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах            (0,58)

8. В небольшом магазине работают два продавца –– Василий и Сергей. Каждый из них может быть занят с клиентом с вероятностью 0,4. При этом они могут быть заняты одновременно с вероятностью 0,3. Найдите вероятность того, что: а) занят только Василий, а Сергей свободен; б) занят только один из них, а другой свободен; в) оба свободны.                   а) 0,1; б) 0,2; в) 0,5