
Задачи на составление уравнений
Задача № 1
Бригада рабочих должна была выполнить заказ за 5 дней. Ежедневно превышая норму на 18 деталей, она за 3,5 дня работы не только выполнила задание, но и изготовила 27 деталей сверх плана. Сколько деталей изготовила бригада?
Задача № 2
В упаковке находится 2 кг смеси сухофруктов. Чернослива в этой смеси в 1,6 раза больше, чем яблок, а изюма на 0,2 кг больше, чем яблок. Сколько яблок, чернослива и изюма в упаковке в отдельности?
Задача № 3
Каждый из двух пешеходов прошел по 6 км. Скорость первого пешехода на 3 км/ч больше скорости второго, а поэтому время, которое был в пути первый пешеход, отличается от времени второго пешехода на 1 час. Сколько времени был в пути первый пешеход?
Задача № 4
Из пунктов А и В, расстояние между которыми 19 км, вышли одновременно навстречу друг другу два пешехода и встретились в 9 км от пункта А. Найдите скорость каждого, если известно, что пешеход, вышедший из А, шел со скоростью на 1км/ч большей, чем второй пешеход, и сделал в пути получасовую остановку.
Задача № 5
Катер, собственная скорость которого 8 км/ч, прошел по реке расстояние, равное 15 км/ч, по течению и такое же расстояние против течения. Найдите скорость течения реки, если время, затраченное на весь путь, равно 4 ч.
Задача № 6
Зарплата лаборанта составляла 100 рублей в месяц, после двух последовательных повышений на одно и то же число процентов она стала составлять 121 р. На сколько процентов каждый раз повышалась зарплата лаборанта?
Задача № 7
За 3 м одной ткани и 3 м другой заплатили 90 рублей. Сколько стоит 1 м каждой ткани, если 9 м первой ткани стоят столько же, сколько 6 м второй ткани?
Задача № 8
В двух корпусах пансионата было 720 мест для отдыхающих. После реконструкции в первом корпусе число мест увеличилось на 15 %, а во втором – на 10 %. Сколько мест для отдыхающих стало в каждом корпусе, если общее число мест в обоих корпусах увеличилось на 80?
Задача № 1
Р е ш е н и е.
Обозначим через х количество деталей, которое бригада планировала изготавливать за один день. Тогда, выполнив заказ за 5 дней, она по плану должна была изготовить 5х деталей, но превышая норму, бригада изготовляла в день (х + 18) деталей, значит, за 3,5 дня она сделала (х + 18) · 3,5 деталей. По условию задачи бригада за 3,5 дня не только выполнила задание, но и изготовила 27 деталей сверх плана. С учетом этого составляем уравнение: (х + 18) · 3,5 = 5х + 27.
Решаем полученное уравнение (х + 18) · 3,5 = 5х + 27.
5х – 3,5х = 63 – 27; 1,5х = 36; х = 24. Значит, бригада планировала изготовлять в день по 24 детали, а делала 24 + 18 = 42 детали; тогда за 3,5 дня она сделала 42 · 3,5 = 147 деталей.
О т в е т: 147 деталей.
Задача № 2
Р е ш е н и е.
Пусть в упаковке х кг яблок, тогда чернослива в ней 1,6х кг, а изюма – (х + 0,2) кг. Вся смесь имеет массу 2 кг.
Уравнение: х + 1,6х + х + 0,2 = 2.
Решение уравнения: 3,6х = 2 – 0,2,
3,6х = 1,8,
х = 0,5.
В упаковке 0,5 кг яблок, 0,7 кг изюма и 0,8 кг чернослива.
О т в е т: 0,5 кг; 0,7 кг; 0,8 кг.
Задача № 3
Р е ш е н и е:
Пусть первый пешеход был в пути х часов, тогда 6 км он прошел за км/ч. Так как скорость первого пешехода была больше скорости второго, то второй пешеход на такое же расстояние времени затратил, по условию задачи, на 1 час больше. Значит он в пути был (х + 1) часов и его скорость была ровна км/ч.
По
условию задачи скорость первого пешехода была больше скорости второго пешехода
на 3 км/ч. С учетом этого составляем уравнение:![]() . (Уравнение также можно записать в
виде
. (Уравнение также можно записать в
виде ![]() , или
, или ![]() .
.
Решаем полученное уравнение:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;
2 = х(х + 1);
![]() + х – 2 =
0;
+ х – 2 =
0;
D = 1 + 4 · 2 = 9;
![]() ;
;
х1 = 1; х2 = –2.
При х1 = 1 х(х+1) ? 0; при х2 = –2 х(х + 1) ? 0. значит х1 = 1 и х2 = –2 – корни уравнения, но значение х2 = –2 условию задачи не удовлетворяет, так как время движения пешехода не может быть выражено отрицательным числом. Следовательно, х = 1.
О т в е т: первый пешеход был в пути 1 час.
Задача № 4
Р е ш е н и е.
Обозначим скорость пешехода, вышедшего из пункта А, – х
км/ч, тогда скорость второго пешехода – (х – 1) км/ч. Первый пешеход был в пути
![]() ч,
а второй –
ч,
а второй – ![]() ч.
По условию задачи пешеходы вышли одновременно и встретились, но второй пешеход
делал остановку на ч, следовательно, можно составить
ч.
По условию задачи пешеходы вышли одновременно и встретились, но второй пешеход
делал остановку на ч, следовательно, можно составить![]() уравнение: .
уравнение: .
Решение
уравнения:Решение
уравнения: ![]() , НОЗ: 2х(х
– 1).
, НОЗ: 2х(х
– 1).
20х – 18(х – 1) = х(х – 1),
20х – 18х + 18 = х2 – х,
х2– 3х – 18 = 0,
D = 9 + 4 · 18 = 91,
![]() ,
,
х1 = 6, х2 = –3.
При х = 6 2х(х – 1) ? 0, при х = –3 2х(х – 1) ? 0, значит, х = 6 и х = –3 – корни составленного уравнения, но х = –3 не удовлетворяет условию задачи, остается х = 6. Скорость пешехода, вышедшего из пункта А – 6 км/ч, скорость второго 6 – 1 = 5 км/ч.
О т в е т: 6 км/ч, 5 км/ч.
Задача № 5
Р е ш е н и е.
Задача № 5
Р е ш е н и е.
Пусть хкм/ч
– скорость течения реки, тогда скорость катера по течению (8 + х) км/ч,
а против течения – (8 – х) км/ч, и время движения по течению ![]() ч, а против
течения
ч, а против
течения ![]() ч. По условию
задачи время, затраченное на весь путь, равно 4 ч.
ч. По условию
задачи время, затраченное на весь путь, равно 4 ч.
Уравнение: ![]() .
.
Решение уравнения:
![]() ;НОЗ: (8 + х)(8
– х),
;НОЗ: (8 + х)(8
– х),
15(8 – х) + 15(8 + х) = 4(64 – х2),
120 – 15х + 120 + 15х = 256 – 4х2,
4х2 – 16 = 0,
х2– 4 = 0,
(х – 2)(х + 2) = 0,
х1 = 2, х2= –2.
При х = 2 (8 + х)(8 – х) ≠ 0, при х = –2 (8 + х)(8 – х) ≠ 0, значит х = 2 и х = –2 – корни уравнения, но х = –2 условию задачи не удовлетворяет, следовательно, х = 2, т. е. скорость течения реки 2 км/ч.
О т в е т: 2 км/ч.
Задача № 6
Р е ш е н и е.
Задача № 6
Р е ш е н и е.
Пусть зарплата
лаборанта повышалась каждый раз на х %, тогда первый раз она повысилась
на 100 : 100 · х = х руб. и стала составлять (100 + х)
рублей. Во второй раз она повысилась на (100 + х) : 100 · х
рублей и стала составлять после этого ![]() рублей, достигнув, по условию задачи,
размера 121 рубль в месяц. С учетом этого составляем уравнение:
рублей, достигнув, по условию задачи,
размера 121 рубль в месяц. С учетом этого составляем уравнение: ![]() .
.
Решаем полученное уравнение:
10000 + 100х + 100х + х2 = 12100;
х2 + 200х – 2100 = 0;
![]() ;
;
![]() ;
;
х1 = –210; х2 = 10.
Значит, х = –210 и х = 10 – корни уравнения, но значение х = –210 условию задачи не удовлетворяет, так как является отрицательным числом. Следовательно, зарплата лаборанта дважды повышалась на 10 %.
О т в е т: 10 %.
Задача № 7
Р е ш е н и е.
Пусть один метр первой ткани стоит х рублей, а один метр второй ткани стоит у рублей. Тогда 3 м первой ткани стоят 3х рублей, а 3 м второй ткани стоят 3у рублей. Так как по условию задачи за 3 м одной ткани и 3 м второй заплатили 90 рублей, составляем уравнение: 3х + 3у = 90.
Поскольку 9 м первой ткани стоят 9х рублей, а 6 м второй ткани стоят 6у рублей, а по условию задачи 9 м первой ткани стоят столько же, сколько 6 м второй ткани, составляем второе уравнение: 9х = 6у.
Так
как х и ув обоих уравнениях обозначают одни и те же величины,
можно составить систему уравнений: 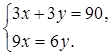
Решаем систему уравнений.
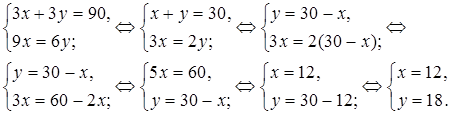
Итак, решение системы: (12; 18). Значит, 1 м первой ткани стоит 12 рублей, а 1 м второй – 18 рублей.
О т в е т: 12 р., 18 р.
Задача № 8
Р е ш е н и е.
Пусть в первом корпусе было х мест, а во втором у мест. Так как по условию задачи в обоих корпусах вместе было 720 мест, то можно составить уравнение: х + у = 720.
Поскольку число мест в первом корпусе увеличилось на 15 %, то есть на 0,15х мест, а во втором – на 10 %, то есть на 0,1у мест, причем общее число мест в обоих корпусах увеличилось на 80, то можно составить второе уравнение: 0,15х + 0,1у = 80.
Итак,
имеем систему уравнений: 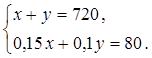
Решаем полученную систему уравнений:
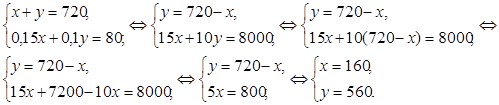
Значит, в первом корпусе первоначально было 160 мест, затем стало: 160 · 1,15 = 184; во втором корпусе первоначально было 560 мест, затем стало: 560 · 1,1 = 616 мест.
О т в е т: 184 места и 616 мест.
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача № 1
По шоссе движутся две автомашины с одной и той же скоростью. Если первая машин увеличит свою скорость на 10 км/ч, а вторая – уменьшит на 10 км/ч, то первая автомашина за 5 часов пройдет столько же, сколько вторая за 7 часов. С какой скоростью движутся автомашины?
Задача № 2
Два токаря должны изготовить по 40 деталей. Сколько деталей в час изготавливал первый токарь, если второй, изготавливая на 3 детали в час меньше, затратил на всю работу на 3 часа больше?
Задача № 3
Группа школьников купила мороженое, уплатив за покупку 1 р. 45 к. монетами достоинством в 10 к. и 15 к. Сколько монет по 10 к. и сколько монет по 15 к. отдали школьники за покупку, если всего было отдано 11 монет?
Задача № 1
О т в е т: 60 км/ч.
Задача № 2
О т в е т: 8 деталей в час.
Задача № 3
О т в е т: 4 монеты по 10 к. и 7 монет по 15 к.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.