Задания № 24 для подготовки к ОГЭ

Исследование по заданию 24 (ОГЭ 2020)

1. Отрезки AB и DC лежат на па­рал­лель­ных прямых, а от­рез­ки AC и BD пе­ре­се­ка­ют­ся в точке M. Най­ди­те MC, если AB = 13, DC = 65, AC = 42.

Решение:
1)Углы DCM и BAM равны как накрест лежащие при параллельных прямых

2)углы DMC и BMA равны как вертикальные, следовательно, треугольники DMC и BMA подобны по двум углам.

Значит,  

Следовательно, AM=0,2

Тогда AC=AM+MC=0,2MC+MC=1,2MC, а значит, MC== 35

Ответ: 35.

Подобные задачи:

·         Отрезки AB и DC лежат на па­рал­лель­ных прямых, а от­рез­ки AC и BD пе­ре­се­ка­ют­ся в точке M. Най­ди­те MC, если AB = 14, DC = 56, AC = 40 .(Ответ: 32)

·         От­рез­ки AB и DC лежат на па­рал­лель­ных пря­мых, а от­рез­ки AC и BD пе­ре­се­ка­ют­ся в точке M. Най­ди­те MC, если AB = 11, DC = 55, AC = 30. ( Ответ: 25)

·         Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и  BD пересекаются в точке M. Найдите MC, если AB = 10, DC = 25, AC = 56.( Ответ: 40)

·         Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и  BD пересекаются в точке M. Найдите MC, если AB = 11, DC = 22, AC = 27. (Ответ: 18)

2. Окруж­ность с цен­тром на сто­ро­не AC тре­уголь­ни­ка ABC про­хо­дит через вер­ши­ну C и ка­са­ет­ся пря­мой AB в точке B. Най­ди­те AC, если диа­метр окруж­но­сти равен 3, 6, а AB = 8.

Решение:

Пусть О — центр окружности. Радиус окружности, проведённый в точку касания, перпендикулярен касательной. Поэтому треугольник OBA — прямоугольный. Найдём OA по теореме Пифагора:

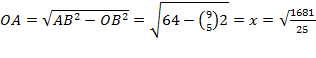 = = 8,2

Следовательно, длина стороны AC равна AC=CO+ OA=1,8+8,2= 10

Ответ: 10

Подобные задачи:

·         Окружность с цен­тром на сто­ро­не AC тре­уголь­ни­ка ABC про­хо­дит через вер­ши­ну C и ка­са­ет­ся пря­мой AB в точке B. Най­ди­те AC, если диа­метр окруж­но­сти равен 7,5, а AB = 2. (Ответ: 8)

·         Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8, а AB = 3 (Ответ: 9)

·         Окруж­ность с цен­тром на сто­ро­не AC тре­уголь­ни­ка ABC про­хо­дит через вер­ши­ну C и ка­са­ет­ся пря­мой AB в точке B. Най­ди­те AC, если диа­метр окруж­но­сти равен 8,4, а AB = 4. (Ответ: 10)

·         Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 16, а AB = 15. (Ответ: 25)

    3.В вы­пук­лом четырёхугольнике NPQM диа­го­наль NQ яв­ля­ет­ся бис­сек­три­сой угла PNM и пе­ре­се­ка­ет­ся с диа­го­на­лью PM  в точке S. Най­ди­те NS, если известно, что около четырёхугольника NPQM можно опи­сать окружность, PQ = 55, SQ = 1.

    Решение:

Углы Q NM и QPM — вписанные, опираются на одну и ту же дугу, следовательно, они равны. Рассмотрим треугольники  и  углы  и  равны, угол  — общий, следовательно, эти треугольники подобны. Откуда получаем:

 =

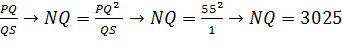
Таким образом, NS=NQ-QS=3025-1=3024

Ответ: 3024

Подобные задачи:

·         В вы­пук­лом четырёхугольнике NPQM диа­го­наль NQ яв­ля­ет­ся бис­сек­три­сой угла PNM и пе­ре­се­ка­ет­ся с диа­го­на­лью PM в точке S. Най­ди­те NS, если известно, что около четырёхугольника NPQM можно опи­сать окружность, PQ = 86, SQ = 43.(Ответ: 129)

      4.Основания рав­но­бед­рен­ной тра­пе­ции равны 8 и 18, а её пе­ри­метр равен 52. Най­ди­те пло­щадь трапеции.

Решение:

Рас­смот­рим рав­но­бед­рен­ную тра­пе­цию  ABCD  с ос­но­ва­ни­я­ми  BC=8  и  AD=18, пе­ри­метр ко­то­рой равен 52. Имеем AB=CD= 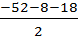=13

Пусть BH — вы­со­та тра­пе­ции. Тогда AH= 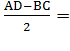 5. Из пря­мо­уголь­но­го треугольника ABH находим BH==12.

Значит, площадь трапеции равна BH= 156

Ответ: 156

Подобные задачи:

·         Основания рав­но­бед­рен­ной тра­пе­ции равны 8 и 18, а её пе­ри­метр равен 56. Най­ди­те пло­щадь трапеции. (Ответ: 130)

·