Задания для самостоятельной работы ученика

       Цели урока:

1.      Сформировать у учащихся понятие арифметической прогрессии и научить применять формулы к решению практических задач.

2.      Закрепление понятий прогрессия, член прогрессии, разность, прогрессии, сумма.  

3.   Отработать  умения  и навыки  применения формул n-го члена прогрессии,    суммы n - первых членов, свойств членов прогрессии.

       Задачи:

·         развивать умения и навыки применять формулы прогрессий при решении задач;

·         повысить интерес к предмету, расширить кругозор по данной теме.

Тип урока:  урок закрепления материала.

Оборудование урока ИД, презентация.

Ход урока

1.      Организационный момент.

2.      Самоопределение к деятельности

«Числа управляют миром»,- говорили древнегреческие ученые.  «Все есть число». Согласно их философскому мировоззрению, числа управляют не только мерой и весом, но также явлениями,  происходящими в природе,  и являются сущностью гармонии, царствующей в мире, душой космоса. Так первым четырем числам – 1, 2, 3, 4 – приписывалось: 1 – означает огонь, 2 – землю, 3 – воду, 4 – воздух. Сумма этих чисел – число 10 – изображало весь мир.

Но числа дают возможность самому человеку управлять миром. Сегодня на уроке мы продолжим работать с числами.

Для ввода в тему и мотивации учащихся используется следующая задача:

      Улитка ползёт по дереву. За первую минуту она проползла 30см, а за каждую следующую минуту – на 5см больше, чем за предыдущую. За какое время достигнет улитка вершины дерева длиной 5,25м, если считать, что движение начато от его основания? 

Вопрос. О каком математическом понятии идет речь в данной задаче?

3.Постановка цели урока.

Продолжить работу над определениями:

1.  арифметической прогрессии

2. разности арифметической прогрессии

Совершенствовать навыки применения формул арифметической прогрессии

1.  формулы n-го члена

2. формулы суммы n первых членов;

4. Актуализация знаний и умений учащихся

1. Что мы уже знаем об арифметической прогрессии?

·         Определение арифметической прогрессии

·         определение разности

·         формула n-го члена арифметической  прогрессии

·         свойство n-го члена арифметической  прогрессии

Вывод:

            Зная эти формулы, можно решать много интересных задач литературного, исторического и практического содержания.

5. Устная работа

v  «Проверь себя!»

Какие из последовательностей являются арифметическими прогрессиями?

3, 6, 9, 12,…..           (d=3)                

5, 12, 18, 24, 30,….. (нет)

7, 14, 28, 35, 49,…. (нет)

5, 15, 25,….,95…. (d=10)                

1000, 1001, 1002, 1003,….  (d=1)                

1, 2, 4, 7, 9, 11…..  (нет)

5, 4, 3, 2, 1, 0, -1, -2,…. (d= - 1)                

v  «Вычисли устно»

Найти разность арифметической прогрессии:

1; 5; 9………

105; 100….

-13; -15; -17……

11; ? ; 19,….

6. Самостоятельная работа

Проверим, что  мы  уже умеем  делать

Условия задач связаны между собой по принципу эстафеты.

Ответы: 1) d = 0,5; 2) a₇ = -1; 3) a₁ = 13; 4) n = 71.

7. Выполнение упражнений

Обращаемся к страницам истории.

“Пусть властно по своей орбите нас ритм сегодняшний кружит –
Вернее будущее видит лишь тот, кто прошлым дорожит”

На этом этапе происходит расширение знаний и умений учащихся через интеграцию с историей.

1.       Египетские страницы

Папирус Ахмеса.(2000 до н.э.) В записях встречается формула .

Что она может означать? И пользуемся мы такой формулой сегодня?

Решение предложенное учениками:

; ; ;

Сегодня, используя эту формулу, мы находим сумму первых n членов арифметической прогрессии Оказывается, что 4 тыс. лет назад древние египтяне решали те же задачи, что и мы.

2.       Вавилонские страницы.

Исследование клинописных текстов эпохи Хаммурапи (XVIII в до н. э.) открыло для нас задачи на прогрессию.

“10 братьев делят 100 шекелей серебра; брат над братом поднимается, на сколько поднимается я не знаю. Доля восьмого – шесть шекелей. Брат над братом на сколько поднимается?”

Решение: n = 10, S_n = 100, a₈ = 6. Найти d. Ответ: на 1,6 шекелей

3.      Европейские страницы.

Здесь мы преследуем цель познакомиться с ещё одним из известных математиков.

Об одном интересном эпизоде из жизни немецкого математика К.Ф.Гаусса (1777-1855).

Когда ему было 9 лет, учитель, стремясь надолго занять детей, задал на уроке следующую задачу.

“Сосчитать сумму всех натуральных чисел от 1 до 40”

На удивление учителя один из учеников (это был Гаусс) через минуту воскликнул: “Я уже решил”. В тетради Гаусса было только одно число, но зато верное.

Ребятам предлагается решить туже самую задачу, ведь 9 – летний Гаусс с ней справился. Рассуждения Гаусса – как проверка.

8.     «Психологическая разгрузка».

У Вас на столах лежат листы, на которых написаны цифры от 1 до 9. Теперь раскрасьте один ряд двумя разными цветами в любом порядке. Как я это сделала, показано на слайде.

А пока Вы раскрашиваете, я расскажу про замечательного математика по фамилии Рамсей. Он жил в начале ХХ века. Им была создана теория, доказывающая, что в мире нет абсолютного хаоса. Что даже, казалось бы, самая неупорядоченная система имеет определенные математические закономерности. Вспомните, когда Вы смотрите на звезды, то может показаться, что расположены они в самом случайном порядке. Но еще в древности люди увидели там созвездия Рыб и Касеопеи, Льва и Ориона.

И вот на ваших карточках казалось бы цифры раскрашены в случайном порядке. Но Рамсей доказал, что это не так, доказав следующий факт: Обратите внимание, что хотя бы три каких – либо числа одного цвета обязательно составляют арифметическую прогрессии. Запишите эти числа.

9.Работа в группах

«Прогрессии в жизни и быту»

1 группа.

№1.

Штангист поднимает штангу весом 45кг.С каждым подходом вес штанги увеличивается на 5 кг. Сколько кг поднимет штангист за 7 подходов?

Дано: арифметическая прогрессия ,а₁=45,d=5 ,n=7

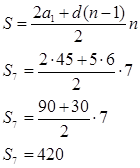Найти: S

Решение

 Ответ: за 7 подходов штангист поднимет 420кг

 2. группа

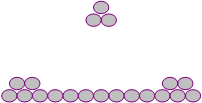
При хранении бревен строевого леса их укладывают так, как показано на рисунке.

Сколько бревен находится в одной кладке, если в ее основание положить 12 бревен?

Решение:

 a₁=1, a₁₂= 12, S₁₂-?

S₁₂ = (a₁+a₁₂)/2*12=(1+12)*6=78

Ответ: 78 бревен

 3 группа  «Наследство».

Джентльмен получил наследство. Первый месяц он истратил 1000$, а каждый следующий месяц он тратил на 500$ больше, чем в предыдущий. Сколько $ он истратил за второй месяц? За третий? Каков размер наследства, если денег хватило на год такой безбедной жизни?

Решение:

Применив формулу , получаем:

Применив формулу: , получим:

 4.  группа

Рабочий выложил плитку следующим образом: в первом ряду - 3 плитки, во втором - 5 плиток и т.д., увеличивая каждый ряд на 2 плитки. Сколько плиток понадобиться для 7 ряда?

Решение:

a₁=3, d=2,  a₇ -?

a₇=a₁+6*d=3+2*6=15

9. Задачи на арифметическую прогрессию, встречающиеся в ГИА и ЕГЭ

В задачах встречающихся на ЕГЭ

1.      Автотурист на автомобиле  в первый день проехал 720 км. В каждый следующий он проезжает на 40 км меньше. Сколько дней путешествовал автотурист, если за всё время путешествия  он проехал 5040 км?

2.      В стране 10 аэропортов. С самого крупного за сутки взлетает 42 самолёта, а с каждого последующего ( в порядке убывания интенсивности) на 4 меньше. Сколько самолётов взлетает в сутки со всех 10 аэропортов?

Задачи встречающиеся в ГИА.

1.      Арифметическая прогрессия задана формулой а_n=4n -4.  Какое из следующих чисел является членом этой прогрессии?

    А) 34             Б) 27            В) 72             Г) 10

2.      Арифметическая прогрессия задана условиями а₁=6, а_п+1=а_п +6. Какое из данных чисел является членом этой прогрессии?

А) 18             Б) 56            В) 48             Г) 32

3.      Арифметическая прогрессия задана условиями а₁=3, а_п+1=а_п – 2,5. Найдите а₄?

4.      Дана арифметическая прогрессия.  а₄=3, а₉= – 17. Найдите разность этой прогрессии?

5.       Дана арифметическая прогрессия: ,  2,    , … Найдите сумму первых шести её членов.

6.      Между числами 6 и 17 вставьте четыре числа так, чтобы вместе с данными числами они образовали арифметическую прогрессию.

7.      Между числами 12 и 26 вставьте три числа так, чтобы вместе с данными числами они образовали арифметическую прогрессию.

8.       В арифметической прогрессии а₅=10, а₁₁= 40. Найдите а₈ -?

9.      Найдите сумму всех чётных натуральных чисел от 20 до 200 включительно.

Домашнее задание:

п. 16, № 16.43, № 16.45, № 16.47

Дополнительная задача:

1.      Каждый курильщик выкуривает в день в среднем 8 сигарет. После выкуривания первой сигареты   в легких оседает 0,0002 г никотина и табачного дёгтя. С каждой последующей сигаретой это количество вредных веществ увеличивается на 0,000001 г. Какое количество никотина и дёгтя оседает в лёгких за год?

10.Рефлексия.  Подведение  итогов.

И вспомним начало нашего урока, ребята.

Удалось ли за сегодняшний урок сделать чудные открытия?

Как Вы считаете, нам удалось достигнуть поставленных целей?

Ян Амос Коменский говорил: «Считай  несчастным  тот  день  или тот  час,  в  который  ты  не  усвоил ничего  нового,  ничего  не  прибавил  к своему образованию». Я надеюсь, что в сегодняшнем уроке вы найдете для себя хоть крупинку полезного.

Учитель: У каждого из вас на столе карточки (розовая, зелёная, жёлтая). Уходя из класса, прикрепите на доску одну из них.

Карточка розового цвета обозначает: “Я удовлетворён уроком, урок был полезен для меня, я много, с пользой и хорошо работал на уроке, и получил заслуженную оценку, я понимал всё, о чём говорилось и что делалось на уроке”.

Карточка зеленого цвета обозначает: “Урок был интересен, я принимал в нём активное участие, урок был в определённой степени полезен для меня, я отвечал с места, я сумел выполнить ряд заданий, мне было на уроке достаточно комфортно”.

Карточка желтого цвета обозначает: “Пользы от урока я получил мало, я не очень понимал, о чём идёт речь, мне это не очень нужно, домашнее задание я не понял, к ответу на уроке я был не готов”.