Задания по математике на нахождение площади, 2 класс

Урок 64
Площадь фигуры. Единицы площади

Цели урока: ввести термин «площадь фигуры»; познакомить учащихся с единицами площади (квадратным метром, квадратным дециметром, квадратным сантиметром) и их обозначениями; закреплять табличные случаи умножения и деления на 2, 3, 4, 5, 6; совершенствовать навыки вычисления доли числа; развивать умения анализировать и обобщать.

Ход урока

I. Организационный момент.

II. Устный счет.

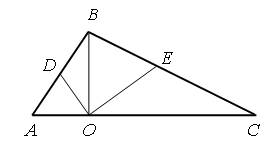
1. Сколько треугольников вы видите на чертеже?

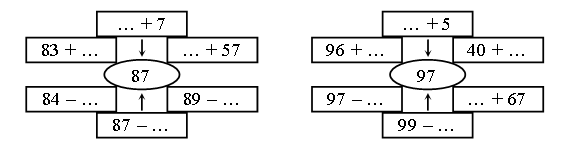
2. Вставьте пропущенные числа.

3. Задачи.

а) В столовом сервизе 12 глубоких и столько же мелких тарелок. Сколько тарелок в этом сервизе?

б) Уже прошло 30 минут урока. Через 5 минут прозвенит звонок. Сколько минут продолжается урок в нашей школе?

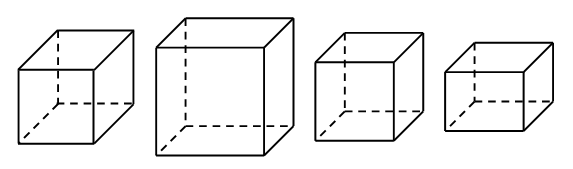
4. Заштрихуйте передние грани кубов, изображенных верно.

III. Сообщение темы урока.

– Как называются данные на доске фигуры?

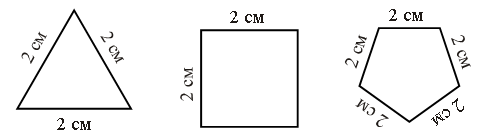
– Что их объединяет? (Это многоугольники, стороны которых равны 2 см.)

– Как найти периметр каждого многоугольника?

 = 2 · 3 = 6 (см)  или  2 + 2 + 2 = 6 (см).

  = 2 · 4 = 8 (см)  или  2 + 2 +2 + 2 = 8 (см).

  = 2 · 5 = 10 (см)  или  2 + 2 + 2 + 2 + 2 = 10 (см).

– Как найти площадь этих фигур?

– Какие трудности у вас возникли?

– Сегодня на уроке мы узнаем, что называют площадью фигуры.

IV. Изучение нового материала.

Задание № 1 (с. 22).

– Мастер облицовывает плитками в ванной комнате две стены. Каждая плитка квадратной формы с длиной стороны 1 дм. Ее площадь считают равной одному квадратному дециметру. Записывают так: 1 дм².

– Рассмотрите таблицу в учебнике.

– Сколько плиток пошло на облицовку одной стены? (12.)

– Другой стены? (15.)

– На какую стену мастер израсходовал больше плиток?

– Назовите площадь каждой стены в квадратных дециметрах. (12 дм² и 15 дм².)

– Площадь какой стены больше и почему?

– Прочитайте определение квадратного дециметра на с. 22 учебника.

– Сформулируйте определение квадратного сантиметра. (Квадратным сантиметром называют площадь квадрата с длиной стороны 1 см.)

– Сформулируйте определение квадратного метра.

– Квадратный сантиметр, квадратный дециметр, квадратный метр – это единицы площади.

Их обозначают так: см², дм², м².

– Покажите вырезанные из бумаги квадраты площадью 1 дм², 1 см² и 1 м².

– Сравните попарно площади этих квадратов, накладывая меньший квадрат на больший.

– В квадрате площадью 1 дм² может уместиться ровно 100 квадратов площадью 1 см², а в квадрате площадью 1 м² – ровно 100 квадратов площадью 1 дм².

Справочный материал для учителя

Фигура на рисунке 1 состоит из 8 квадратов со стороной 1 см каждый. Площадь одного такого квадрата называют квадратным сантиметром. Пишут: 1 см². Значит, площадь всей фигуры равна 8 см².

Если какую-нибудь фигуру можно разбить на р квадратов со стороной 1 см, то ее площадь равна р см².

Прямоугольник на рисунке 2 состоит из 3 полос, каждая из которых разбита на 5 квадратов со стороной 1 см. Весь прямоугольник состоит из 5 · 3 = 15 таких квадратов, и его площадь равна 15 см².

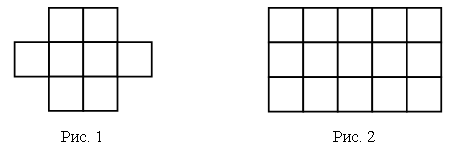
Чтобы найти площадь прямоугольника, надо умножить его длину на ширину.

Запишем это правило в виде формулы. Площадь прямоугольника обозначим буквой S, его длину – буквой а, а ширину – буквой b.

Получаем формулу площади прямоугольника:

  

Две фигуры называют равными, если одну из них можно так наложить на вторую, что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Линия KLMN на рисунке 3 разбивает прямоугольник ABCD на две части. Одна из частей имеет площадь 12 см², а другая – 9 см². Площадь всего прямоугольника равна 3 · 7, то есть 21 см². При этом 21 = 12 + 9.

Площадь всей фигуры равна сумме площадей ее частей.

Отрезок АС разбивает прямоугольник на два равных треугольника: ABC и ADC (рис. 4).

Площадь каждого треугольника равна половине площади всего прямоугольника.

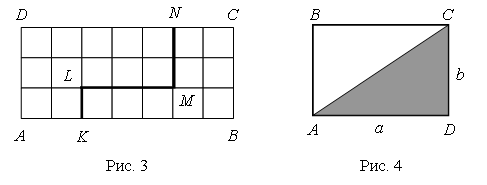
· Квадратной единицей называют не квадрат, а его площадь.

· Квадратным сантиметром называют площадь квадрата с длиной стороны 1 см.

· Квадратным дециметром называют площадь квадрата с длиной стороны 1 дм.

· Квадратным метром называют площадь квадрата с длиной стороны 1 м.

! Следите за правильным применением учащимися терминологии. В быту дети довольно часто слышат, как взрослые говорят о том, что площадь такой-то комнаты или квартиры равна 15 м, 60 м и т. д. Разъясните, что в этих случаях речь идет о площадях 15 м², 60 м², а не о длинах.

– Рассмотрите рисунок на с. 23 учебника и объясните, как найти площадь фигуры. (Надо разделить фигуры на квадраты с длиной стороны 1 см и пересчитать, сколько получилось квадратов.)

Задание № 2 (с. 23).

Учащиеся читают величины, записанные единицами площади.

Задание № 3 (с. 23).

Выполняя задание, учащиеся устанавливают взаимосвязь между двумя изученными единицами площади: 1 дм² = 100 см².

Не следует требовать от учащихся знания наизусть этой зависимости.

Задание № 4 (с. 23).

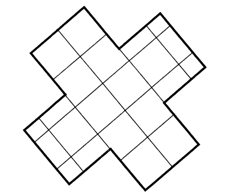
Для выполнения задания учащиеся используют палетку. Цель задания – научить детей измерять площадь фигур с помощью палетки. Сначала объясните ученикам, как надо накладывать палетку на фигуру, чтобы было удобно выполнять измерения, и только потом переходите к практической работе. Рассуждать дети должны примерно так: «В голубой фигуре ровно 13 квадратов. Площадь каждого квадрата – 1 см², значит, площадь фигуры – 13 см².

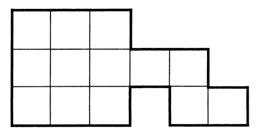
В желтой фигуре ровно 12 квадратов (их площадь – 12 см²), 6 половинок квадратов (их площадь – 3 см²) и 4 четвертинки квадрата (их площадь – 1 см²). Следовательно, площадь желтой фигуры:

12 + 3 + 1 = 16, то есть 16 см²».

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 11 (с. 25).

Вывод: чтобы найти неизвестный делитель, надо делимое разделить на значение частного.

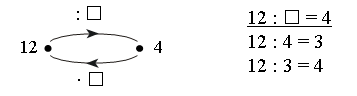
Задание № 13 (с. 25).

Ответ: пятая часть, четвертая часть и две шестых части.

2. Работа в печатной тетради № 2.

Задание № 35.

Чертеж:

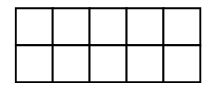
Ответ: 10 см².

Задание № 192.

Ответ: 7 см² и 8 см².

VI. Итог урока.

– Что нового узнали на уроке?

– Назовите единицы измерения площади фигуры.

Домашнее задание: № 10, 12 (учебник); № 32, 191 (рабочая тетрадь).

 

 

 

 

 

 

 

 

 

 

Урок 65
Площадь фигуры. Единицы площади

Цели урока: продолжить формирование умений определять площадь фигуры приемом пересчитывания квадратов, на которые разделена фигура; совершенствовать навыки работы с математическими графами; развивать логическое мышление и умение рассуждать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Вставьте пропущенные числа.

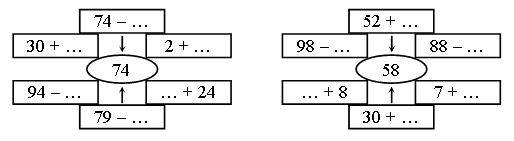
2. Задача.

Почтальон принес в наш дом 2 десятка газет и 8 журналов – в каждую квартиру что-нибудь одно. Сколько квартир получили газету или журнал?

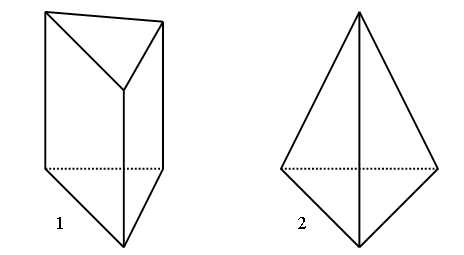
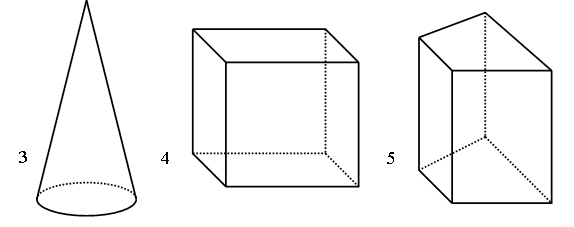
3. Рассмотрите чертеж:

а) Какая фигура «лишняя»?

б) У какой фигуры 6 вершин, 5 граней, 9 ребер?

в) У какой фигуры только одна вершина?

г) В чем сходство и различие фигур 4 и 5?

д) Названия каких из этих фигур ты знаешь?

III. Сообщение темы урока.

– Сегодня на уроке будем определять площадь различных геометрических фигур.

IV. Изучение нового материала.

Задание № 5 (с. 24).

Предложите учащимся выполнить чертеж клумб не в тетради, а на отдельном листе бумаги. Это позволит легко организовать самостоятельную проверку. Для этого дети вырезают ножницами изображения клумб и накладывают их друг на друга. Если четырехугольная «клумба» полностью уместится на треугольной, то задание выполнено верно.

Задание № 6 (с. 24).

Чертежи:

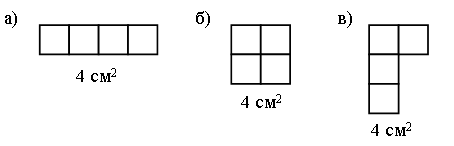
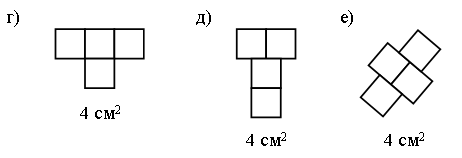
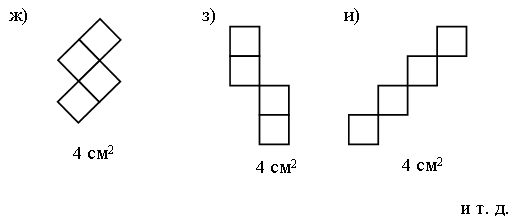
Задание № 7 (с. 24).

– Прочитайте текст. Является ли он задачей? Почему?

– Что известно? Что надо узнать?

– Запишите кратко условие задачи и решите ее.

Решение:

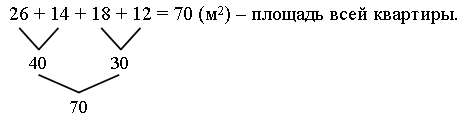
Ответ: 70 м².

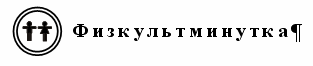
V. Повторение пройденного материала.

1. Работа в печатной тетради № 2.

Задание № 34.

Площадь фигуры № 1 – 6 см².

Площадь фигуры № 2 – 8 см².

Площадь фигуры № 3 – 7 см².

Сложнее всего найти площадь фигуры № 4. Учащиеся должны рассуждать примерно так: «В синей фигуре 10 квадратов (их площадь – 10 см²) и 4 половинки (их площадь – 2 см²). Следовательно, площадь красной фигуры:

10 + 2 = 12, то есть 12 см²».

Площадь фигуры № 5 – 20 см².

Площадь фигуры № 6 – 32 см².

2. Работа по учебнику.

Задание № 16 (с. 26).

· Пять больше трех.

· Двадцать шесть больше трех.

· Двадцать шесть больше пяти.

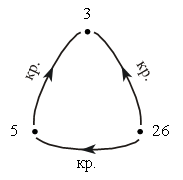
– Какое отношение задает первый граф? (Отношение «больше».)

– Какое отношение задает второй граф? (Отношение «меньше».)

· 20 меньше 70.

· 15 меньше 70.

· 15 меньше 20.

· 15 меньше 81.

· 20 меньше 81.

· 70 меньше 81.

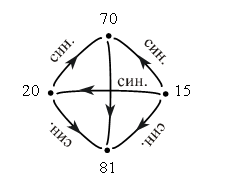
Задание № 17 (с. 26).

– Прочитайте текст. Является ли он задачей? Почему?

– Что известно? Что требуется узнать?

– Запишите кратко условие задачи и решите ее.

Запись:

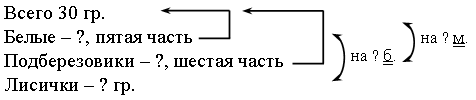
Решение:

1. Сколько белых грибов принес Миша?

 30 : 5 = 6 (гр.)

2. Сколько подберезовиков принес?

 30 : 6 = 5 (гр.)

3. Сколько принес лисичек?

 20 – 5 – 6 = 9 (гр.)

4. На сколько больше нашел лисичек, чем белых грибов?

 9 – 6 = 3 (гр.)

5. На сколько меньше нашел подберезовиков, чем белых грибов?

 6 – 5 = 1 (гр.)

VI. Итог урока.

– Что нового узнали на уроке?

– Какие правила математических граф вам известны?

Домашнее задание: № 14, 15 (учебник); № 195 (рабочая тетрадь).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок 66
Площадь фигуры. Единицы площади

Цели урока: совершенствовать навыки определения площади фигуры; закреплять умение решать задачи с величинами «цена», «количество», «стоимость»; развивать внимание и логическое мышление.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Разгадайте правило, по которому записан каждый ряд чисел и продолжите его.

19, 17, 15, …

71, 73, 75, …

44, 46, 45, 47, 46, …

23, 26, 24, 27, …

91, 95, 92, 96, 93, …

2. Задача.

Аудиокассета рассчитана на 60 минут записи. На этой кассете у меня уже записана музыка, звучащая 56 минут. Уместится ли на кассете еще одна песня, запись которой занимает 4 минуты?

3. Рассмотрите чертеж.

Выберите фигуру, которую нужно нарисовать.

 

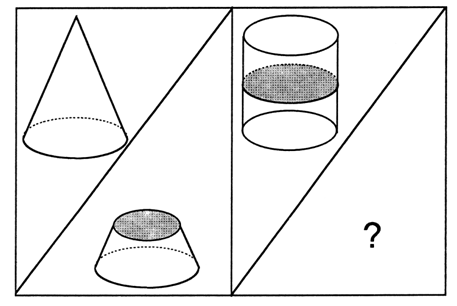
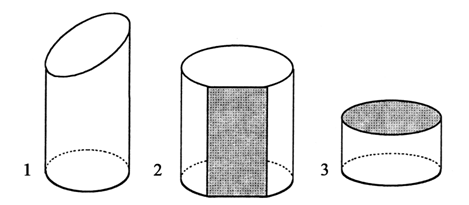
III. Сообщение темы урока.

– Прочитайте величины, записанные на доске.

– Зачеркните «лишнюю» величину в каждой строке:

а) 91 см, 10 дм, 100 м, 29 см², 41 дм;

б) 45 кг, 24 дм², 83 см², 15 дм², 43 м²;

в) 25 м², 68 м², 38 см², 74 м², 91 см².

– Сегодня на уроке будем определять площадь различных многоугольников.

IV. Изучение нового материала.

Задание № 8 (с. 24).

– Прочитайте задание.

– Какую форму должен иметь кусок ткани? (Форму квадрата.)

– Какой длины должны быть стороны квадрата? (По 6 см.)

– Какой вывод вы можете сделать? (Для заплатки потребуется кусок ткани квадратной формы со сторонами по 6 см.)

– Изобразите такую заплатку в тетради.

– Найдите площадь заплатки.

Решение:  6 + 6 + 6 + 6 + 6 + 6 = 36 (см²).

Задание № 9 (с. 24).

– Чему равна площадь квадратной обертки? (25 см².)

– Что вы можете сказать о квадрате? (У квадрата все стороны равны.)

– Чему равна длина сторон этой обертки? (5 см².)

– Сделайте проверку. Постройте в тетради квадрат с длинами сторон по 5 см и убедитесь, что его площадь равна 25 см².

Работа по карточкам.

Закрасьте:  20 см² – синим цветом;

     5 см² – красным цветом;

     30 см² – зеленым цветом.

– Какая площадь 1 дм² осталась незакрашенной?       

Учащиеся работают самостоятельно.

Работы сдаются учителю на проверку.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 18 (с. 26).

– Прочитайте текст. Является ли он задачей? Почему?

– Что известно? Что требуется узнать?

– Запишите кратко условие задачи и решите ее.

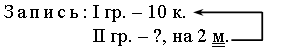
     Разложили – в 6 с. по ? к.

Решение: 1) 10 – 2 = 8 (к.) – со II грядки.

  2) 10 + 8 = 18 (к.) – всего.

  3) 18 : 6 = 3 (к.) – в каждой сетке.

Ответ: 3 к.

Задание № 20 (с. 26).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Запишите условие задачи в таблицу.

Решение: 1) 3 · 4 = 12 (р.) – стоимость сырков.

   2) 12 + 28 = 40 (р.) – стоимость всей покупки.

Ответ: 40 рублей.

Задание № 22 (с. 27).

– Рассмотрите рисунок и составьте по нему задачу.

Задача. В мотке было 30 м. Отрезали 12 м 50 см. Какой длины канат остался в мотке?

– Можно ли сразу ответить на вопрос задачи?

– Запишите кратко условие задачи.

Запись: Было – 30 м.

   Отрезали – 12 м 50 см.

   Осталось – ?

Решение:

30 м – 12 м 50 см = 17 м 50 см

Ответ: 17 м 50 см.

2. Работа в печатной тетради № 2.

Задания № 36, 37, 38.

Эти задания являются подготовительными для введения отношений «больше в...» и «меньше в...».

VI. Итог урока.

– Что нового узнали на уроке?

– Что называют площадью фигуры?

– Назовите единицы площади.

Домашнее задание: № 19 (учебник); № 39, 40 (рабочая тетрадь).

 

 

 

 

 

Урок 67
Практическая работа по теме
«Площадь фигуры. Единицы площади»

Цели урока: проверить умения и навыки вычисления площади фигуры; развивать практические навыки, внимание и умение анализировать.

Ход урока

I. Организационный момент.

II. Практическая работа.

Задание № 1.

Дорисуйте фигуру так, чтобы получился прямоугольник, площадь которого равна:

       а) 9 см²,                                                  б) 21 см²,

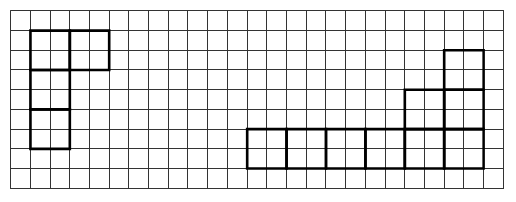
        в) 15 см²,                                                г) 18 см²,

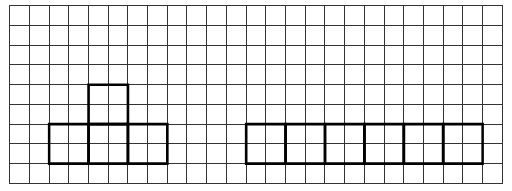
       д) 27 см².

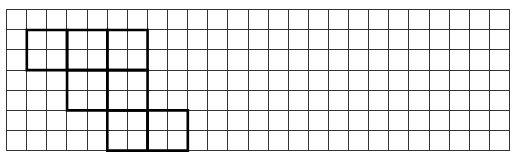
Задание № 2.

Вычислите периметр и площадь фигуры удобным способом.

Задание № 3.

Разделите фигуру на многоугольники площадью 4 см². Если сможете, найдите несколько решений.

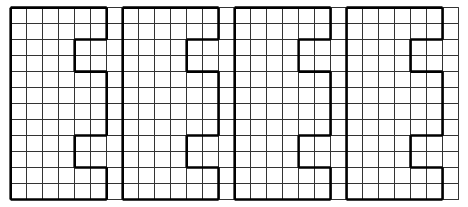
Чему равны у этой фигуры площадь

 

и периметр

?

 

 Выберите любое из ваших решений и составьте из полученных четырех многоугольников другую фигуру, не выходящую за границу прямоугольника:

Чему равны у этой фигуры площадь

 

и периметр

?

III. Итог урока