


 Многие ученые вплоть
до начала XVII в. считали, что движение небесных тел должно быть равномерным и
происходить по «самой совершенной» кривой – окружности.
Многие ученые вплоть
до начала XVII в. считали, что движение небесных тел должно быть равномерным и
происходить по «самой совершенной» кривой – окружности.
Кеплеру удалось преодолеть этот предрассудок и установить действительную форму планетных орбит, а также закономерность изменения скорости движения планет при их обращении вокруг Солнца.
В своих поисках Кеплер исходил из убеждения, что «в мире правит число», высказанного еще Пифагором. Он искал соотношения между различными величинами, характеризующими движение планет, — размеры орбит, период обращения, скорость.
Кеплер действовал фактически вслепую, чисто эмпирически.
При построении орбиты Марса Кеплер воспользовался собственными наблюдениями планеты, а также многолетними определениями координат и конфигураций Марса, проведёнными его учителем Тихо Браге.

Тихо Браге
 Орбиту Земли Кеплер
считал (в первом приближении) окружностью, что не противоречило наблюдениям.
Орбиту Земли Кеплер
считал (в первом приближении) окружностью, что не противоречило наблюдениям.
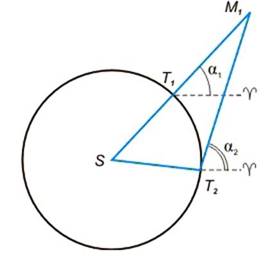
Построение
орбиты Марса Кеплером
Пусть нам известно угловое расстояние Марса от точки весеннего равноденствия во время одного из противостояний планеты (α1), где Т1 и М1 – положения Земли и Марса на орбите.
Спустя 687 суток (звездный период обращения Марса) планета придет в ту же точку своей орбиты. Земля в этот момент находится в точке Т2, и, следовательно, угол α2 есть прямое восхождение Марса.
Повторив подобные операции для нескольких других противостояний Марса, Кеплер получил еще целый ряд точек и, проведя по ним плавную кривую, построил орбиту планеты.
Орбиту Земли Кеплер считал (в первом приближении) окружностью, что не противоречило наблюдениям.
 В ходе построения
орбиты планеты Марс Кеплер был поставлен перед необходимостью сделать выбор
одного из двух возможных решений:
В ходе построения
орбиты планеты Марс Кеплер был поставлен перед необходимостью сделать выбор
одного из двух возможных решений:
1) считать, что орбита Марса представляет собой окружность, и допустить, что на некоторых участках орбиты вычисленные координаты планеты расходятся с наблюдениями (из-за ошибок наблюдений) на 8';
2) считать, что наблюдения таких ошибок не содержат, а орбита не является окружностью.
Будучи уверенным в точности наблюдений Тихо Браге, Кеплер выбрал второе решение.
Кеплер установил, что орбита Марса не окружность, а кривая, которая называется эллипсом, при этом Солнце не располагается в центре эллипса.

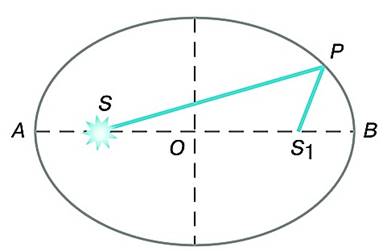 Эллипс – кривая, у которой сумма расстояний от любой точки до его
фокусов есть величина постоянная.
Эллипс – кривая, у которой сумма расстояний от любой точки до его
фокусов есть величина постоянная.
 Первый
закон Кеплера
Первый
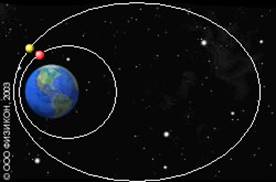
закон КеплераКаждая планета обращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.
Иллюстрация первого закона Кеплера на примере движения спутников Земли

Большая полуось характеризует размер орбиты планеты.
Перигелий – ближайшая к Солнцу точка орбиты.
Афелий – наиболее удалённая от Солнца точка орбиты.
 Второй
закон Кеплера
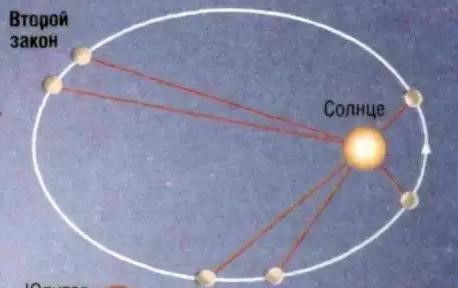
Второй
закон КеплераРадиус-вектор планеты за равные промежутки времени описывает равные площади.
Иллюстрация второго закона Кеплера на примере движения спутников Земли
 Согласно закону
сохранения энергии, полная механическая энергия замкнутой системы тел, между
которыми действуют силы тяготения, остается неизменной при любых движениях тел
этой системы. Поэтому сумма кинетической и потенциальной энергий планеты,
которая движется вокруг Солнца, неизменна во всех точках орбиты и равна полной
энергии.
Согласно закону
сохранения энергии, полная механическая энергия замкнутой системы тел, между
которыми действуют силы тяготения, остается неизменной при любых движениях тел
этой системы. Поэтому сумма кинетической и потенциальной энергий планеты,
которая движется вокруг Солнца, неизменна во всех точках орбиты и равна полной
энергии.
По мере приближения планеты к Солнцу возрастает ее скорость – увеличивается кинетическая энергия, но вследствие уменьшения расстояния до Солнца уменьшается энергия потенциальная.
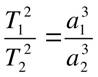 Третий
закон Кеплера
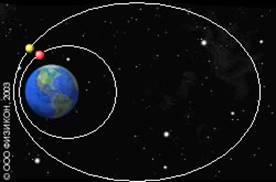
Третий
закон КеплераКвадраты звёздных периодов обращения планет относятся между собой как кубы больших полуосей их орбит.
Иллюстрация третьего закона Кеплера на примере движения спутников Земли
«То, что 16 лет тому назад я решил искать, <...> наконец найдено, и это открытие превзошло все мои самые смелые ожидания...»
Иоганн Кеплер
 Третий закон
позволяет вычислить относительные расстояния планет от Солнца, используя при
этом уже известные периоды их обращения вокруг Солнца.
Третий закон
позволяет вычислить относительные расстояния планет от Солнца, используя при
этом уже известные периоды их обращения вокруг Солнца.
Не нужно определять расстояние от Солнца каждой из них, достаточно измерить расстояние от Солнца хотя бы одной планеты.
Величина большой полуоси земной орбиты – астрономическая единица (а.е.) – стала основой для вычисления всех остальных расстояний в Солнечной системе.
Иоганн Кеплер
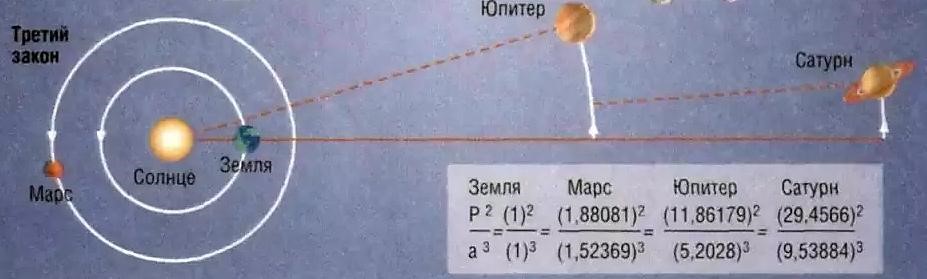
Задача. Противостояния некоторой планеты повторяются через два года. Чему равна большая полуось её орбиты?
 |
Находим большую полуось планеты:
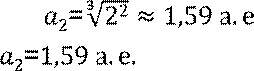 .
.
Ответ:
Вопросы (с. 62)
1. Сформулируйте законы Кеплера.
2. Как меняется скорость планеты при ее перемещении от афелия к перигелию?
3. В какой точке орбиты планета обладает
• максимальной кинетической энергией;
• максимальной потенциальной энергией?
Домашнее задание
1) § 12.
2) Упражнение 10.
1. Марс в 1,5 раза дальше от Солнца, чем Земля. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
2. Синодический период малой планеты 500 суток. Определите большую полуось ее орбиты и звездный период обращения.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.