Законы Кеплера.

Предмет: Астрономия.

Класс: 10 -11

Учитель: Елакова Галина Владимировна.

Место работы: Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №7» г Канаш Чувашской Республики                   

                   Тема: «Законы движения планет».

Цели: Организовать деятельность учащихся по изучению и первичному закреплению знаний учащихся по теме «Законы Кеплера», развивать способности к поиску решения проблемы, самостоятельному мышлению, умению формировать определения, стимулирование интереса к поиску фактов, событий; развитие коммуникативных способностей свободного и активного включения в диалог.

Оборудование: мультимедийный проектор, компьютер.

Планируемые результаты:

Предметные: выяснить, почему и как движутся планеты вокруг Солнца, размеры и массы, происхождение, столкновение с другими телами.

Основные понятия: деферент, большая полуось, малая полуось, перигелий, афелий, эксцентриситет эллипса, астрономическая единица, перигелий, афелий, апогей, перигей.

Метапредметные:

-коммуникативные: формирование компетентностей в использовании ИКТ, умение организовать учебное сотрудничество, работать в группе, участвовать в коллективном обсуждении проблем, уважительно относиться к позиции другого, пытаться договариваться; развивать навыки контроля и самоконтроля; совершенствовать умение вести предметный диалог.

- регулятивные: умение организовать свою учебную деятельность: определять цель работы, ставить задачи, планировать, соотносить свои действия с планируемыми результатами.

-познавательные: умение работать с разными источниками информации, умения анализировать, объяснять, доказывать, защищать свои идеи, определять причины явлений

Личностные результаты: развитие навыков сотрудничества со сверстниками, формирование уважительного отношения к иному мнению; формирование интеллектуальной, исследовательской, информационной культуры; развитие личностно-смыслового отношения к предметам; учиться взаимодействовать с другими, грамотно отстаивать свою точку зрения.

Межпредметные связи: астрономия, физика, литература, история.

Мотивация к учебной деятельности.

Цель: включение в учебную деятельность на личностно значимом уровне.

      Эпиграфом к нашему занятию будут следующие слова:

 «Знания бывают двух видов: мы сами знаем предмет, или же знаем, где найти о нем сведения». Бенджамин Франклин

                Вы узнаете:

- По каким законам движутся планеты.

- Как определить массы планет по элементам их движения.

- Как объяснялись видимые движения планет в системе мира Птолемея.

- В чем основное отличие Коперника от системы мира древних.

- Почему теория Коперника произвело переворот в мировоззрении.

- Как объяснил Коперник видимые петлеобразные движения планет.

- Какими представлял себе Коперник орбиты планет и как можно назвать систему   

   Коперника.

- Что такое эпицикл, деферент.

- Что такое эксцентриситет эллипса? Афелий? Перигелий? Перигей? Апогей?

               Вспомните:

- Что такое эллипс и каковы его основные элементы?

- Как формулируется закон всемирного тяготения?

- Что называется конфигурацией планеты?

- В чем различия геоцентрической и гелиоцентрической систем мира?

- Почему на звездных картах не указывают положение планет?

Попытаемся объяснить следующие вопросы:

  В чем сущность и значение открытия Коперника?

  Какое обоснование и развитие получили идеи гелиоцентризма в трудах Бруно, Галилея?

   В чем суть законов движения планет и как их обосновать?

  Почему большую полуось орбиты отождествляют с ее средним расстоянием от Солнца?

  На чем основывался Кеплер, открывая свои законы?

  В чем заключается обобщение Ньютоном законов Келера?

  Учитель: Поиск объяснения наблюдаемых движений планет изменил взгляд человека на мир. В «Альмагесте», написанном в 150 г. н. э., александрийский астроном Птолемей изложил древний геоцентрический 9т.е. ставящий Землю в центре Вселенной) взгляд на мир. Считалось, что орбиты имеют идеальные формы кругов. Предполагалось, что Солнце, Луна и пять планет движутся по малым кругам, называемым эпициклами, центры которых движутся вокруг Земли по большим кругам, называемым деферентами. В течение более чем четырнадцати столетий система Птолемея принималась в качестве основы для астрономических вычислений. Она с большей точностью описывала наблюдаемые положения и движения небесных тел и выражала общий, распространенный взгляд на мир, который сложился у людей при наблюдении неба. С небольшими изменениями геоцентрическая теория стала в средние века религиозной догмой.  

   Польский астроном Николай Коперник (1473 – 1543) подготовил труд, который увидел свет в год его смерти. В нем он изложил гелиоцентрическую систему, по которой в центре мира находится Солнце. В коперниканской системе планеты, включая Землю, обращаются вокруг неподвижного центрального Солнца. Согласно теории Коперника, видимые петлеобразные движения планет происходят в результате сложения действительных орбитальных движений Земли и наблюдаемых с нее планет.

    Вопрос: Какие нужны были изменения в философских взглядах людей на Землю, чтобы принять коперниканскую теорию вместо птолемеевой?

    Ответ: Больше нельзя было считать Землю уникальной, находящейся в центре всей Вселенной.

     Ученик: «Земля неподвижна», - когда-то учили.

                     «Земля неподвижна», - монахи твердили.

                      Коперник узнал о движенье земном.

                      Движенье Земли он увидел … умом.

                      Коперник глазам не поверил своим.

                       Причины нашел смены весен и зим.

                      «Да будет движенье Земли пол запретом», -

                       Сказано Римом особым декретом…   

     Ученик: Удивительны замысловаты видимые пути планет среди звезд. Двигаясь в одну сторону, они иногда неожиданно останавливаются и начинают пятиться назад. А потом вскоре попятное движение прекращается, и планета вновь идет в прежнем, прямом направлении. Видимые движения неравномерны. Все это вызывало недоумение древних и в свое время породило громоздкую систему Птолемея, преобразованную XVI в. Коперником. 

      Учитель: Однако и Копернику не удалось объяснить некоторые неравномерности в движении планет. Только Иоганн Кеплер (1571 – 1630) сумел внести полную ясность в законы движения планет, а Ньютон нашел теоретическое объяснение этим законам.

Современником Галилея был Иоганн Кеплер, в последующие годы получивший название «законодателя неба». Письмо Галилео Галилея немецкому ученому Иоганну Кеплеру, рассчитавшему орбиту планеты Марс. Падуя. 1610 год.

       «Кеплер!

         Я шлю тебе

         Весть о зрительной трубе.

         В тридцать раз

         Мне стало ближе наше небо.

         Наблюдал я ход планет.

         Видел горы на Луне…

         Звал ученых –

         Не пришли.

         Твердили: «Небыль!»

         Посмеемся, Кеплер мой,

         Великой трусости людской!

         Астрономы от старинных книг ослепли.

         Вокруг Юпитера в ночи

        Тоже луны различил.

        Жаль, что не было тебя

       Со мною, Кеплер!

P.S. Теперь я могу доказать, что прав Коперник».

    Ученик: Своим учением он шел против того, что казалось очевидным, а именно: что светила восходят и заходят, совершая обороты вокруг неподвижной Земли, с чем люди как бы сжились, и что освещалось с церковью и древними авторитетами. Земля же теперь представлялась небесным телом, одной из планет, а планеты – подобными Земле. Представление о глубоком различии «земного» и «небесного» разрушалось.           

    Учитель: Кеплер не сомневался в правильности основных положений учения Коперника, но он знал, что существуют расхождения предвычисленными и наблюдаемыми положениями планет. Чтобы ликвидировать это несоответствие, Кеплеру пришлось отказаться от кругового и равномерного движения планет. Для определения гелиоцентрических орбит планет он использовал результаты наблюдений датского астронома Тихо Браге (1546 – 1601). Особенно тщательно Кеплер изучал движение Марса. Итог его многолетних работ – открытие трех основных законов движения планет. Эти законы носят имя Кеплера.

    Ученик: Кеплер родился в маленьком Вюртембергском городке Вейле в семье бедных родителей. Он рано проявил свои математические способности и получил возможность поступить в университет. Будучи затем преподавателем математики, Кеплер познакомился с теорией Коперника и стал его убежденным сторонником. В 1600 г. Кеплер отправился в Прагу к известному в то время астроному Тихо Браге, который был замечательным наблюдателем, но не был сторонником системы Коперника. Свои наблюдения он проводил вначале в своей родной стране Дании. Там он построил на небольшом острове Вене замечательную для того времени астрономическую обсерваторию, названную им Уранибург. За 30 с лишним лет наблюдений Тихо Браге собрал богатейший материал весьма точных наблюдений над положениями планет, комет и звезд. В последние годы своей жизни был вынужден оставить остров Вен и обосновался в Праге, куда пригласил к себе Кеплера. Браге оставил все свои труды Кеплеру. Кеплер после девятилетнего упорного труда пришел к открытию законов истинного движения планет вокруг Солнца. Он изложил их в своей книге.

      Учитель: В этой книге Кеплер прежде всего устанавливает закон о неравномерности движения планеты по орбите. Затем излагает трудные поиски той истинной формы орбиты, которую описывает Марс вокруг Солнца. Он испытал много различных кривых и, наконец, нашел верное решение: орбиты Марса есть эллипс. Поместив в одном из фокусов Солнце, Кеплер получил полное совпадение наблюдений с теорией. Так Кеплер открыл первые два закона движения планет.

  Первый закон: Каждая планета обращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.

    Учитель: Точка орбиты, где планета приближается на наименьшее расстояние к Солнцу, называется перигелием, а самую отдаленную от центра Солнца точку орбиты планеты назвали афелием. Сумма расстояний в перигелии и афелии равна большой оси эллипса: r_max + r_min = 2a. Большая полуось земной орбиты называется астрономической единицей.

1 а. е. = 149,6x10⁶ км. Земля в перигелии 3 и 4 января приближается к Солнцу на минимальное расстояние 147 млн км, 3 и 4 июля (Земля в афелии) удаляется от Солнца на максимальное расстояние 153 млн км.

Рассмотрим важнейшие точки и линии эллипса.

а – большая полуось,
b – малая полуось,
F₁, F₂ – фокусы, 
r – радиус вектор,
А – афелий,
П – перигелий.

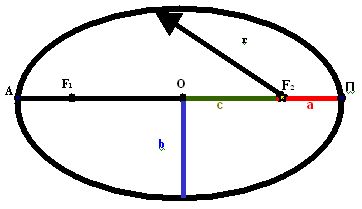
Степень вытянутости эллипса характеризуется эксцентриситетом е. 

е = с/а; где с – расстояние от центра эллипса до его фокуса, а – большая полуось.

При совпадении фокусов с центром (е = 0) эллипс превращается в окружность, при е = 1 становится параболой, при е > 1 – гиперболой.

Орбиты планет – эллипсы, мало отличаются от окружностей, так как их эксцентриситеты малы. Например, е_Земли=0,017, е_Марса= 0,091.

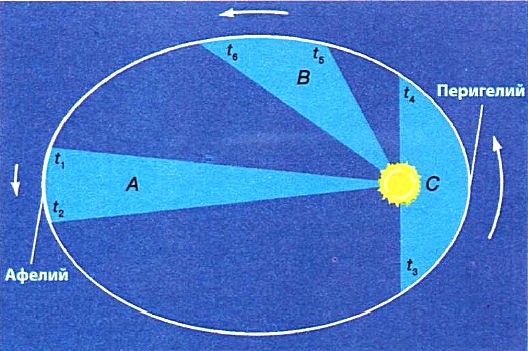
 Второй закон: Радиус-вектор планеты за равные промежутки времени описывает равные площади.

    Только через 10 лет появилось другое сочинение Кеплера, в котором он изложил третий, найденный им закон, устанавливающий зависимость между относительными расстояниями и периодами обращения планет вокруг Солнца. В результате этих почти двадцатилетних работ Кеплер дал теорию движения планет и тем создал основы важнейшего отдела новой астрономии – теоретической астрономии.

    Учитель: Главное следствие второго закона Кеплера состоит в том, что во время движения планеты по орбите со временем меняется не только расстояние планеты до Солнца, но и ее линейная и угловая скорости.

Самую большую скорость планета имеет в перигелии, когда расстояние до Солнца наименьшее, а самую маленькую — в афелии, когда расстояние наибольшее.

Второй закон Кеплера фактически определяет известный физический закон сохранения энергии: сумма кинетической и потенциальной энергии в замкнутой системе является величиной постоянной. Кинетическая энергия определяется скоростью планеты, а потенциальная — расстоянием между планетой и Солнцем, поэтому при приближении к Солнцу скорость планеты возрастает.

  Третий закон: Квадраты звездных периодов обращения планет относятся между собой как кубы больших полуосей их орбит.

                  (презентация)

      Ученик: Можно ли проверить законы Кеплера в школьных условиях?

     Учитель: Проверить первый закон трудно, так как нужно измерить расстояние от Земли до Солнца зимой и летом. Второй закон Кеплера может проверить любой из вас. Для проверки этого закона можно использовать календарь, вычислить длительность полугодия от 23 сентября до 21 марта и, наоборот, от 21 марта до 23 сентября. Если наша Земля вращалась бы с постоянной скоростью, то количество дней в двух полугодиях будет одинаковым. Так как скорость вращения Земли летом 29,36 км/с, а зимой 30,38 км/с, то количество дней в этих полугодиях разное. По второму закону Кеплера, зимой скорость Земли больше, а летом — меньше, поэтому лето в Северном полушарии длится чуть больше, чем зима, а в Южном полушарии, наоборот, зима немного длиннее лета. Значит, среднегодовая температура Северного полушария Земли вше, чем Южного полушария. В реальных условиях ни одна планета не движется по эллиптической орбите. Мы знаем, что законы Кеплера справедливы только для двух тел, обращающихся вокруг общего центра масс. В Солнечной системе обращаются вокруг Солнца большие планеты и множество малых тел, поэтому каждую планету притягивает не только Солнце — одновременно притягиваются между собой все эти тела. В результате такого взаимодействия разных по величине и направлению сил движение каждой планеты становится достаточно сложным. Такое движение называют возмущением. Орбита, по которой движется при возмущенном движении планета, не является эллипсом.

  Ученик: Законы Кеплера дают геометрическое представление планетных движений, но не дают им физического объяснения. Возникает вопрос: какая причина вызывает движение планет по эллипсам и заставляет радиусы-векторы описывать площади, пропорциональные времени?

    Учитель: Кеплеру было ясно, что такая причина должна существовать и что его законы являются следствием какого-то более общего закона. Кеплер предположил, что Солнце вращается вокруг оси в том направлении, в каком движутся планеты. Из вращающегося Солнца в плоскости его экватора выбрасываются «нематериальные истечения», которые захватывают планеты и заставляют их участвовать в круговом движении. Действие этих истечений Кеплер считал обратно пропорциональным первой степени расстояния. Наряду с этой фантастической гипотезой Кеплер высказывал правильные взгляды на силу тяготения. В эпоху Кеплера (начало XVII в.), когда еще не были созданы основы механики, эти глубокие мысли не получили дальнейшего развития; это было выполнено через полвека Ньютоном. Ньютон вывел свойства силы, управляющей движением планет, и доказал, что планеты и их спутники движутся под действием силы притяжения, величина которой обратно пропорциональна квадрату расстояния.

   Ньютон доказал, что каждый из законов Кеплера выражает особое свойство силы, управляющей движением планет. Второй закон Кеплера доказывает, что на планету действует сила, направленная к центру Солнца, т.е. сила солнечного притяжения.

  Первый закон доказывает, что сила солнечного притяжения, действующая на данную планету, обратно пропорциональна квадрату расстояния планеты от центра Солнца.

    Третий закон доказывает, что сила солнечного притяжения, действующая на разные планеты, обратно пропорциональна квадратам расстояний планет от Солнца.

   Задача: Первый закон Кеплера.

Наблюдая визуально-двойную звезду с сильно вытянутой эллиптической орбитой, астроном заметил, что яркий компонент лежит в центре эллипса, а не в его фокусе. Следует ли из этого, что нарушен 1-й закон Кеплера?

        Решение: Если орбита круговая, а ее видимая вытянутость вызвана лишь наклоном орбитальной плоскости к лучу зрения наблюдателя, то описанная ситуация вполне возможна без нарушения закона Кеплера.

    Учитель: Фантастика XVII века. В своем замечательном научно-фантастическом произведении «Сон, или Лунная астрономия» Иоганн Кеплер описал астрономические явления, якобы наблюдавшиеся с поверхности Луны. Если адаптировать его язык к современным терминам, то один из отрывков звучит так: «Луна состоит из двух полушарий: одно обращено к Земле, другое — в противоположную сторону. С первого всегда видна Земля, со второго Землю увидеть невозможно. Наблюдателям первого полушария кажется, что Земля на их небе неподвижна, но они легко могут заметить ее суточное вращение. На Луне происходит смена дня и ночи, однако, в отличие от Земли, день на Луне всегда равен ночи, их продолжительность не меняется в течение года». Верны ли сведения о Луне, приведенные Кеплером 400 лет назад?

        Решение: Сведения, приведенные Кеплером, практически верны. На лунном небе Земля почти неподвижна. Для наблюдателя на большей части лунной поверхности Земля не восходит и не заходит. Солнечные сутки на Луне (равные 29,5 земных суток) практически поровну делятся между восходом и заходом Солнца, как на Земле в дни равноденствий, поскольку плоскость лунного экватора составляет с плоскостью эклиптики угол всего в 1° 30'.

       Учитель: Новые законы Кеплера.

 Сформулируйте законы Кеплера для центральной силы, если ее значение изменяется пропорционально расстоянию: F ~ R.

            Решение:

1. Планеты движутся по эллипсам, в центрах которых — Солнце.

 2. За равные времена радиус-вектор заметает равные площади.

3. Период не зависит от размера орбиты.

    Учитель: Перигелийное расстояние Урана равно 18,4 а.е. Афелийное расстояние приблизительно равно 20,0 а.е. Чему равна большая полуось его орбиты?

          Решение:

Запишем условие задачи с использованием известных формул:

Q = a (1 – e) = 18,4 а.е.

Q = a (1 + e) =20,0 а.е.

Сложим обе части уравнения и разделим пополам:

A = (Q + q)/2

Откуда: a=19,2 а.е. Ответ: a=19,2 а.е.

Учитель: Какую половину эллиптической орбиты (e > 0) планета пройдет за меньшее время?

             Решение:

Соедините последовательно три точки:

1)точку на орбите между перигелием и афелием,

2)фокус эллипса, в котором находится Солнце,

3)точку на орбите, симметричную первой

и сравните площади под образовавшимися секторами.

Ответ: Ту, которая содержит перигелий.

     Учитель: Большая полуось орбиты Урана равна приблизительно 19,2 а.е. Не производя вычислений, оцените период обращения Урана вокруг Солнца.

       Решение: Возьмем квадратный корень из третьего закона Кеплера. Получим, что зависимость выглядит так : Та^3/2. Поэтому Т растет быстрее, чем а (быстрее, чем в случае Та). Ответ: 19 лет.

      Задача: Астероид Икар в перигелии подлетает к Солнцу на 0,19 а.е., а в афелии удаляется от него на 1,97 а.е. Чей период обращения вокруг Солнца больше – Земли или Икара?

    Решение: Воспользуемся формулой для большой полуоси через расстояния до перицентра и апоцентра: Икара.

a=(Q+q)/2; Откуда: a=1,08 а.е. Согласно третьему закону Кеплера квадраты периодов относятся как кубы больших полуосей. Большая полуось у Икара больше единицы, значит и период обращения больше года.

    Задача: Во сколько раз изменится сила притяжения, согласно Закону Всемирного тяготения, если массу центрального тела и расстояние до него уменьшить вдвое? (Ответы «> 1» обозначают увеличение силы, ответы «< 1» – уменьшение).

Решение: Запишем закон всемирного тяготения F=GM·m/R²; заменим М на М/2, а R на R/2 в правой части уравнения. Полученное выражение будет вдвое больше исходного. Ответ: в 2 раза.

     Задача: Снаружи или внутри Земли находится центр масс системы «Земля – Луна»?

          Решение: Запишем общую формулу для центра масс: Х_цм =

Из этой формулы и из простых соображений видно, что расстояние от центра масс до центров тел обратно пропорционально массам. Выведите эту формулу самостоятельно в качестве упражнения. Т.е. если Земля тяжелее Луны в 81 раз (взять соотношение в конце учебника), значит, расстояние от Земли до центра масс системы «Земля-Луна» равно x, а от Луны до центра масс – 81x. При этом условие на нахождение центра масс за пределами Земли будет выглядеть так: «Расстояние от Земли до Луны должно быть больше, чем 82R⊕. Подставим радиус Земли и получим, что это более, чем 520 000 км. Так далеко Луна не отходит от Земли (см. апогей для лунной орбиты), поэтому центр масс системы Земля-Луна все время находится внутри Земли. Ответ: Всегда внутри.

     Задача: Как отличить по внешнему виду планету от звезды.

Ответ: Внешние отличия следующие: звезды мерцают, а свет от планет ровный, спокойный. При наблюдении в телескоп у планет видны диски, а звезды выглядят светящимися точками.

    Задача: Какую планету, хорошо видимую невооруженным глазом, трудно отыскать на небе? Почему?

Ответ: Меркурий – самую близкую к Солнцу планету. Из-за своей близости к Солнцу эта планета большую часть года видна на светлом фоне зари и плохо заметна.

    Задача: Вычислите период обращения Нептуна вокруг Солнца, зная, что его среднее расстояние от Солнца равно 30 а. е.

          Решение: Воспользуемся третьим законом Кеплера:

,

где T_H – звездный период Нептуна, a_H – среднее расстояние от Солнца (большая полуось орбиты),  – звездный период Земли,  – большая полуось земной орбиты (1 а. е.)

Тогда

.

5. Определите расстояние от Солнца до Урана, зная, что период обращения Урана вокруг Солнца равен 84 г.

По третьему закону Кеплера

,

откуда

.

      Задача: Синодический период планеты 500 сут. Определите большую полуось ее орбиты и звездный период обращения.

      Решение:

Большую полуось орбиты можно определить из третьего закона Кеплера:

, откуда ,

а звездный период – из соотношения между сидерическим и синодическим периодами:

 (если планета внешняя)

 (если планета внутренняя).

Тогда  (для внешней) и  (для внутренней).

 (внешняя планета)

 (внутренняя планета)

 – планета внешняя,

 – планета внутренняя.

Ученик: Почему спутники удерживаются на орбитах около своих спутников?

 Учитель: На своей орбите около планеты спутник удерживается вследствие сложения двух движений – прямолинейного движения по инерции и движения к планете, вызываемого ее притяжением. 

 Учитель: Все космические тела от планет до галактик движутся по закону всемирного тяготения, который был открыт Ньютоном. Понадобился гений Ньютона, чтобы понять, что именно его закон объясняет, почему предметы падают на Землю, почему по орбитам движутся Луна и планеты. Этот закон называется законом всемирного тяготения, а это означает, что он справедлив для всех тел во Вселенной. Отталкиваясь от основных принципов, Ньютон обобщил и математически обосновал законы планетных движений Кеплера. Законы Кеплера определяют форму орбиты, скорость движения планет Солнечной системы и их периоды обращения вокруг Солнца. Во второй половине ХХ века было замечено, что некоторые звезды, которые находятся достаточно далеко от центра нашей Галактики, не подчиняются этому закону Кеплера. Это означает, что мы не всё знаем о том, как действует гравитация в размерах нашей Галактики. Одним из возможных объяснений того, почему далекие звезды движутся быстрее, чем это требуется по третьему закону Кеплера, оказалось следующее: мы видим не всю массу Галактики. Значительная ее часть может состоять из вещества, которое не наблюдаемо нашими приборами, не взаимодействует электромагнитно, не излучает и не поглощает свет, а участвует только в гравитационном взаимодействии. Такое вещество было названо скрытой массой или темной материей. Проблемы темной материи – это одна из основных проблем физики XXI века.

Подведение итогов урока.

                 Литература:

1. Моше Д. Астрономия: Кн. для учащихся. пер. с анг. / Под ред. А.А. Гурштейна. – М.: Просвещение, 1985. -255 с.

2. Малахова Г.И. Дидактический материал по астрономии: Пособие для учителя. -3-е изд., перераб. - М.: Просвещение/ Г.И. Малахова, Е.К. Страут., 1989.- 96 с.

3. Полак И.Ф. Курс общей астрономии/И.Ф. Полак; Государственное издательство технико-теоретической литературы. – М.: 1955 - 371 с.

4. Орлов В.Ф. «300 вопросов по астрономии»; Издательство «Просвещение», 1967г.

5. Разбитная Е.П. Программированные задания по астрономии: Пособие для учителей. – М.: Просвещение, 1981. - 80 с.

6. Дагаев М.М., Чаругин В.М. Книга для чтения по астрономии: Астрофизика: Учеб. пособие для учащихся 8-10 кл. – М.: Просвещение, 1988. - 207 с.

7. Чаругин В.М. Астрономия 10-11 классы:учеб. для общеобразоват. организаций: базовый уровень/ В.М. Чаругин.- М.: Просвещение, 2018.-144 с.

8. Воронцов-Вельяминов Б.А.: Астрономия. Базовый уровень 11 класс: учебник/Б.А. Воронцов-Вельяминов, Е. К. Страут. -5 изд., пересмотр. -М.: Дрофа, 2018. -238.

Скачано с www.znanio.ru