Законы Кирхгофа. Работа и мощность электрического тока. Закон Джоуля - Ленца. Коэффициент полезного действия источника тока.

29 №Сабақ / Урок № 29

Сабақ жоспары / План урока

 

Сабақтың тақырыбы / Тема урока

Законы Кирхгофа. Работа и мощность электрического тока. Закон Джоуля - Ленца. Коэффициент полезного действия источника тока.

 

Законы Кирхгофа

Разветвленной цепью называется электрическая цепь, имеющая узлы.

Узлом называется точка, в которой сходится более чем два проводника. Ток, текущий к узлу, принято считать положительным, а ток, текущих от узла, считается отрицательным.

Ветвь – участок цепи, обтекаемый одним и тем же током.

Контур – замкнутая конфигурация цепи, проходящая через несколько узлов и ветвей.

При анализе разветвленной цепи следует обозначать с одним индексом ток, протекающий по всем последовательно соединенным элементам от одного узла до другого. Направление каждого тока выбирается произвольно.

При составлении уравнений второго правила Кирхгофа токам и ЭДС. нужно приписывать знаки в соответствии с выбранным (как вам удобно) направлением обхода:

• ток принято считать положительным, если он совпадает с направлением обхода, и отрицательным, если он направлен против этого направления;

• ЭДС считается положительной, если ее действие (создаваемый ею ток) совпадает с направлением обхода.

Количество уравнений первого правила Кирхгофа должно быть на одно меньше количества узлов в данной цепи.

Количество независимых уравнений второго правила Кирхгофа должно быть таким, чтобы общее количество уравнений оказалось равным количеству различных токов. Каждый новый контур при этом должен содержать хотя бы один участок цепи, не вошедший в уже рассмотренные контуры. Часто применяется смешанное соединение проводников: использование последовательного и параллельного соединения проводников в одной цепи.

Метод непосредственного применения 1 и 2 законов Кирхгофа.

Первый закон Кирхгофа – «Алгебраическая сумма токов, проходящих через узел равна нулю»:

Σ Iк = 0

Второй закон Кирхгофа - «В замкнутом контуре алгебраическая сумма падений напряжений на сопротивлениях равна алгебраической сумме ЭДС того же контура»:

Σ Uк = Σ Eк.

Алгоритм решения задач этим методом:

1.      Определить общее число уравнений. Оно равно числу ветвей:

m = в.

2. Определить число уравнений по первому закону Кирхгофа. Оно равно числу узлов минус 1:

m₁= у – 1

3. Определить число уравнений по второму закону Кирхгофа:

m₂ =m – m₁

4. Указать произвольно направления токов в ветвях.

5. Составить уравнения по первому закону Кирхгофа.

6. Указать произвольно направления обхода независимых контуров. Независимым называется контур, в котором хотя бы одна ветвь не входит в другие контуры.

7. Составить уравнения по второму закону Кирхгофа.

8. Решить систему уравнений.

9. Скорректировать направления токов в ветвях. Если ток получился со знаком минус, изменить его направление на противоположное.

10. Проверить результат по уравнению баланса мощностей. Сумма мощностей всех источников, работающих в режиме генерирования, равна сумме мощностей всех потребителей энергии.

Если ЭДС источника и ток через него совпадают по направлению – источник работает в режиме генерирования.

Если они противоположны по направлению - источник работает в режиме потребления.

Пример (Рисунок 1).

 

Рисунок 1 - Метод непосредственного применения 1 и 2 законов Кирхгофа

 

Определить токи в ветвях методом непосредственного применения законов Кирхгофа:

1.       Общее число уравнений: m = 3.

2.      Число уравнений по 1-му закону Кирхгофа: m₁ = 2 – 1 = 1.

3.      Число уравнений по 2-му закону Кирхгофа: m₂ = 3 – 1 =2.

4.      Указать направления токов в ветвях (сплошными стрелками).

5.      Составить уравнение по 1-му закону Кирхгофа: I₁+ I₂ – I₃ = 0

6.      Указать направления обхода контуров.

7.      Составить уравнения по 2-му закону Кирхгофа.

8.      Решить систему уравнений.

Результат: I₁ = 14 А; I₂ = - 15 А; I₃ = - 1 А.

9.      Скорректировать направления токов I₂ и I₃ (стрелки пунктирной линией).

10.  Проверить результаты. Оба источника работают в режиме генерирования.

ΣP_ист =Σ P_потр

E₁ I₁ + E₂ I₂ = R₁ I₁ ² + R₂ I₂² + R₃ I₃²

2080 = 2080

Получилось тождество, следовательно, решение верно.

Недостаток метода – при большом количестве ветвей, большое число уравнений.

Метод контурных токов

Предполагается, что все независимые контуры обтекаются контурными токами. Задача сводится к определению контурных токов и последующим определением токов в ветвях.

Алгоритм решения задач методом контурных токов:

1. Выбрать независимые контуры.

2. Указать (по часовой стрелке) направления контурных токов.

3. Составить систему канонических уравнений.

4. Определить собственные сопротивления контуров (R₁₁, R₂₂, R₃₃). Они равны арифметической сумме всех сопротивлений, входящих в контур.

5. Определить общие сопротивления смежных контуров (R₁₂ = R₂₁, R₁₃ = R₃₁, R₃₂ = R₂₃). Они равны сопротивлениям ветвей на границе контуров со знаком минус. Если контуры не граничат, то эти сопротивления равны 0.

6. Определить собственные ЭДС контуров (E₁₁,E₂₂, E₃₃). Они равны алгебраической сумме ЭДС, входящих в контур. Если ЭДС направлена против контурного тока, она берется со знаком минус.

7. Решить систему уравнений.

8. Если контурный ток получился со знаком минус, изменить его направление на противоположное.

9. Определить токи в ветвях.

10. Проверить результат по уравнению баланса мощностей.

Пример

Определить токи в ветвях методом контурных токов (Рисунок 2).

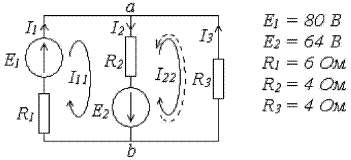
Рисунок 2 - Метод контурных токов

 

1. Выбирать количество контуров, согласно примеру 2 контура.

2. Указать направления контурных токов (сплошными стрелками).

3. Составить систему канонических уравнений:

4. Определить собственные сопротивления контуров:

R₁₁ = R₁ + R₂ = 10 Ом;

R₂₂ = R₂ + R₃ = 8 Ом;

5. Определить общие сопротивления смежных контуров:

R₁₂ = R₂₁ = - R₂ = - 4 Ом.

6. Определить собственные ЭДС контуров:

E₁₁ = E₁ + E₂ = 144 В; E₂₂ = - E₂ = - 64 В.

7. Решить систему уравнений:

I₁₁ =14 А; I₂₂ = - 1 А

8. Изменить направление тока I₂₂  на противоположное (стрелка пунктирной линией).

9. Определить токи в ветвях: I₁ = I₁₁ =14 А; I₂ = I₁₁ + I₂₂ = 15 А; I₃ = I₂₂ =1 А.

10. Проверить результат по уравнению баланса мощностей. Оба источника работают в режиме генерирования.

ΣP_ист =Σ P_потр

E₁ I₁ + E₂ I₂ = R₁ I₁² + R₂ I₂² + R₃ I₃²

2080 = 2080

Получается тождество, следовательно, решение верно.

Метод позволяет уменьшить количество уравнений при небольшом количестве независимых контуров.

Недостаток – метод применяется только для расчета линейных цепей.

 

Работа и мощность электрического тока. Закон Джоуля - Ленца

При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном участке совершает работу:

 

 где U = Δφ₁₂ – напряжение. Эту работу называют работой электрического тока.

Если обе части формулы выражающей закон Ома для однородного участка цепи с сопротивлением R, умножить на IΔt, то получится соотношение:

 

Это соотношение выражает закон сохранения энергии для однородного участка цепи.

При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном участке совершает работу.

 

Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике.

Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца.

Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:

 

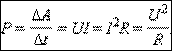Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).

Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. Закон Ома для полной цепи записывается в виде

 

Умножив обе части этой формулы на Δq = IΔt, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:

 

Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. Закон Ома для полной цепи записывается в виде

 

Умножив обе части этой формулы на Δq = IΔt, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:

 

Первый член в левой части ΔQ = R I²Δt – тепло, выделяющееся на внешнем участке цепи за время Δt, второй член ΔQ_ист = r I²Δt – тепло, выделяющееся внутри источника за то же время. Выражение ℰIΔt равно работе сторонних сил ΔA_ст, действующих внутри источника.

При протекании электрического тока по замкнутой цепи работа сторонних сил ΔA_ст преобразуется в тепло, выделяющееся во внешней цепи (ΔQ) и внутри источника (ΔQ_ист).

 

Следует обратить внимание, что в это соотношение не входит работа электрического поля. При протекании тока по замкнутой цепи электрическое поле работы не совершает; поэтому тепло производится одними только сторонними силами, действующими внутри источника. Роль электрического поля сводится к перераспределению тепла между различными участками цепи.

Внешняя цепь может представлять собой не только проводник с сопротивлением R, но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под R нужно понимать эквивалентное сопротивление нагрузки. Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, но и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем. Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение.

В процессе перемещения зарядов внутри замкнутой цепи, источником тока совершается определенная работа. Она может быть полезной и полной. В первом случае источник тока перемещает заряды во внешней цепи, совершая при этом работу, а во втором случае – заряды перемещаются во всей цепи. Коэффициент полезного действия есть отношение полезной работы к затраченной

 

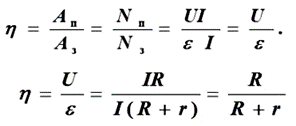
В этом процессе большое значение имеет КПД источника тока, определяемого, как соотношение внешнего и полного сопротивления цепи. При равенстве внутреннего сопротивления источника и внешнего сопротивления нагрузки, половина всей мощности будет потеряна в самом источнике, а другая половина выделится на нагрузке. В этом случае коэффициент полезного действия составит 0,5 или 50%.

 

Домашнее задание:

· Прочесть «Физика 10 класс. 2 часть» Б.Кронгарт, Д.Казахбаева, О.Иманбеков, Т.Қыстаубаев - Мектеп. 2019, с. 78-86.

· Составить опорный конспект – формулы, алгоритмы решения и примеры законов Кирхгофа, рисунки обязательно.

· Из раздела «Решайте» с. 84 №2 решить задачу, записать в тетрадь с фотографировать, поместить в ворд и прикрепить на портал.

· Скачано с www.znanio.ru