Занимательные задачи по теме «Теорема Пифагора» (8 класс)
Теорема Пифагора по праву считается самой важной в курсе геометрии и заслуживает пристального внимания. Она является основой решения множества задач. Поэтому для формирования понимания значимости теоремы Пифагора при изучении как геометрии, так и других дисциплин, умений применять теорему Пифагора к решению задач я предлагаю восьмиклассникам индивидуальные разноуровневые задачи, требующие творческого подхода в решении и оформлении. Решение таких занимательных задач помогает также воспитывать у учащихся интерес к предмету: математика уже не кажется им сухой и скучной наукой, дети видят, что и здесь нужны выдумка, полет фантазии, творческие способности.
Задача №1. Древнеиндийская задача.
Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос одиноко,
И ветер порывом
Отнёс его в сторону. Нет
Боле цветка над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
“Как озера вода здесь глубока?”
Какова глубина в современных единицах длины (1 фут ≈ 0,3 м) ?
Решение.
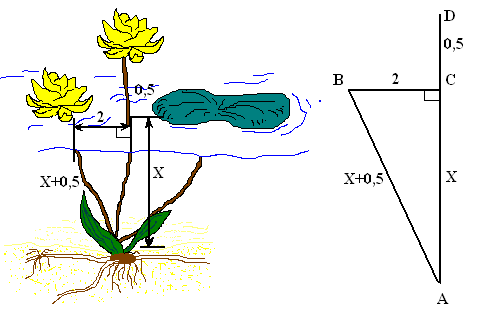
Выполним чертёж к задаче и обозначим глубину озера АС =Х, тогда AD = AB = Х + 0,5 .
Из треугольника ACB по теореме Пифагора имеем AB2 – AC2 = BC2,
(Х + 0,5 )2 – Х2 = 22,
Х2 + Х + 0,25 – Х2 = 4,
Х = 3,75.
Таким образом, глубина озера составляет 3,75 фута.
3, 75 ∙ 0,3 = 1,125 (м)
Ответ: 3,75 фута или 1, 125 м.
Задача №2. Задача индийского математика XII в. Бхаскары.
На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки, осталось три фута всего от ствола. Прошу тебя, скоро теперь мне скажи: у тополя как велика высота?
Решение.
|
|
Пусть АВ – высота ствола. По теореме Пифагора имеем СD= АВ = АС + АD, АВ = 3 + 5 =8. |
.Ответ: 8 футов.
Задача №3. Задача арабского математика XI в.
На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?
Решение.
|
|
Итак,
в треугольнике АDВ: АВ2=ВD2+АD2=302+Х2=900+Х2; Но АВ=АС, так как обе птицы пролетели эти расстояния за одинаковое время. Поэтому АВ2=АС2, 900+Х2=2900-100Х+Х2, АD=20. Значит, рыба была на расстоянии 20 локтей от большой пальмы. |
Ответ: 20 локтей.
Задача №4. Египетская задача.
На глубине 12 футов растет лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну.
Решение.
|
|
Пусть АВ = АС – длина стебля. Из ∆АDС по теореме Пифагора СD
= |
Ответ: 5 футов.
Задача №5.
Бамбуковый ствол в 9 футов высотой переломлен бурей так, что если верхнюю часть его пригнуть к земле, то верхушка коснется земли на расстоянии 3 футов от основания ствола. На какой высоте переломлен ствол?
Решение.
|
|
Пусть АВ=9 – высота ствола, искомая высота АС=Х, тогда СК = 9 - Х. Из ∆САК по теореме Пифагора СК2 = АС2 + АК2; (9 – Х)2 = Х2 + 32, 81 – 18Х + Х2 = Х2 + 9, 18Х = 72, Х = 4. Значит, ствол переломлен на высоте 4 футов. |
Ответ: 4 фута.
Задача №6.
В центре квадратного пруда, имеющего 10 футов в длину и ширину, растет тростник, возвышающийся на один фут над поверхностью воды. Если его пригнуть к берегу, к середине стороны пруда, то он своей верхушкой достигнет берега. Какова глубина пруда в современных единицах длины (1 фут ≈ 0,3 м)?
Решение.
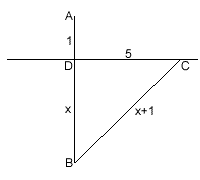
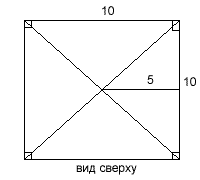
Обозначим глубину озера ВD = х, тогда АВ = ВС = х + 1 –
длина тростника. Из ∆ВDС по теореме Пифагора СD2 =
СВ2 –ВD2,
52 = (х + 1)2 – х2,
25 = х2 + 2х + 1 – х2,
2х = 24,
х = 12.
Значит, глубина пруда 12 футов. 12 ∙ 0,3 = 3,6 (м).
Ответ: 3,6 м.
Задача №7.
Эскалатор метрополитена имеет 17 ступенек от пола наземного вестибюля до пола подземной станции. Ширина ступенек 40 см, высота 20 см. Определите а) длину лестницы, б) глубину станции по вертикали.
Решение.
|
|
а) Пусть АВ – длина лестницы из 17 ступенек. Из ∆АКD по теореме Пифагора АD = АВ = 45 ∙ 17 = 765 (см) = 7, 65 (м). б) ВС = 40 ∙ 17 = 680 (см). Из ∆АСВ по теореме Пифагора АС = |
(см),
(см)
= = 3,5 (м).Ответ: длина лестницы 7, 65 м, глубина станции 3,5 м.
Задача №8.
Параллельно прямой дороге на расстоянии 500м от неё расположена цепь стрелков. Расстояние между крайними стрелками равно 120 м, дальность полёта пули 2800 м. Какой участок дороги находится под обстрелом?
Решение.
|
|
Из ∆АНD по теореме Пифагора АН = АВ = 2 ∙ АН + НК, АВ = 2 ∙ 2,755 + 0,12 ≈ 5,63 (км). |
(км),Ответ: 5,63 км.
Задача №9.
Пловец поплыл от берега реки, всё время гребя в направлении по перпендикуляру к берегу (берега реки считаем параллельными). Плыл он, приближаясь к противоположному берегу со скоростью 3 км/ч. Через 5 мин. он был на противоположном берегу. Узнайте, на каком расстоянии от мести начала заплыва он вышел на противоположном берегу, считая скорость течения всюду равной 6 км/ч.
Решение.
|
|
Пловец
приближался к противоположному берегу со скоростью АВ =
50 ∙ 5 = 250 (м). Скорость течения реки АС
= ≈ 250 ∙ 2,24=560 (м) |
Ответ: 560 м.
Задача №10.
Вы плывёте на лодке по озеру и хотите узнать его глубину. Нельзя ли воспользоваться для этого торчащим из воды камышом, не вырывая его?
Решение.
|
|
Слегка отклонив камыш и держа его в натянутом состоянии, замерим расстояние а между точками А и В, в которых камыш пересекает поверхность воды соответственно в вертикальном и наклоненном положении. Возвратим камыш в исходное положение и определим высоту в над водой, на которую поднимется при этом точка В наклонённого камыша, заняв исходное положение С. Тогда обозначив через D основание камыша, а через х – искомую глубину АD, из прямоугольного ∆АВD по теореме Пифагора находим х2+а2= (х+в)2, х2+а2= х2+2хв+в2 2хв=а2-в2, х= |
Задача №11.
Как далеко видно с маяка данной высоты над уровнем моря?
Решение.
|
|
Если
обозначить через Н высоту маяка, а через R радиус Земли
(R≈6400 км), то искомое расстояние будет равно S= При Н=125 м S ≈ 40 км. |
Ответ: с высоты маяка в 125 м обозревается расстояние в 40 км.
Задача №12.
Вертолет поднимается вертикально вверх со скоростью 4 м/с. Определите скорость вертолета, если скорость ветра, дующего горизонтально, равна 3 м/с.
Решение.
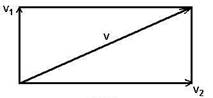v2 =
32 + 42 = 25
v = 5.
Ответ: 5 м/с.
Занимательные задачи по теме «Теорема
Х = 3,75. Таким образом, глубина озера составляет 3,75 фута
На глубине 12 футов растет лотос с 13-футовым стеблем
Значит, глубина пруда 12 футов
Пловец приближался к противоположному берегу со скоростью , значит ширина реки
Если обозначить через Н высоту маяка, а через
© ООО «Знанио»
С вами с 2009 года.
