
Змішані стратегії в біматрічних іграх
У приведених прикладах описані ситуації, в яких інтереси гравців не співпадають. Встає питання про те, які рекомендації необхідно дати ігрокам для того, щоб модельована конфліктна ситуація вирішилася. Іншими словами, що ми розумітимемо під рішенням біматрічної гри?
Спробуємо відповісти на це питання так: унаслідок того, що інтереси гравців не співпадають, нам потрібно побудувати таке (компромісне) рішення, яке б в тому або іншому, але в однаковому сенсі задовольняло обох гравців.
Не намагаючись відразу виражати цю думку зовсім точно, скажімо – спробуємо знайти якусь рівноважну ситуацію, явне відхилення від якої одного з гравців зменшувало б його виграш.
Подібне
питання ми ставили і при розгляді матричних ігор. Нагадаємо, що виникає при
розробці мінімаксного підходу поняття рівноважної ситуації приводило нас до
пошуку сідловок точки, яка, існує не завжди – звичайно, якщо обмежуватися
тільки чистими стратегіями ігроків А і В, тобто стратегіями ![]() .
.
Проте при розв’язанні матричної гри шляхом переходу до змішаних стратегій, тобто до такої поведінки гравців, при якій вони чергують (чисті) стратегії з певними частотами:
гравець А – стратегії A1,..., Ат з частотами р1,..., рт, де
![]()
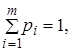
а гравець В – стратегії В1,...., Вn, с частотами q1,..., qn, де
![]()
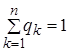
з'ясувалося, що в змішаних стратегіях рівноважна ситуація завжди існує. Іншими словами, будь-яка матрична гра в змішаних стратегіях розв’язується.
Тому, розглядаючи тут біматричні ігри, розумно спробувати відразу ж перейти до змішаних стратегій гравців (цим ми припускаємо, що кожна гра може бути багато разів повторена в незмінних обставинах).
У
матричному випадку змішування стратегій приводило до розширення можливостей
виплат в тому сенсі, що розрахунок будувався з обчислення середніх виграшів
гравців А і В, які визначалися по елементах платіжної матриці А і вірогідності
![]() і
і ![]() :
:
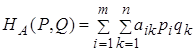 ,
,
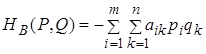
При змішаних стратегіях в біматрічних іграх також виникають середні виграші гравців А і В, визначувані за правилами, в яких вже немає ніякої дискримінації гравця В:
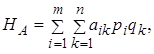 ,
, 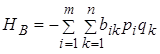
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.