Բազմանկյունների և բազմանիստերի պատկերումը

Բազմանկյունների և բազմանիստերի պատկերումը

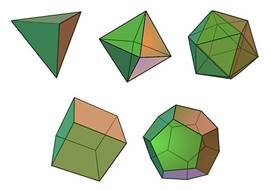
      Բնության մեջ հանդիպող և բնական կամ արհեստական ծագում ունեցող պինդ մարմինների տարբեր տեսակների շարքում կարևոր դեր են խաղում բազմանիստերը: Բազմանիստ ասելով հասկանում ենք սահմանափակ մարմին, որի մակերևույթը կազմված  է վերջավոր քանակով հարթ բազմանկյուններից: Այս նախադասությունը խիստ մաթեմատիկական չէ: Մենք ուղղակի սահմանում ենք բազմանիստը՝ օգտվելով <<մարմին>> հասկացությունից:

     Բազմանիստերի (և այլ մարմինների) հատկությունները մենք հիմնականում կուսումնասիրենք մտահայեցորեն՝ օգտագործելով նրանց հարթ պատկերումները (այսինքն՝ հարթության վրա գտնվող նրանց պատկերները):

     Մենք արդեն գործ ենք ունեցել բազմանիստերի հարթ պատկերումների հետ և լուծել ենք խնդիրներ, որոնցում պահանջվում էր կատարել այս կամ այն կառուցումները նրանց պատկերների վրա: Այդ գործողություններում մենք օգտվել ենք միայն ուղիղների և հարթությունների հիմնական հատկություններից և այն կարևոր փաստից, որ ուղղի պատկերը միշտ ոիղիղ է: Ըստ այդմ, բազմանիստի գծապատկերը եղել է խնդրի պայմանի մի մասը և չի քննարկվել, թե ինչպես էայն ստացվել:

     Այս գլխում մենք կդիտարկենք բազմանիստերի (նաև այլ մարմինների) հարթ պատկերների կառուցման որոշ հիմնական սկզբունքներ: Նախ և  առաջ ձևակերպենք գլխավոր սկզբունքը. տարածական առարկաների հարթ պատկերները ստացվում են պրոյեկտման միջոցով:  Այսպես՝ հարթության վրա բազմանկյան պրոյեկցիան հանդիսանում է նաև նրա պատկերը: Դրանից հետևում է ուղղի ( հատվածի) պատկերը կլինի ուղիղ ( հատված): Անենք մի վերապահում. ուղիղը կարող է պրոյեկտվել նաև կետի, այդ դեպքում նրա պատկեր է հանդիսանում կետը:Ընդհանուր դեպքում զուգահեռ ուղիղների պատկերները զուգահեռ ուղիղներ են: ( Զուգահեռ ուղիղները կարող են պրոյեկտվել մի ուղղի և անգամ երկու կետի ): Ընդհանրապես, բազմանկյան պրոյեկցիան (պատկերը) նույն  քանակով կողմեր ունեցող բազմանկյուն է: ( Մասնավոր դեպքերում հարթ բազմանկյան պրոյեկցիան կարող է լինել հատված՝ վերասերված բազմանկյուն): 

     Պրոյեկտման հիմնական հատկություններից հետևում է, որ զուգահեռագծի պատկերը նույնպես զուգահեռագիծ է ( հնարավոր է վերասերված զուգահեռագիծ, այսինքն՝ հատված): 

    Օգտակար է իմանալ, որ տրված եռանկյան պատկեր կարող է լինել ցանկացած եռանկյանը նման եռանկյունի: Մասնավորապես ցանկացած եռանկյուն կարելի է պրոյեկտել կանոնավոր եռանկյան վրա, այսինքն՝ կանոնավոր եռանկյունը կարող է լինել ցանկացած եռանկյան պատկեր:

    Հիշեցնենք, որ բազմանիստ ասելով հասկանում ենք սահմանափակ մարմին, որի մակերևույթը կազմված է վերջավոր քանակով բազմանկյուններից, որոնք կոչվում են բազմանիստի նիստեր: Նիստի եզրը կազմված է ուղղի հատվածներից, որոնք կոչվում են բազմանիստի կողեր: Յուրաքանչյուր կող պատկանում է երկու հարևան նիստերի: Կողի ծայրակետերը բազմանիստի գագաթներն են: 

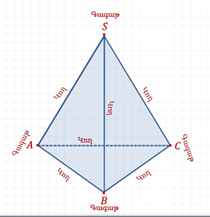
    Բազմանիստի պատկերը հարթության վրա բաղկացած է նրա կողմերի պատկերներից (որոնք ստացվում զուգահեռ պրոյեկտման միջոցով): Ընդսմին բոլոր կողերը բաժանվում են երկու տեսակի՝ տեսանելի և անտեսանելի: Տեսանելի կողերը պատկերում են անընդհատ հատվածներով, անտեսանելիները՝ ընդհատվող: