Կոտորակագծային ֆունկցիա

Կոտորակագծային ֆունկցիա

     Կոտորակագծային կոչվում է y=(ax+b)/(cx+d) ֆունկցիան, որտեղ  a-ն, b-ն, c-ն, d-ն իրական թվեր են:

    Համարենք, որ c≠0  և  ad≠bc, քանի որ c=0 դեպքում ստանում ենք գծային ֆունկցիա, իսկ a⋅d=b⋅c դեպքում՝ ֆունկցիան հաստատուն է իր որոշման տիրույթում՝ x≠−d/c:

    Պարզագույն կոտորակագծային ֆունկցիան մեզ ծանոթ y=1/x ֆունկցիան է, որի գրաֆիկը հիպերբոլ է:

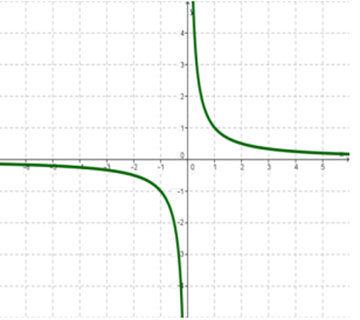
Հիշենք y=1/x ֆունկցիայի հատկությունները:

1. Ֆունկցիայի որոշման տիրույթը D=(−∞;0)∪(0;+∞) բազմությունն է:

2. Ֆունկցիայի արժեքների բազմությունը E(y)=(−∞;0)∪(0;+∞) բազմությունն է:

3. Եթե x>0, ապա y>0: Եթե x<0, ապա y<0:

4. Ֆունկցիան նվազում է (−∞;0) և (0;+∞) միջակայքերի վրա:

5. Ֆունկցիան ոչ վերևից, ոչ էլ ներքևից սահմանափակ չէ:

6. Ֆունկցիան չունի ոչ մեծագույն, ոչ էլ փոքրագույն արժեքներ:

7. Ֆունկցիան անընդհատ է (−∞;0) և (0;+∞) միջակայքերում, իսկ x=0 կետում խզվում է: