1 математического моделирования_9класс_Приложение_2час_рус (2)

Приложение 1.

Г.   Поделить учащихся на две группы по жребию. В корзину положить два вида карточек с рисунками. По рисунку распределить учащихся. Раздать постеры и маркеры.

1 группа. Задание:

Написать на постере алгоритм решения задач на движение.

Алгоритм решения задач на движение

1. Ввести неизвестные величины.

2. Составить краткую запись задачи в таблице (скорость, путь, время).

3. Исходя из условия задачи, составить систему двух уравнений с двумя неизвестными.

4. Решить систему уравнений, исключив те корни, которые не подходят по условию задачи.

5. Записать ответ по вопросу задачи.

2 группа. Задание:

Написать алгоритм решения задач на производительность.

Алгоритм решения задач на производительность

1.Ввести неизвестные величины.

2. Составить краткую запись задачи в таблице (производительность, работа, время).

3. Исходя из условия задачи, составить систему двух уравнений с двумя неизвестными.

4. Решить систему уравнений, исключив те корни, которые не подходят по условию задачи.

5. Записать ответ по вопросу задачи.

          Картинка №1                                                               Картинка №2

Приложение 2

Г.  Первичное закрепление. 

Задание. 1 группы.

Расстояние между двумя пристанями 60 км. Теплоход проходит это расстояние по течению и против течения за 5,5 ч. Найдите скорость теплохода в стоячей воде и скорость течения, если одна из них больше другой на 20 км/ч.

Дескриптор:

1.Отмечает скорость теплохода и течение реки.

2.Составляет математическую модель.

3. Составляет выражение по условию что теплоход проходит это расстояние по течению и против течения реки за 5,5 ч и скорость катера больше скорости течения реки.

4.Составляет систему двух уравнений с двумя неизвестными.

5.Определяет скорость теплохода и течения реки, указывает ед.изм.

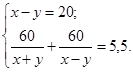Решение:

Ответ: 22 км/ч – скорость теплохода, 2 км/ч – скорость течения реки.

Задание. 2 группы.

Двое рабочих могут выполнить задание за 12 дней. Если сначала один из них сделает половину всей работы, а потом остальное сделает другой, то им потребуется 25 дней. За сколько дней каждый рабочий, работая один, может выполнить задание?

Дескриптор:

1.Отмечает производительность 1-го и 2-го рабочего .

2.Составляет математическую модель.

3.Указывает производительность, работу и время.

4.Составляет систему двух уравнений с двумя неизвестными.

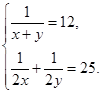Решение:

Ответ: Один рабочий выполнит всю работу за 30 дней, а другой за 20 дней.

Приложение 3

Парная работа.

№1.

Из двух пунктов M и N выехали навстречу друг другу два автомобиля. Один пришел в N через 1 ч 15 мин после встречи, а другой – в M через 48 мин после встречи. Расстояние между пунктами 90 км. Найдите скорости автомобилей.

Решение:

1.       Пусть V1 (км/ч) – скорость первого автомобиля,
              V2 (км/ч) – скорость второго автомобиля,
               t (ч) – время до встречи автомобилей.

2.       То расстояние, которое первый автомобиль проехал за t часов, второй автомобиль проехал за 48 минут.

3.       То расстояние, которое второй автомобиль проехал за t часов, первый автомобиль проехал за 1 ч 15 мин.

4. 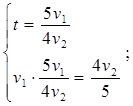      После встречи автомобили вместе проехали 90 км.

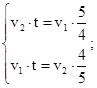
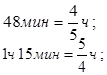
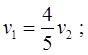
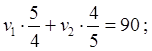
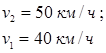
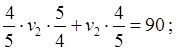
Ответ: Скорость первого автомобиля 40 км/ч,
       скорость второго автомобиля 50 км/ч.

№2.

Два туриста идут навстречу друг другу из пунктов A и B. Первый вышел из А на 6 ч позже, чем второй из В, и при встрече оказалось, что он прошел на 12 км меньше, чем второй. Продолжая движение с той же скоростью, первый пришел в В через 8 ч, а второй – в А через 9 ч после встречи. Найдите скорость каждого туриста.

Решение:

1.       Пусть V1 (км/ч) – скорость первого туриста,
              V2 (км/ч) – скорость второго туриста,
               t (ч) – время до встречи автомобилей.

2.       То расстояние, которое первый турист прошел за
(t-6) часов, второй турист прошел за 9 часов.

3.       То расстояние, которое второй турист прошел за t часов, первый турист прошел за 8 часов.

4.       До встречи первый турист прошел на 12 км меньше, чем второй.

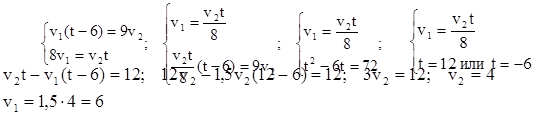
Ответ: Скорость первого туриста 6 км/ч, скорость второго туриста 4 км/ч

Приложение 4

Домашняя работа.

№478

Фермер отправился на машине в город, находящийся на расстоянии 110 км от фермы. Через 20 мин из города на ферму выехал его сын, который проезжал в час на 5 км больше. Встреча произошла в 50 км от города. С какой скоростью ехал фермер?

Ответ: 45 км/ч скорость фермера.

№494

Расстояние в 360 км легковой автомобиль прошел на 2 ч быстрее, чем грузовой. Если скорость каждого автомобиля увеличить на 30 км/ч, то грузовой затратит на весь путь на 1 ч больше, чем легковой. Найдите скорость каждого автомобиля.

Ответ: 90 км/ч скорость легкового автомобиля, 60 км/ч скорость грузового автомобиля

№495

Бассейн наполнится. Если первую трубу открыть на 12 мин, а вторую – на 7 мин. Если же обе трубы открыть на 6 мин. То наполнится 2/3 бассейна. За сколько минут наполнится бассейн, если открыть только вторую трубу?

Ответ: за 15 мин вторая труба заполнит весь бассейн.

Ссылки:

-Задача магического квадрата для более успевающих учащихся.

http://nrich.maths.org/1887

- Видео для самостоятельной подготовки:

https://www.youtube.com/watch?v=BDvWXb-lMU0

Скачано с www.znanio.ru