10.Методические рекомендации к проведению урока. Вариант 2

Методические рекомендации к проведению урока

Цель обучения: 6.2.2.19 решать системы уравнений способом подстановки и способом сложения;

Критерии оценивания:

- определяет решение линейного уравнения с двумя переменными

- решает системы уравнений способом подстановки и способом сложения;

Организационный момент. Приветствие. Отметка отсутствующих. Проверка готовности учащихся к уроку.Совместно с учащимися определяем цели урока и ожидаемые результаты. Разбор домашнего задания.

Предложите учащимся повторить пройденный материал с помощью приема «Мяч вопросов и ответов». Учитель бросает мяч, когда задает вопрос. Это делает процесс опроса кинестетическим и позволяет вовлечь учеников, обычно не проявляющих желание отвечать добровольно. Вы можете позволить ученикам перебросить вопрос кому-то другому в случае, если они не знают ответа. Данное задание можно также выполнять в командах. Учитель по очереди кидает мяч каждой команде. Если ученик, поймавший мяч, отвечает на вопрос – его команда зарабатывает 3 балла. Если же он не знает ответа, то перебрасывает мяч другой команде за 2 балла.  В случае если мяч перебрасывается еще раз, стоимость правильного ответа снижается до 1 балла.

Примерный перечень вопросов:

1.             Какое уравнение называется линейным уравнением   с двумя переменными?

2.      Что называется решением линейного уравнения с двумя переменными?

3.      Когда говорят, что заданные уравнения образуют систему уравнений?

4.      Какие вы знаете способы решения систем уравнений?

5.      Как называется способ решения системы уравнений, при котором сначала выражают одну переменную через другую, а затем подставляют полученное выражение вместо другой переменной?

Вызов. Предложите учащимся рассмотреть еще один способ решения систем линейных уравнении – способ сложения.  Напомните учащимся, что при решении этим способом, как и при решении способом подстановки, делается переход от данной системы к другой, равносильной ей системы, в которой одно из уравнении содержит только одну переменную. Вместе с учащимися рассмотрите решение системы уравнении способом сложения.

(1)

В уравнениях этой системы коэффициенты при у являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной:

Заменим одно из уравнении системы (1), например первое, уравнением . Получим систему:

(2)

Система (2) равносильна системе (1). Решим систему (2). Из уравнения  находим, что  

Подставив это значение х в уравнение

Получим уравнение с переменной у:

Решим это уравнение:

Находим х:

Пара чисел ) – решение системы (2), а значит, и данной системы (1).

   Совместно с учащимися составьте алгоритм решения системы уравнений с двумя переменными методом алгебраического сложения:

1.Преобразовать уравнения системы так, чтобы в результате сложения получилось уравнение с одной переменной (если необходимо).
2.Сложить отдельно левые и правые части уравнений системы.
3.Решить уравнение с одной переменной.
4.Найденное значение переменной подставить в любое уравнение и найти значение второй переменной.

Предложите учащимся фронтальная работа. Ученики выполняют задания в парах, обучают друг друга, работают в «зоне ближайшего развития». Несколько учеников работают у доски. Учитель оказывает поддержку ученикам по мере необходимости. Ценность: умение работать в сотрудничестве. Проверяем результаты, какие получили ответы? Установление правильности и осознанности изучения темы.

Пример 1. Решить систему уравнений:

Умножим обе части первого уравнения на  

Получим:

Заметим, что уравнения содержат слагаемые . Теперь уже можно воспользоваться методом сложения:

Подставим найденное значение   в первое уравнение:

Получаем решение:

Ответ

 Пример 2. Решить систему уравнений:

Преобразуем уравнения системы так, чтобы в результате сложения получилось уравнение с одной переменной:

Получим следующую систему:

Складываем уравнения:

Подставим найденное значение в первое уравнение системы:

Ответ:

Пример 3. Решить систему уравнений:

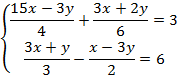
Упростим уравнения: избавимся от знаменателей:

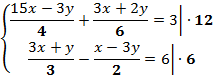
Тогда получим:

Раскроем скобки при помощи распределительного закона:

Приведем подобные слагаемые:

Преобразуем уравнения системы так, чтобы в результате сложения получилось уравнение с одной переменной:

Получаем:

Складываем уравнения:

<

Подставим найденное значение в первое уравнение системы:

Ответ: 

 Пример 4:

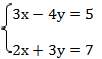
В данном случае если сразу применить метод алгебраического сложения, это ничего не даст и ни одна из переменных не уничтожится, так как ни одна из переменных не имеет противоположных коэффициентов, чтобы можно было применить данный метод, произведем некоторые преобразования:

Получаем:

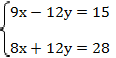
 Теперь противоположные коэффициенты имеет переменная у, и при сложении уравнений переменная уничтожится:

Подставим значение х во второе уравнение и найдем у:

Ответ: (             

Обратим внимание на то, что мы рассматриваем метод алгебраического сложения, значит, уравнения можно не только складывать, но и вычитать. Рассмотрим пример:

Пример 5:

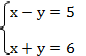
При сложении уравнений получим:

, 

Попробуем вычесть уравнения, причем, вычтем первое из второго:

, 

Пример 4:

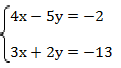
Хотелось бы сложить уравнения, чтобы избавиться, например, от переменной х, но для этого исходные уравнения необходимо преобразовать:

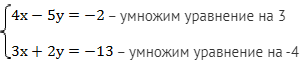
Получаем:

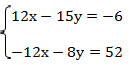
Выполним сложение, получим:

Подставим полученное значение у в первое уравнение:

Ответ: (-3; -2)

Дескриптор:

- выбирает способ решения системы уравнений;

- выполняет алгебраические преобразования уравнений;

-находит значение переменной х;

- находит значение переменной у;

-записывает решение системы уравнений

Предложите учащимся провести физкультминутку.

Для закрепления пройденной тему предложите учащимся прием Посол.

Цель: Активное слушание, публичное выступление и ясность изложения, разделение и создание взаимозависимости.

Организация: Разместите группы по 3-4 человека в классе и предложите карточки с заданиями по теме.

Как это работает: Когда группа выполнила задание, один ученик из каждой группы выбирается «представителем» и перемещается к другой группе, чтобы объяснить и обобщить, и выяснить идеи другой группы.  Затем представитель возвращается в свою группу, чтобы сообщить, что он узнал.

Ответ: 1. (2.

Дескриптор:

- выбирает способ решения системы уравнений;

- выполняет алгебраические преобразования уравнений;

-находит значение переменной х;

- находит значение переменной у;

-записывает решение системы уравнений

Рефлексия.

Подведение итогов урока.

Домашнее задание: № 1535 стр.370

Ресурсы:

1.Методическое руководство «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова.

2.Учебник «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова. Алматы. Атамура. 2011 год.