
6 класс
Тема. Прямая и обратная пропорциональность. Дата______________
Цель. Проверить знания учащихся по теме «Пропорции». Закрепить определение прямо пропорциональных и обратно пропорциональных величин. Научится решать задачи по данной теме.
Ход урока.
I. Организационный момент.
II. Проверка домашнего задания.
III. закрепление нового материала.
Прямая и обратная пропорциональность.
(Пусть ручка стоит 3 р. (это цена).
Тогда легко рассчитать стоимость двух, трех и т.д. ручек по формуле: ![]() .
.
|
Количество ручек, шт. |
1 |
2 |
3 |
4 |
|
Стоимость, р. |
3 |
6 |
9 |
12 |
Заметим, что с увеличением количества ручек в несколько раз их стоимость увеличивается во столько же раз.
Говорят, что стоимость покупки прямо пропорциональна количеству купленных ручек.
Определение. Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональных величин:
1. Периметр квадрата
и длина стороны квадрата – прямо пропорциональные величины. ![]() .
.
2. Если скорость
движения постоянна, то пройденный путь и время движения – прямо
пропорциональные величины. ![]() .
.
3. Если
производительность труда постоянна, то объём выполненных работ и время – прямо
пропорциональные величины. ![]() .
.
4. Выручка кассы кинотеатра прямо пропорциональна количеству проданных билетов при одинаковой цене. И т.д.
Задача 1. За 5 тетрадей в клетку заплатили 40 р. Сколько заплатят за 12 таких же тетрадей?
Кол-во Стоимость
![]()
![]() 5 тетрадей – 40 р. Прямая пропорциональность
5 тетрадей – 40 р. Прямая пропорциональность
12 тетрадей – х р.
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
![]() ,
,
![]() ,
,
![]() .
.
96 р. заплатят за 12 тетрадей. Ответ: 96 р.
Хотят купить на 120 р. несколько
одинаковых книг. Тогда легко рассчитать количество книг по 10 р., 20 р., 30 р.
40 р. и т.д. по формуле: 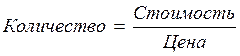 .
.
|
Цена, р. |
10 |
20 |
30 |
40 |
|
Количество книг, шт. |
12 |
6 |
4 |
3 |
Заметим, что с увеличением цены книги в несколько раз их количество уменьшается во столько же раз.
Говорят, что количество купленных книг обратно пропорционально их цене.
Определение. Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению значений другой величины.
Примеры обратно пропорциональных величин:
1. Если пройденный
путь постоянен, то скорость движения и время движения – обратно
пропорциональные величины. 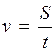 .
.
2. Если
производительность труда постоянна, то объём выполненных работ и время –
обратно пропорциональные величины. 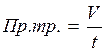 .
.
Задача 2. 6 рабочих выполнят работу за 5 часов. За какое время справятся с этой работой 3 рабочих?
![]() Кол-во Время
Кол-во Время
![]() 6 рабочих – 5 ч Обратная пропорциональность
6 рабочих – 5 ч Обратная пропорциональность
3 рабочих – х ч
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
![]() ,
,
![]() ,
,
![]() .
.
За 10 ч справятся с этой работой 3 рабочих. Ответ: 10 ч.
Алгоритм решения задач.
1. Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом)
2. Составить пропорцию.
v Если две величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
v Если две величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
3. Найти неизвестный член пропорции.
4. Проанализировать полученный результат и записать ответ.
IV. Решение упражнений.
Уч.с.21 № 75(а). В 100 г раствора содержится 4 г соли. Сколько соли содержится в 300 г этого раствора?
![]()
![]() Р-р
Соль
Р-р
Соль
100 г – 4 г Прямая пропорциональность
300 г – х г
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
![]() ,
,
![]() ,
,
![]() .
.
12 г соли содержится в 300 г этого раствора. Ответ: 12 г.
Уч.с.22 № 88. Некоторую работу 6 человек сделают за 18 дней. За сколько дней сделают эту же работу 9 человек, работающие так же успешно, как и первые?
![]() Кол-во Время
Кол-во Время
![]() 6 человек – 18 дн. Обратная пропорциональность
6 человек – 18 дн. Обратная пропорциональность
9 человек – х дн.
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
![]() ,
,
![]() ,
,
![]() .
.
За 12 дней сделают эту же работу 9 человек. Ответ: 12 дней.
Уч.с.22 № 83. Один килограмм
металлолома заменяет ![]() кг богатой железом руды.
Сколько руды заменяют 4 т металлолома?
кг богатой железом руды.
Сколько руды заменяют 4 т металлолома?
Металлолом Руда
![]()
![]() 1 кг –
1 кг – ![]() кг Прямая пропорциональность
кг Прямая пропорциональность
4 т – х кг
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
1) 4 т = 4000 кг;
2) 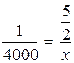 ,
,
![]() ,
,
![]() .
.
10 000 кг руды заменяют 4 т металлолома. Ответ: 10 000 кг.
Уч.с.22 № 84(а). Автомобилист заметил, что со скоростью 60 км/ч он проехал мост через реку за 40 с. На обратном пути он проехал этот же мост за 30 с. Определите скорость автомобиля на обратном пути?
![]() v t
v t
![]() 60 км/ч – 40 с Обратная пропорциональность
60 км/ч – 40 с Обратная пропорциональность
х км/ч – 30 с
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
![]() ,
,
![]() ,
, ![]() .
.
80 км/ч скорость автомобиля на обратном пути. Ответ: 80 км/ч.
V. Подведение итогов урока
VI. Домашнее задание. § 1.5 (выучить теорию). № 75(б), 77(а), 84(б).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.