15.Методические рекомендации к проведению урока. Вариант 2

Методические рекомендации к проведению урока

Цель обучения: 6.2.2.15 изображать множества точек на координатной прямой, заданные неравенствами вида

;

Критерии оценивания:

-выполняет действия с неравенствами;

-изображает на координатной прямой пересечение и объединение числовых промежутков;

-записывает решения неравенств в виде числового промежутка и записывает числовой промежуток в виде неравенства;

-изображает множества точек на координатной прямой, заданные неравенствами вида ;

Организационный момент.     

Для того чтобы перейти к изучению нового материала, необходимо вспомнить ранее изученный материал.

Актуализация учебных знаний.

Предложите учащимся повторить темы: модуль числа, линейное уравнение, правила решения линейного уравнения.

Вопросы по методике Блума на ромашке:

 (1 ответ – 1 «+»)

1) Что такое модуль?

2) Как Вы думаете, равны ли модули чисел -5 и 5? Почему?

3) Вычислите;  ;  

4)  Может ли модуль быть отрицательным числом?

 5) Чему равен x , если   ;       ?

 6)  Сколько значений имеет х, если модуль его равен положительному числу? Отрицательному числу и равен 0?

Прием: «Горячий стул». (1 ученик садится на стул посередине и отвечает на вопросы класса. 1 ответ – один «+») 

Например:

1.Какое уравнение называется линейным?

2.Обе части уравнения умножили на число, не равное 0. 3.Изменились ли корни данного уравнения?

4.Обе части уравнения разделили на одно и то же число, отличное от нуля. Изменились ли корни данного уравнения?

5.Сформулируйте правило переноса слагаемых из одной части уравнения в другую.

Изучение новой темы:

Модуль числа а обозначается .

Модуль положительного числа равен самому числу.

Например:|3|= 3; ||=;  |2,4|= 2,4

Модуль отрицательного числа равен противоположному ему числу.

Например: |-2| = -(-2) = 2;  |-|= -(-)= 

Пример: |х-1|+ х < 5-|2х-5|.

 Модуль нуля равен нулю: |0|= 0.

Определение модуля числа можно записать в виде:

Рассмотрим геометрический смысл модуля числа.

Изобразим на числовой прямой, например, точки 3 и -2.

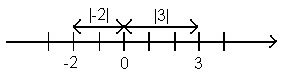Из рисунка видно, что |3|=3 есть расстояние в единичных отрезках от точки 0 до точки 3; а |-2|=2 есть расстояние в единичных отрезках от точки 0 до точки -2.

Итак, геометрическиесть расстояние в единичных отрезках от точки 0 до точки, изображающей число а.

  Рассмотрите с учащимися несколько примеров на решение

Тренировочные упражнения. Организуйте фронтальную работу по  решению линейных неравенство с одной переменной, содержащее переменную под знаком модуля у доски. Учащиеся по желанию выходят к доске, оформляют решение на доске, делают комментарии, остальные учащиеся сверяют свои ответы.

Задание 1. Изобразите на числовой прямой множество решений неравенства:

1)                 2)                       3)                          4)

Задание 2. Запишите неравенство с модулем в виде двойного неравенства:

1)                 2)                      

Решение: ; 2)

Задание 3. Двойное неравенство запишите в виде одного неравенства с модулем:

1)          2)       

Решение:

Дескриптор:

-выполняет действия с неравенствами;

-изображает на координатной прямой пересечение и объединение числовых промежутков;

-записывает решения неравенств в виде числового промежутка и записывает числовой промежуток в виде неравенства;

-находит решение системы неравенств.

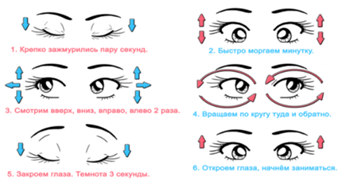
Проведите гимнастику для глаз.

Для закрепления пройденной тему предложите учащимся прием Посол.

Цель: Активное слушание, публичное выступление и ясность изложения, разделение и создание взаимозависимости.

Организация: Разместить группы по 3-4 человека в классе.

Как это работает: Когда группа выполнила задание, один ученик из каждой группы выбирается «представителем» и перемещается к другой группе, чтобы объяснить и обобщить, и выяснить идеи другой группы.  Затем представитель возвращается в свою группу, чтобы сообщить, что он узнал. Это эффективный метод избегания скучного и повторяющегося «сообщения своей группе». Это также способствует использованию языка представителя и создает группу активных слушателей.

Решите неравенство, пользуясь определением модуля:

Решение:

Дескриптор:

-выполняет действия с неравенствами;

-изображает на координатной прямой пересечение и объединение числовых промежутков;

-записывает решения неравенств в виде числового промежутка и записывает числовой промежуток в виде неравенства;

-находит решение системы неравенств.

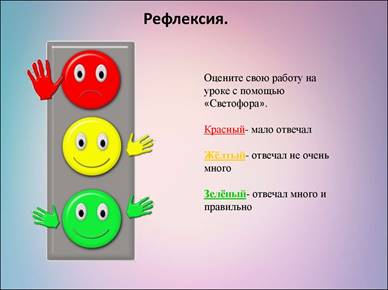
Рефлексия.

Подведение итогов урока. Рефлексия.

Учащиеся выполняют саморефлексию, отвечая на вопросы:

- что узнал, чему научился?

- что осталось непонятным?

-над чем необходимо работать?

Домашняя работа.

Ресурсы:

1.Методическое руководство «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова.

2.Учебник «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова. Алматы. Атамура. 2011 год.