16.Методические рекомендации к проведению урока. Вариант 2

Методические рекомендации к проведению урока

Цель обучения: 6.2.2.15 изображать множества точек на координатной прямой, заданные неравенствами вида

;

Критерии оценивания:

-выполняет действия с неравенствами;

-изображает на координатной прямой пересечение и объединение числовых промежутков;

-записывает решения неравенств в виде числового промежутка и записывает числовой промежуток в виде неравенства;

-изображает множества точек на координатной прямой, заданные неравенствами вида ;

Организационный момент. Актуализации знаний, умений, навыков.

 Предложите учащимся Математический диктант.

 Продолжить определения:

    а) Решить систему линейных неравенств – значит найти все её решения или доказать, что их нет.

    б) Решением системы неравенств с одной переменной  называется значение переменной, при котором верно каждое из неравенств.

    в) Чтобы решить систему неравенств с одной переменной нужно найти решение каждого неравенства, и найти пересечение этих промежутков.

     Напомните учащимся о том, что умение решать линейные неравенства с одной переменной и их систем является основой, базой для более сложных неравенств, которые предстоит изучить в более старших классах. Закладывается фундамент знаний, прочность которого предстоит подтвердить на МЭСК по математике после 10 класса.

  Ученики письменно в тетради решают системы линейных неравенств с одной переменной.           (2 ученика выполняют эти задания на доске, поясняют свое решение, озвучивают свойства неравенств, использованные при решении систем).

Задание №1.Решите систему линейных неравенств:

Ответ. ( 30; +∞ ).

Задание №2. Решите двойное неравенство и укажите все целые числа, которые являются его решением

Ответ. Целое число: 0

Задание №3.Решить неравенства:

а) .

 Ответ

б)|. 

 Ответ.

        Предложите учащимся продолжить в группах сменного состава. Каждая группа получает список заданий, который надо выполнить.

Основная цель: «Все члены группы должны знать решение всех задач и могут продемонстрировать решение любого из них.» Поэтому каждый ученик выбирает себе задание. Выполняет её полное решение с описанием и комментариями. Если он испытывает трудности или сомневается при решении выбранной задачи, он объединяется в группу нового состава, в которую собираются все участники других групп, решающие эту задачу. Выполняет запись решения. Затем все учащиеся снова собираются в группу исходного состава и осуществляют взаимообучение.

Дескриптор:

-выполняет действия с неравенствами;

-изображает на координатной прямой пересечение и объединение числовых промежутков;

-записывает решения неравенств в виде числового промежутка и записывает числовой промежуток в виде неравенства;

-находит решение системы неравенств.

Закрепление темы с помощью приема «Автобусная остановка».

Цель: Принимать во внимание чужие идеи, целостно обсудить тему или вопрос, активно и пассивно.

Организация: Серии станций в комнате с бумагой и ручкой (или раздайте группе разноцветные карандаши – поэтому нужно следить кто что нарисовал)

Как это работает: Разместите каждую малую группу на станции, дайте 3-4 минут обсудить задание и записать их мысли на бумаге или доске. По истечению времени, группа перемещается к другой станции, где группа продолжает работу предыдущей группы. Перемещение происходит каждые минут, пока каждая группа не побывала на каждой позиции и обдумала мысли всех групп.

Остановка №1. «Линейное уравнение с одной переменной».

Ответ

Остановка №2. Линейное уравнение с одной переменной, содержащее переменную под знаком модуля.

Ответ:

Остановка №3. Решение текстовых задач с помощью уравнении.

Расстояние от пункта А до пункта В теплоход проплыл против течения за 1 час 48 мин. На обратный путь от пункта В до пункта А он затратил на 18 мин меньше. Скорость течения реки 2,4 км/ч. Найдите собственную скорость теплохода.

Ответ: 26,4 км/ч

Остановка №4. Линейное неравенство с одной переменной.

Ответ:

Остановка №5. Системы линейных неравенств с одной переменной.

Ответ:

Остановка №6. Линейное неравенство с одной переменной, содержащее переменную под знаком модуля.

Ответ:

Дескриптор:

-выполняет действия с неравенствами;

-изображает на координатной прямой пересечение и объединение числовых промежутков;

-записывает решения неравенств в виде числового промежутка и записывает числовой промежуток в виде неравенства;

-находит решение системы неравенств.

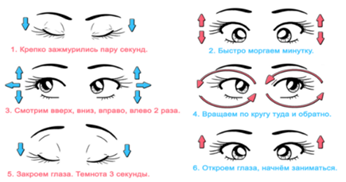
Проведите гимнастику для глаз.

Рефлексия.

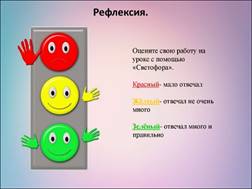
Подведение итогов урока. Рефлексия.

Учащиеся выполняют саморефлексию, отвечая на вопросы:

- что узнал, чему научился?

- что осталось непонятным?

-над чем необходимо работать?

Домашняя работа.

Ресурсы:

1.Методическое руководство «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова.

2.Учебник «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова. Алматы. Атамура. 2011 год.