18. Методические рек Вариант 1

Методические рекомендации к проведению урока

      Начните урок с выполнения с учащимися упражнение на воспитание уверенности в себе и самоуважению. «Дружеская мойка». Учитель расставляет детей на небольшом расстоянии в два параллельных ряда лицом друг к другу. Один ученик проходит между этими рядами («через мойку»). Каждый дружески похлопывает его по спине или пожимает руку, одновременно произнося слова похвалы, симпатии и поощрения. В результате такой «мойки» появляется сияющий, радостный и счастливый ребёнок. Затем он встаёт в свой ряд, и процедура повторяется. (2-3 раза).

  Разбор домашнего задания. Учащиеся обмениваются домашним заданием и выполняют проверку по готовым решениям.

 Предложите учащимся фронтальную работу. Ученики выполняют задания в парах, обучают друг друга, работают в «зоне ближайшего развития». Учитель оказывает поддержку ученикам по мере необходимости. Ценность: умение работать в сотрудничестве

Задача: Разделить число 100 на две части прямо пропорционально числам 2 и 3.

Решение:

Эту задачу следует понимать так: разделить 100 на две части, чтобы первая относилась ко второй, как 2 и 3. Если обозначить искомые числа буквами х₁ и х₂, то эту задачу можно сформулировать и так. Найти х₁и х₂ такие, чтобы

х₁ + х₂ = 100,

х₁ : х₂ = 2 : 3.

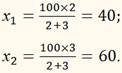
ОТВЕТ: 40 и 60.

Задача Разделить 780 на четыре части пропорционально числам 1,5, 0,75, 0,4, 1,25.

Решение. Эту задачу следует понимать так: если обозначить искомые числа через х₁, х₂, х₃ и х₄, то:

Умножив каждый из знаменателей на 100 и воспользовавшись свойством равных отношений, получим:

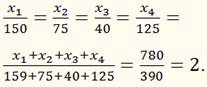
Откуда:

х₁ = 300, х₂ = 150,

х₃ = 80, х₄ = 250. 

 Предложите учащимся, сидящим «на I варианте» разделить число 144 в отношении, а учащихся сидящих «на II варианте» в отношении.Сравните условия данных задач и задачи:

Разделите число 144 обратно пропорционально числам 3 и 5 (или 7 и 5).

         Предложите учащимся в парах составить алгоритм решения задач на деление в обратно пропорциональном отношении.

Предложите учащимся самостоятельно решить задачи:

1.      Отрезок длиной 1 м разделили на две части, длины которых обратно пропорциональны числам 2 и 3. Найдите длины этих отрезков.

Решение:

1) Число 1 разделим на части, обратно пропорциональные числам 2 и 3

 : = 3 : 2

3+ 2 = 5

1 : 5  3 =

1 : 5  2 =

2.      Число 88 разделите на три части обратно пропорционально числам 2:;.

Числа, обратные данным:

Следовательно,

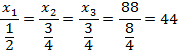
Ответ: 22,33,33

3. Разделите число 144 на три части х, у, z так, чтобы

 x: у = 3:4, у: z = 4:5.

Решение:

х: y:z=3:4:5
Значит, всего 3+4+5=12 частей.
Каждая часть равна 144:12=12.
Следовательно,

36:48=3:4, 48:60=4:5
Проверим:
36+48+60=144.

3.      Три числа относятся, как 3:5:8, третье число равно 112. Вычислите два первых числа.

Решение:

Дифференциация выражена в виде заданий, требующих разного уровня математической подготовленности, а так же с учетом скорости мышления и возрастных особенностей учащихся.

              Предложите учащимся групповую работу.

 На данном этапе урока у учащихся развивается умение сотрудничать с одноклассниками и учителем при совместной работе, умение прислушиваться к мнению других. Учитель делит учащихся на группы по уровню усвоения знаний (базовый, продвинутый). Каждая группа получает задания. Решая задания, учащиеся закрепляют понятие деления величины на части, обратно пропорциональные данным числам.

Базовый уровень:

 1) Число 91 разделим на части, обратно пропорциональные числам 5 и 8

2) число 143 разделите на части, обратно пропрорциональные числам 4 и 7

3) Число 27 разделить обратно пропорционально числам 4 и 5.

Продвинутый уровень:

4) число 104 разделите на части, обратно пропрорциональные числам 2,3,4

5) Разделить число 52 на три части обратно пропорционально числам 4, 6 и 8.

 Каждый из учеников работает в «зоне ближайшего развития» и получает поддержку от одноклассников и учителя. После выполнения заданий, учащиеся проводят взаимопроверку правильности выполнения заданий по образцу, выданному учителем. Если в классе несколько одинаковых групп по уровням усвоения, то можно провести взаимопроверку групп.

Решение:

1) Число 91 разделим на части, обратно пропорциональные числам 5 и 8

1/5 : 1/8 = 8 : 5

8+5 = 13

91 :13 * 8 = 56

91 : 13 * 5 = 35

2) число 143 разделите на части, обратно пропрорциональные числам 4 и 7

1/4 : 1/7 = 7 : 4

7+4 = 11

143 : 11 * 7 = 91

143 : 11 * 4 = 52

3) число 104 разделите на части, обратно пропорциональные числам 2,3,4.

Обратные числа - 1/2; 1/3 и 1/4

Приведем их к общему знаменателю = 6/12: 4/12 : 3/12, затем уберем его и сложим числители

6 + 4 + 3 = 13

а теперь число 104 делим на 13 и умножаем по-порядку на числители 6, 4 и 3

104 : 13 * 6 = 48
104 : 13 * 4 = 32
104 : 13 * 3 = 24

4) Разделить число 52 на три части обратно пропорционально числам 4, 6 и 8.

Решение:

Числа, обратные данным:

¹/₄, ¹/₆ и ¹/₈.

Следовательно,

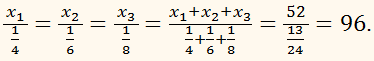
х₁ = ¹/₄ 96 = 24,

х₂ = ¹/₆  96 = 16,

х₃ = ¹/₈  96 = 12.

Ответ:24, 16 и 12.

 5) Число 27 разделить обратно пропорционально числам 4 и 5.
Решение: Числа, обратные данным, относятся как  

Получим 27:9·5=15; 27:9·4=12

Предложите учащимся самостоятельную работу для формативного оценивания.

 (базового или продвинутого уровня).

Выполняя самостоятельную работу у учашихся разиваются такие ценности как упорство в достижении цели, трудолюбие.

В конце урока учащиеся проводят рефлексию:

- что узнал, чему научился

- что осталось непонятным

- над чем необходимо работать

Учащиеся на листках записывают свои выводы.

Ресурсы:

Алдамуратова Т.А. «Атамұра»2015 г.

Стр 59–60, задачи №1–4

http://edu.alnam.ru/book_kram.php?id=26

http://krasavtsev.blogspot.com/2016/02/arifmetika35.html

Скачано с www.znanio.ru