
Методические рекомендации к уроку
Тема урока "Решение линейных неравенств с одной переменной, содержащих переменную под знаком модуля"
Цели обучения:
6.2.2.15 изображать множество точек на координатной прямой, заданное неравенством вида |x| > a, |x| ≥ a, |x| < a, |x| ≤ a.
Критерии оценивания:
Учащиеся
знают:
□
как изображать множество точек на координатной прямой, заданное
неравенством вида
|x| > a, |x| ≥ a, |x| < a, |x| ≤ a;
□ как записывать, используя математическую символику, ответы к решению неравенства;
умеют
□ изображать
множество точек на координатной прямой, заданное неравенством вида
|x| > a, |x| ≥ a, |x| < a, |x| ≤ a;
□ использовать обозначения для записи числовых промежутков в ответах;
записывать решения систем неравенств в виде числового промежутка и записывать заданный числовой промежуток в виде неравенства.
Теоретический материал
Несколько неравенств с одной переменной образуют совокупность неравенств, если нужно найти все такие значения переменной, каждое из которых является решением хотя бы одного из заданных неравенств.
Каждое такое значение переменной называют частным решением совокупности неравенств.
Множество всех частных решений совокупности неравенств представляет собой решение совокупности неравенств.
Решение совокупности неравенств представляет собой объединение решений неравенств, образующих совокупность.
Неравенства, образующие совокупность, объединяются квадратной скобкой.
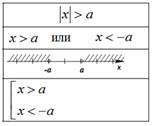
Решение неравенства![]() равносильно решению
неравенства:
равносильно решению
неравенства: ![]() , можно записать в виде
совокупности:
, можно записать в виде
совокупности:
Ход урока
Организационный момент.
Проверить домашнее задание.
Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".
Актуализация опорных знаний. Устный опрос.
1.
Что является решением неравенства ![]()
2. Что
является решением неравенства ![]()
3. В каком случае неравенство с модулем имеет бесконечное множество решений?
4. Приведите примеры неравенства, не имеющие решений.
Предложите учащимся письменно решить несколько неравенств с модулем, постепенно усложняя задание.
Приложение 1
Задание 1. Имеет ли решение неравенство:
а) ![]() б)
б) ![]() в)
в) ![]()
г) ![]() д)
д) ![]() е)
е) ![]() ?
?
Задание 2. Запишите в виде двойного неравенства неравенство с модулем:
а) ![]() ; б)
; б) ![]() в)
в) ![]()
Задание 3. Запишите в виде неравенства с модулем двойное неравенство:
а) ![]() б)
б) ![]() в)
в) ![]()
Решить неравенство, изобразить геометрически решение, записать в виде числового промежутка:
Задание 4.а) ![]() б)
б) ![]()
|
-45 < 15x < 45 |
15x < -45 или 15x>45 |
|
-3 < x < 3 |
x < -3 или x>3 |
![]()
![]()
Ответ: ![]() Ответ:
Ответ: ![]()
Задание 5. а) ![]() б)
б) ![]()
|
- 84 < - 28x < 84 |
28x < -84 или 28x>84 |
|
- 3< x < 3 |
x < -3 или x>3 |
![]()
![]()
Ответ: ![]() Ответ:
Ответ: ![]()
Задание 6. а) ![]() б)
б)![]()
|
|
|
|
-11 < 11x < 11 |
11x < -11 или 11x>11 |
|
-1 < x < 1 |
x < -1 или x>1 |
![]()
![]()
Ответ: ![]() Ответ:
Ответ: ![]()
После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать задания, которые были сделаны с ошибками.
Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями. Чтобы закрепить решение неравенств используем метод Джигсо (в группе разбирают решение неравенств, затем 1 представитель группы пересаживается в другую группу и объясняет, как решается неравенство и так в каждой группе).
Приложение 2.
Задание 1. Решите неравенство:
а) ![]() б)
б) ![]() в)
в) ![]()
Задание 2. Решите неравенство и запишите множество его целых решений:
а)![]() б)
б) ![]() в)
в) ![]()
Задание 3. Решите двойное неравенство и запишите множество его целых решений:
а) ![]() б)
б) ![]() в)
в) ![]()
Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.
Предоставить учащимся достаточно времени для выполнения заданий.
Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения заданий.
Старший группы оценивает вклад каждого, выставляя отметку.
Индивидуальная работа. Формативное оценивание. Для закрепления и оценки усвоения пройденного материала предложить учащимся задания из учебного пособия уровня В, аналогичные заданиям, решенным при групповой работе. Количество заданий, обязательных для решения на усмотрение учителя в зависимости от обучаемости класса.
После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать задания, которые были сделаны с ошибками.
Провести формативное оценивание «Сигналы рукой»:
Кому всё понятно?
Кому не совсем понятно? Что именно?
Кто вообще не понял? Что именно не понял?
Обобщить информацию.
Приложение 3. Заполнить таблицу.
|
1. |
|f(x)| < a |
a£0 |
нет решений |
|
2. |
|f(x)| < a |
a > 0 |
-a < f(x) < a |
|
3. |
|f(x)|£ a |
a < 0 |
нет решений |
|
4. |
|f(x)|£ a |
a = 0 |
f(x) = 0 |
|
5. |
|f(x)|£ a |
a > 0 |
-a£ f(x) £a |
|
6. |
|f(x)| > a |
a < 0 |
Множество решений совпадает с решением f(x)>0 |
|
7. |
|f(x)| > a |
a = 0 |
f(x) ¹ 0 |
|
8. |
|f(x)| > a |
a > 0 |
f(x) < -a или f(x) > a |
|
9. |
|f(x)|³a |
a £0 |
множество решений совпадает с решением f(x)³0 |
|
10. |
|f(x)|³ a |
a > 0 |
f(x) £ -a или f(x)³0 |
|
|
Задания |
Достаточные знания |
Формулы |
|
1 |
∣x−2∣
≥8 ⇔ [ |
Равносильность неравенства с модулем |x|≥a, a>0 |
|x|≥a, a>0⇔[ |
|
2 |
∣x−2∣≥−8⇔x∈(−∞;+∞) |
Равносильность неравенства с модулем |x|≥a, a<0 |
|x|≥a, a<0⇔x∈(−∞;+∞) |
|
3 |
|2x−7|≤3⇔−3≤2x−7≤3 |
Равносильность неравенства с модулем |x|≤a, a>0 |
|x|≤a, a>0⇔−a≤x≤a |
|
4 |
|2x−3|≤−1⇔x∈∅ |
Равносильность неравенства с модулем |x|≤a, a<0 |
|x|≤a, a<0⇔x∈∅ |
|
5 |
x|2x−3|<2⇔ |
Определение модуля |a| |
|a|= |
Домашнее задание. Обязательное домашнее задание по цели обучения 6.2.2.15 по теме: «Решение линейных неравенств с одной переменной, содержащих переменную под знаком модуля» предполагает количество заданий, на выполнение которых учащиеся должны затрачивать не более 15-20 минут. Задания должны быть направлены на отработку навыков решения линейных неравенств с одной переменной, содержащих переменную под знаком модуля. Особое внимание уделить изображению решения неравенства на координатной прямой. Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.
Рефлексия.
В конце урока учащиеся проводят рефлексию, прикрепляя стикер со своим именем на слайде и или на бумаге, прикрепленной к доске, на смайлике, соответствующий его мнению.

На уроке предусмотрена дифференциация в виде работы в разнородных парах На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).
Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.
Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.
Литература:
1. "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;
2. "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.
3. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192
4. Вассерман Ф.Я. Математика 6 Учебное пособие для учащихся, изд БИС
Интернет ресурсы:
Интернет ресурсы:
1. http://www.yaklass.ru
2. https://school-assistant.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.