19. Системы линейных уравнений с двумя переменными. Метод

Методические рекомендации к уроку

Тема урока "Системы линейных уравнений с двумя переменными"

Цели обучения:

6.2.2.17

иметь представление о системах линейных уравнений с двумя переменными;

6.2.2.18

понимать, что решением системы линейных уравнений с двумя переменными является упорядоченная пара чисел;

Критерии оценивания

Учащиеся

знают:

·         что такое системы линейных уравнений с двумя переменными;

·         что является решением системы линейных уравнений с двумя переменными;

умеют

·         определять  решения системы линейных уравнений с двумя переменными и делают правильный выбор из упорядоченной пары чисел;

Теоретический материал

Определение. Если нужно найти общие решения двух уравнений (с двумя переменными), то говорят, что эти уравнения образуют систему уравнений.

Определение. Решением системы уравнений с двумя переменными называется (упорядоченная) пара значений переменных, при которых каждое уравнение системы превращается в верное числовое равенство.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Вопросы на повторение: Приложение 1

1.      Какие уравнения с двумя переменными называются линейными?

2.      Что является графиком линейного уравнения с двумя переменными?

3.      Из уравнения 3х-5у=7 выразить каждую переменную через другую.

4.      Что называется решением системы  линейных уравнений с двумя переменными?

5.      Что значит решить уравнение с двумя переменными?

6.      В чем достоинство и недостаток графического способа решения систем  линейных уравнений с двумя   неизвестными?

7.      Сформулировать алгоритм решения систем  линейных уравнений с двумя неизвестными графическим способом.

8.      Выразить у через x:

3x + y = 4               (y = 4 – 3x)
5x – y = 2               (y = 5x – 2)
1/2y – x = 7            (y = 2x + 14)
2x + 1/3y – 1 = 0    (y = – 6x + 3)

9.      Решить уравнение:

5x + 2 = 0             (x = – 2/5)
4x – 3 = 0             (x = 3/4)
2 – 3x = 0             (x = 2/3)
1/3x + 4 = 0          (x = – 12)

10. Дана система уравнений: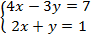 

Какая из пар чисел (– 1; 1) или (1; – 1) является решением данной системы уравнений?

Ответ: (1; – 1)

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Работа с классом. В режиме диалога провести исследование числа решений системы линейных уравнений с помощью графиков.

Графический способ особо удобен для определения количества решений системы уравнений, так как в этом случае важно только количество точек пересечения графиков, а не их координаты. Причем, если все уравнения системы – линейные, то количество ее решений можно определить и без построения графиков.

После повторения вопросов:

а) что является графиком линейного уравнения;

б) условие различных случаев взаимного расположения графиков двух линейных уравнений;

в) как из линейного уравнения выразить у через х учащимся можно предложить практические задания.

1. В каждом из уравнений системы 1) - 3) выразите у через х и, используя представления о свойствах взаимного расположения графиков двух линейных уравнений, определите (не выполняя построения), взаимное расположение графиков двух линейных уравнений:

1)                       2)             3)

 2. За взаимным расположением графиков определите количество решений системы.

3. Найдите отношение коэффициентов     (уравнений каждой системы) и сравните их между собой.

4. Сравните результаты выполнения п.3 c выводами п. 2. Сформулируйте вывод.

После выполнения и обсуждения результатов обобщаем и корректируем выводы и вносим соответствующие записи в тетради.

Приложение 2

 Устное решение системы уравнений “одним взглядом”

Сколько решений у системы?

Учащиеся формулируют выводы, сравнивают с текстом учебника, корректируют свои выводы.

Работа в парах. Взаимное обучение. Создать пары из представителей разных групп. Предложить ученикам процесс взаимного обучения: объяснить напарнику ход решения задания, затем вместе решить их. Определяем умение распределять обязанности в паре.

Приложение 3

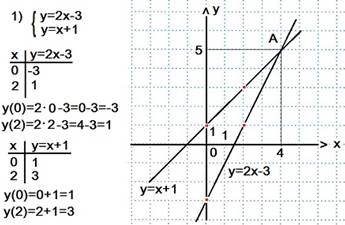
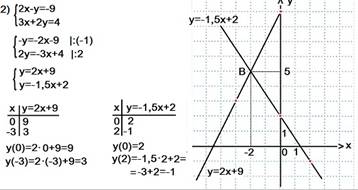
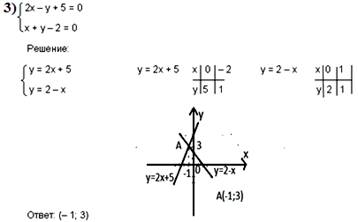
Подвести итог после решения этих заданий.

Пригласите к доске ученика, попросите его записать подробное решение задания. Учащиеся на местах решают все примеры и сверяют свои решения с записями на доске, внимательно слушают одноклассников. С целью развития математической речи попросите одного из учащихся подробно прокомментировать решение любого задания, акцентируйте их внимание на обоснование решений. Для учащихся с более высокой скоростью решения организуйте "уголок Знайки", куда они могли бы подходить и проверять свое решение или читать идею решения. Это позволяет не отвлекаться на объяснение задачи, а работать в это время с остальной частью класса.

При наличии компьютера, просмотреть презентацию для визуального закрепления материала.

Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями.

Приложение 4

Задание 1:

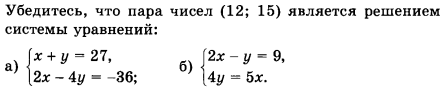
Задание 2:

Задание 3:

Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия.

В конце урока учащиеся проводят рефлексию, прикрепляя стикер со своим именем на слайде и или на бумаге, прикрепленной к доске.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1.                  "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2.                  "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3.                  Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4.                  Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

5.                  Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.

Интернет ресурсы:

1.                  http://www.yaklass.ru

2.                  https://school-assistant.ru

3.