
|
Раздел долгосрочного плана: 9.3В Решение текстовых задач |
Школа: ФИО учителя: |
|||||||
|
Дата: |
|
|||||||
|
Класс: 9 |
Количество присутствующих: |
отсутствующих: |
||||||
|
Тема урока |
Геометрическая вероятность |
|||||||
|
Цели обучения, которые достигаются на данном уроке |
9.3.2.5 применять геометрическую вероятность при решении задач; |
|||||||
|
Цели урока |
· Дальнейшая отработка умений применять геометрическую вероятность при решении задач. · Научить учащихся решать текстовые задачи “о встрече” с помощью геометрической вероятности. |
|||||||
|
Критерии оценивания |
· - знает и применяет понятие геометрической вероятности при решении задач; · -умеет различать задачи на применение геометрической вероятности; · -умеет решать задачи о встрече · - умеет анализировать условие задачи |
|||||||
|
Языковые цели |
Учащиеся будут: - обосновывать почему применяют формулу геометрической вероятности; - объяснять пути решения задач с помощью классической вероятности; Предметная лексика и терминология ⦁ случайное событие; ⦁ элементарное событие; ⦁ равновозможные; ⦁ достоверные; ⦁ невозможные; ⦁ благоприятствующие исходы; ⦁ всевозможные исходы; ⦁ вероятность; ⦁ абсолютная и относительная частота; ⦁ геометрическая вероятность; ⦁ геометрическая мера; ⦁внутренний отрезок, площадь, объем. Набор полезных фраз для общения/письма: - количество благоприятствующих исходов события ... . - найдем вероятность данного события; - вероятность попадания точки в данную область ...
|
|||||||
|
Межпредметные связи |
Экономика,физика |
|||||||
|
Навыки использования ИКТ |
Овладевать практическими навыками работы с информацией, развивать умения, позволяющие обмениваться с информацией. |
|||||||
|
Первоначальные знания |
-знание определения классической вероятности; -знание формулы геометрической вероятности; -знание формул площадей геометрических фигур. |
|||||||
|
План |
||||||||
|
Этапы урока |
Запланированная деятельность на уроке |
Ресурсы |
||||||
|
Начало
5 мин
|
1.Организационный момент. Приветствие, проверка готовности учащихся к уроку 2. Актуализация знаний: 1)Что называется геометрической вероятностью? 2)В каких случаях вероятность события определяется с помощью геометрической вероятности? 3)В каких случаях вероятностьсобытия определяется с помощью классической вероятности? Устная работа: Деятельность учителя: устно опрашивает,предлагает задания по презентации. Деятельность ученика: обсуждает с другими учениками и отвечает на вопросы. Оценивание: самооценивание 1.Найти
вероятность того, что точка случайным образом брошенная в квадрат ABCD
со стороной 4 попадет в квадрат Ответ. 9/16. 2.В отрезке АВ длины 3 случайно появляется точка С. Определить вероятность того, что расстояние от точки С до В превосходит 1. Ответ: 2/3. 3.В круг радиусом 5 вписан треугольник наибольшей площади. Определите вероятность попадания в треугольник точки, случайно брошенной в круг. Ответ: |
Презентация |
||||||
|
Середина урока
10 мин
15 мин
10 мин |
2. Изучение нового материала. Цель: подведение учащихся к формулировке целеполагания урока Деятельность учителя: Предлагает учащимся решить следующую задачу: Задача №1. Рабочий контролирует работу двух независимо работающих станков.Многолетние наблюдения показали, что каждый станок (независимо друг от друга) за час работы в среднем требует 10 минут внимания рабочего.Требуется определить вероятность того,что за время, когда рабочий занят работой первого станка, потребует его внимания и второй станок. Деятельность ученика: слушают внимательно и стараются решить данную задачу. Деятельность учителя: подводит учащихся к целеполаганию урока: Итак, сегодня мы будем заниматься решением таких задач, как задачи на «встречу». Происходит знакомство с темой урока и целями обучения урока.
Объяснение учителя:
В процессе решения таких задач не сразу обнаруживается, что задачу необходимо решать геометрическим способом. Поэтому проделав полный анализ условия задачи, следует обратить внимание на следующие моменты: - множество всех возможных исходов испытания и множество благоприятствующихнам исходов принимают бесконечное множество значений (во множестве действительных чисел); - если в процессе решения задачи вводятся независимые переменные, меняющиеся во множестве действительных чисел, то способ решения задачи зависит от количества вводимых переменных:при одной переменной задача решается на числовой оси; при двух переменных задача решается на координатной плоскости и т.д.
Деятельность ученика:слушают внимательно Деятельность учителя: подводит учащихся к тому, что они с помощьювведения двух переменных составляют систему неравенств. Дает учащимся готовое решение данной задачи на листах для того, чтобы они самостоятельно разобрали решение. Деятельность ученика:работая в парах самостоятельно разбирают решение задачи№1. Деятельность учителя: консультирует учащихся,ели у них возникают вопросы. Решение:(см.Приложение 1) 3.Решение задач. 3.1.Деление на группы. Учащиеся делятся на две группы с помощью палочек синего и зеленого цвета. 3.2.Групповая работа. Деятельность учителя:каждой группе дает по одной задаче для самостоятельного решения. Деятельность ученика:учащиеся решают, предложенные задачи в группах, а затем презентуют свое решение для второй группы. I группа.Задача№2.(о встрече) Айбек и Айнур пришли в кафе между 10:00 и 12:00 часов. Они договорились о том, что они будут ждать друг друга 15 минут до того, как они уйдут. Найдите вероятность того, что они встретятся в этом кафе. II группа.Задача №3.(о встрече) Коля и Оля договорились встретиться о в Центральном парке с 12:00 до 13:00. Пришедший первым ждет другого в течение 30 минут. После чего уходит. Какова вероятность, что они встретятся? Оценивание: взаимооценивание Критерии оценивания работы групп: 1.Сплоченность 2.Аккуратность 3.Убедительность 4.Результативность. 4.Формативное оценивание. Индивидуальная работа. Цель: проверить усвоение учащимися понятия геометрической вероятности и умения применить при решении задач. (см. приложение №3) Деятельность ученика: письменно выполняют задание в тетрадях. Деятельность учителя: наблюдает за работой учащихся Оценивание: оценивание учителем. |
Шыныбеков А.Н. учебник для 9 класса (с.211-212) К
Презентация
П
Г
Приложение №3 И
|
||||||
|
Конец 5 мин |
3.Рефлексия.Подведение итогов урока. Цель:помочь ученику проанализировать свою деятельность на уроке. Учащиеся отвечают на следующие вопросы - Что узнал, чему научился? - Что осталось непонятным? - Над чем необходимо работать?
Задание на дом: (см. Приложение №4) |
Приложение №4 |
||||||
|
Дополнительная информация |
||||||||
|
Дифференциация – как Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? |
Оценивание – как Вы планируете проверить уровень усвоения материала учащихся? |
Межпредметные
связи |
||||||
|
|
|
|
||||||
|
Общая оценка Какие два аспекта урока прошли хорошо (подумайтекак о преподавании, так и об обучении)? 1: 2: Какие две вещи могли бы улучшить урок (подумайте как о преподавании, так и об обучении)? 1: 2: Что я узнал(а) за время урока о классе или отдельных учениках такого, что поможет мне подготовиться к следующему уроку? |
||||||||
.
Приложение №1.
Обозначим
через х то время .когда рабочий занят работой первого станка, а через у – время
, когда и второму необходимо уделить внимание ,Если за то время ,когда рабочий
занят работой первого станка ,необходимо уделить внимание работе и второго
станка, то должно выполняться неравенство ![]() т.
Е. имеем двойное неравенство
т.
Е. имеем двойное неравенство ![]() На первый
взгляд хотя и кажется , что сначала вышел из строя первый станок , а затем
неполадки обнаружились и во втором станке, т.е.
На первый
взгляд хотя и кажется , что сначала вышел из строя первый станок , а затем
неполадки обнаружились и во втором станке, т.е. ![]() ,cлучай
,cлучай ![]() в полной мере отвечает условиям задачи,
ибо по условиям задачи нас интересует то ,что станки потребуют внимания
рабочего в одних и тех же отрезках времени. Итак, множество всех
благоприятствующих нам точек плоскости удовлетворяют системе неравенств:
в полной мере отвечает условиям задачи,
ибо по условиям задачи нас интересует то ,что станки потребуют внимания
рабочего в одних и тех же отрезках времени. Итак, множество всех
благоприятствующих нам точек плоскости удовлетворяют системе неравенств: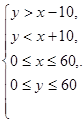
а множество всех возможных исходов определяется неравенствами. На рисунке 1 множество всевозможных исходов изображено в виде квадрата со стороной 60, а множество благоприятствующих нам исходов определяется закрашенной фигурой. Тогда по формуле имеем:
![]()
Приложение №2.
Задание 1.
Айбек и Айнур пришли в кафе между 10:00 и 12:00 часов. Они договорились о том, что они будут ждать друг-друга 15 минут до того, как они уйдут. Найдите вероятность того, что они встретятся в этом кафе.
Ответ: В этой задаче можно использовать двухмерное пространство для изображения времени двух людей:
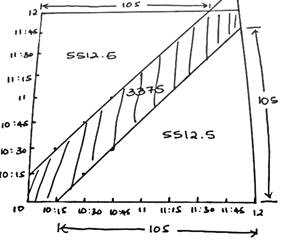
Тогда закрашенная область будет являться временем встречи Айбек и Айнур.
![]()
Ответ:![]()
Приложение №3.
Формативное оценивание
№1. Двое условились встретится в определенном месте между 17 и 18 часами. По договоренности каждый из них приходит и ждет второго ровно Tминут и в случае, если второй партнер за это время не приходит в назначенное место, он уходит. Какова вероятность встречи партнеров? Решите задачу при T=20 мин.
2. Два лица А и В договорились встретиться в определенном месте в промежутке времени от 900 до 1000. Каждый из них приходит наудачу (в указанный промежуток времени), независимо от другого и ожидает 10 минут. Какова вероятность того, что они встретятся?
Ответ. 11/36.
3. Буратино посадил на прямоугольный лист размером 20 см на 25 см круглую кляксу радиусом 1 см. Сразу после этого Буратино посадил еще одну такую же кляксу, которая целиком оказалась на листе. Найдите вероятность того, что эти две кляксы не соприкасаются.
Ответ. 0,97
Приложение №4.
Домашнее задание.
1. В окружность вписан квадрат ABCD. На этой окружности случайным образом выбирается точка М. Найдите вероятность того, что эта точка лежит на:
а) меньшей дуге АВ; б) большей дуге АВ.
Ответ. а) 1/4; б) 3/4.
2. На отрезок [3;6] случайным образом бросается точка Х. С какой вероятностью выполняется неравенство: а) ; б) ; в) ?
Ответ. а) 1/3; б) 1/3; в) 1/3.
3. Про село Иваново известно только, что оно находится где-то на шоссе между Миргородом и Старгородом. Длина шоссе равна 200 км. Найдите вероятность того, что:
а) от Миргорода до Иваново по шоссе меньше 20 км;
б) от Старгорода до Иваново по шоссе больше 130 км;
в) Иваново находится менее чем в 5 км от середины пути между городами.
Ответ. а) 0,1; б) 0,35; в) 0,05.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.