1Нелинейные уравнения с двумя переменными и их системы_ Теоретический материал

Решение текстовых задач с помощью систем уравнений

Алгоритм решения текстовых задач с помощью систем уравнений:

• Составление математической модели.
• Решение математической модели.
• Вывод ответа на вопрос задачи.

Математической моделью называется представление реальной ситуации с помощью математического языка.

Для составления математической модели следует:

1. Определить постановку вопроса задачи, то есть определить неизвестные данные, значения которых необходимо найти.
2. Определить известные исходные данные.
3. Определить свойства и принципы, которые устанавливают зависимость между неизвестными и известными данными.
4. Построить уравнения, отражающие свойства и принципы зависимости между неизвестными и известными данными.
5. Проверить выполнение уравнений.

Например, в работе над макетом научного проекта Аина вырезала из большего квадрата квадрат меньшего размера, сторона которого составляет   стороны большого квадрата, и общая площадь остатков отреза составила 245 см². Определим размеры большого и вырезанного квадратов. Пусть x – сторона большого квадрата и y – сторона квадрата, вырезанного Аиной. Из условия следует, что x составляет . Так как площади большого и вырезанного квадратов равны соответственно x² и y², то их разность есть x² – y² = 245см². Таким образом, мы получили систему уравнений:

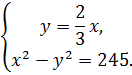
Решим данную систему уравнений методом подстановки. Подставим во второе уравнение значение из первого уравнения:

x² – = 245,

и упростим его:

x² = 441.

Решениями последнего уравнения являются x₁ = 21 и x₂ = –21. В силу того, что сторона квадрата может принимать только положительные значения, x₂ = –21 не соответствует условию задачи, значит, сторона большого квадрата составляет 21 см. Для определения стороны квадрата, вырезанного Аиной, подставим значение x = 21 в первое уравнение системы уравнений:

x = ⋅ 21 = 14 см,

то есть сторона квадрата, вырезанного Аиной составляет 14 см.

Источник:

https://bilimland.kz/ru/subject/algebra/9-klass/reshenie-tekstovyx-zadach-s-pomoshyu-sistem-uravnenij