Добавить материал

и получить 10 документов
и свидетельство автора

Изображение пользователя Рыбинок Екатерина Валерьевна Рыбинок Екатерина Валерьевна

1Ссоч 9 кл

  • docx
  • 25.04.2020
Публикация на сайте для учителей

Публикация педагогических разработок

Бесплатное участие. Свидетельство автора сразу.
Мгновенные 10 документов в портфолио.

Добавить материал
Иконка файла материала 1Ссоч 9 кл.docx

СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ

Обзор суммативного оценивания за 1 четверть

 

Продолжительность 40 минут Количество баллов–30 баллов

 

Типы заданий:

МВО–задания с множественным выбором ответов;

КО–задания, требующие краткого ответа;

РО–задания, требующие развернутого ответа.

 

Структура суммативного оценивания

 

Данный вариант состоит из 11 заданий, включающих задания с множественным выбором ответов, с кратким и развернутым ответами.

В вопросах с множественным выбором ответов обучающийся выбирает правильный ответ из предложенных вариантов ответов.

В заданиях, требующих краткого ответа, обучающийся записывает ответ виде численного значения, слова или короткого предложения.

В заданиях, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.

 

Характеристика заданий суммативного оценивания за 1 четверть

 

 

Раздел

Проверяемая цель

Уровень мыслительных навыков

Кол. заданий*

№ задания*

Тип задания*

Время на выполнение, мин*

Балл*

Балл за раздел

Основы кинематики

9.2.1.4 - находить перемещение, скорость и ускорение из графиков зависимости этих величин от времени

Применение

9

1

8

10

МВО

КО

РО

1

55

1

7

3

25

9.2.1.6 - применять уравнения координаты и перемещения при равнопеременном прямолинейном движении в решении задач

Применение

2

3

9

МВО

МВО

РО

1

1

6

1

2

3

9.2.1.7 - экспериментально определять ускорение тела при равноускоренном движении

Навыки высокого порядка

7

РО

5

3

9.2.1.14 - применять формулу взаимосвязи линейной  и угловой скорости при решении задач

Применение

6

РО

4

3

9.2.1.15 - применять формулы центростремительного ускорения при решении задач

Применение

5

КО

4

2

Основы астрономии

9.7.2.4 – определять небесные координаты звезд по подвижной карте звездного неба

Применение

2

11

КО

4

2

5

9.7.2.7 - объяснять движение небесных тел на основе законов Кеплера

Знание и понимание

4

КО

1

1

9.7.2.8 - объяснять использование метода параллакса для определения расстояний или размеров тел в солнечной системе

Применение

 

РО

3

2

 

Итого:

 

11

 

 

40

30

30

Примечание:*-разделы,вкоторыеможновноситьизменения

Задания суммативного оценивания за 1 четверть по предмету «Физика»

 

1. Человек последовательно прошел на север 3 км, на восток 4 км. Чему равен модуль перемещения?

А) 7 км              В) 3 км           С) 5 км             D) 1 км                Е) 4 км                                [1]

 

2. Скорость автомобиля за 20с уменьшилась с 20м/с до 10м/с. С каким средним ускорением двигался автомобиль?

А) 0,5м/с2          B) 5м/с2          C) -5м/с2          D) -0,5м/с2          E) 50 м/с2                              [1]

 

3. Выберите какая из формул соответствуют ускорению.

А) (υ - υ0) / t

B)  4π2R

C) υo + at

D) υ2/ R

E) S/ t

F) υ0t + at2/2

G) ѡ2/R                                                                                                                                     [2]

 

4. Заполните таблицу:                                                                                                                           [3]

 

Понятие

Определение

Объяснение нахождение расстояние до небесного тела (только для горизонтального параллакса)

Афелий

 

 

Горизонтальный параллакс

 

 

 

5. Радиус-вектор 6м задающий положение лошади, движущейся по окружности на арене цирка, повернулся на угол  промежуток времени  4 с. Определите угловую скорость движения лошади и его центростремительное ускорение.                                                                           [2]

 

 

6. Барабан стиральной машины при отжиме белья вращается равномерно с частотой = 400 Диаметр барабана d = 40 см. Определите модуль линейной скорости точек на поверхности барабана и период вращения барабана.                                                                                         [3]

 

 

7. При эксперименте были измерены следующие значения:

№ опыта

t, с

S, м

а, м/с2

1

6

0,5

 

2

5,5

 

0,033

3

 

0,49

0,039


1) вычислите ускорение шарика при равноускоренном движении.                                           [1]

 

2) Вычислите значение перемещения шарика.                                                                             [1]

 

3) Вычислите время движения шарика.                                                                                         [1]

 

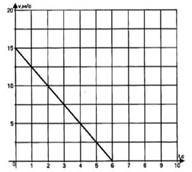https://uchitel.pro/wp-content/uploads/2018/10/2018-10-06_21-04-21-300x223.jpg8. График показывает зависимость скорости от времени. По графику проекции скорости определите:

 

1) начальную скорость тела;                                                       [1]

 

2) время движения тела до остановки;                                       [1]

 

3) ускорение тела;                                                                         [1]

 

4) вид движения (разгоняется тело или тормозит), почему?   [2]

 

5) запишите уравнение проекции скорости;                                                                                 [1]

 

6) запишите уравнение координаты (начальную координату считайте равной нулю).           [1]

 

9. Из начальной точки с координатами х0 = -3 м и у0 = 1 м тело прошло некоторый путь, так что проекция вектора перемещения на ось х оказалась равной 5,2 м, а на ось у-3 м. Найдите координаты конечного положения тела. Начертите вектор перемещения.                               [3]

 

 

10. Отрезав дно цистерны заполнили ее водой. Высота столба воды в нём уменьшается по закону  .Постройте график этой функции.                                                       [3]

 

 

 

 

 

 

 

 

 

 

 

 

 


11.  С помощью подвижной карты звездного неба определите небесные координаты звезд.     [2]

 

Название звезды

Координаты звезды

α Большой Медведицы

 

 

 

 

Схема выставления баллов

Вопрос

Ответ

Балл

Дополнительная информация

1

С

1

 

2

D

1

 

3

A

1

 

D

1

 

4

1)      Угол, под которым с небесного тела виден радиус Земли, перпендикулярный к лучу зрения, называют горизонтальным параллаксом.

2)      Если углы Qи ρ малы, то синусы пропорциональны углам, и можно написать:

Этот способ определения размеров светил применим только тогда, когда виден диск светила

3)      Афелий- самая удаленная точка от солнце.

1

 

 

 

1

 

 

 

 

 

 

1

 

5

ѡ = 1,18 рад/с

а = 8,35 м/с2

1

1

 

6

T = 0,15 c;

Использует формулу взаимосвязи линейной и угловой скорости; R = d/2;

υ = 8,4м/с

1

1

 

1

ᴠ =

7

0,028 м/с2,

0,5 м,

5 с

1

1

1

 

8

1)      ʋ0x = 15 м/с

2)      t = 6 c

3)      ax = - 2,5 м/с2

4)      тело тормозит,

так как скорость его уменьшается

5)      ʋx = 15 - 2,5t

6)      x(t) = 15t - 1,25t2

1

1

1

1

1

1

1

 

9

x = 2,2 м;

 y = 4 м;

|| ≈ 6 м

1

1

1

 

10

Вычисляет значения переменной y при заданном значении;

Указывает оси координат

Строит график

1

 

1

1

 

11

α1 = 22ч55м,

δ1 = -30°.

1

1

 

 

 

СПЕЦИФИКАЦИЯ СУММАТИ ВНОГО ОЦЕНИ Хара к т е р исти к а зад а н и й сумматив н ого оц е н и ва н ия за 1… За д а ни я с умм а т ив н о г о оценива ни я за 1 четверть п о п р едме… График показывает зависимость скорости от времени Схема выставления баллов

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также