Методические рекомендации к уроку

Тема урока "Числовые неравенства и их свойства"

Цели обучения:

6.2.2.5

знать и применять свойства верных числовых неравенств;

6.2.2.6

понимать и применять сложение, вычитание, умножение и деление неравенств

Критерии оценивания

Учащийся:

знает:

·         определение числового неравенства;

·         свойства числовых неравенств;

·         понятие о верных и неверных числовых неравенствах;

·         правила сравнения  и свойства числовых неравенств;

·         как выполнять действия над числовыми неравенствами, применяя их свойства.

умеет:

·         сравнивать выражения на основе правила сравнения;

·         применять свойства числовых неравенств  на практике, при оценке значений выражений;

·         выполнять действия с неравенствами на основе правил сложения и умножения числовых неравенств;

·         выполнять действия над числовыми неравенствами, применяя их свойства.

Теоретический материал

Числовое неравенство – это неравенство, в записи которого по обе стороны от знака неравенства находятся числа или числовые выражения, неравенство называется числовым, если каждая из его частей является числовым выражением.

Неравенство может быть верным (если представляет собой истину) или неверным.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Решить задания на повторение.

Приложение 1.

Проверка по готовым ключам. Сделать предварительные выводы.

Числовые неравенства - основной вопрос, который стоит на сегодняшнем уроке.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Работа с классом. Ввод в тему урока, используя основные знания и навыки сравнения чисел:  Действия с неравенствами.

1) Неравенства одинакового знака можно почленно складывать.
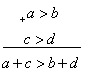 или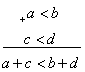

2) Неравенства противоположных знаков можно почленно вычитать, оставляя знак того неравенства, из которого производится вычитание.
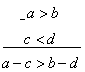 или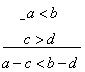

3) Неравенства одинаковых знаков с положительными членами можно почленно умножать.

С учащимися разобрать примеры применения правил действия с неравенствами.

1) При почленном сложении неравенств одного и того же смысла, образуется неравенство того же смысла
  6 < a < 8
10 < b < 12
16 < a + b < 20
2) Если из одного неравенства вычесть почленно  другое неравенство противоположного смысла, то образуется неравенство того же смысла, что и первое
  6 < a < 8
12 > b > 10
-6 < a - b < -2
3) При почленном перемножении двух неравенств одного смысла получается неравенство того же смысла

60 < a · b < 96

4) Неравенство а > b и неравенство 1/а < 1/b имеют противоположный смысл рассмотрим 10 < b < 12 и получим из него >>

Перемножим неравенства   и  >>  получим    или

0,8 >  > 0,5

Таким образом можно производить действие деление.

5) Оцените площадь прямоугольника со сторонами  и , если и

, тогда:

16,1219,47

Первичное закрепление. Практическое применение темы. При выполнении задания можно использовать прием «Активный класс». Пригласите к доске 3 учащихся попросите их записать подробное решение 1-3 соответственно. Учащиеся на местах решают все примеры и сверяют свои решения с записями на доске. С целью развития математической речи попросите одного из учащихся подробно прокомментировать решение любого примера.

Учащиеся решают, показывая подробное решение на доске.

Для учащихся с более высокой скоростью решения организуйте "уголок Знайки", куда они

могли бы подходить и проверять свое решение или читать идею решения. Это позволяет не отвлекаться на объяснение задания, а работать в это время с остальной частью класса.

Приложение 2

2) Докажите, что если 0 < a < 7 и 0 < b < 3, то

Доказательство:

Так как 68 < 70, то 0 < 5а + 11b < 70.

.

Так как 25 < 30, то 4 < ab + 4 < 30.

3) Пусть  - основание,  - боковая сторона равнобедренного треугольника (треугольник, у которого 2 стороны равны (, а третья отлична от них (), тогда  - периметр этого треугольника.

Известно, что  

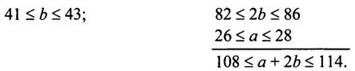
Ответ: .

4) Для библиотеки требуется комната площадью не менее 40 м² (то есть S ≥ 40).  Определите: подойдёт ли выделенное помещение для библиотеки, если ее длина , а ширина .

Если   и  – длина и ширина прямоугольной комнаты, тогда её площадь равна .

7,5 ≤ а ≤ 7,6

5,4 ≤ b ≤ 5,5   

40,5 ≤ а · b ≤ 41,8.

Так как требуется комната площадью не менее 40 м² (то есть S ≥ 40), то данное помещение подойдёт для библиотеки.

О т в е т: да.

Перейти к самостоятельной работе учащихся.

Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями.

Приложение 3

1) На координатной оси отмечены числа x, 2 и y. Укажите верное неравенство.

А) 2 – y > 0                Б) x – 2 > 0                В) x – y < 0                Г) 2 – x < 0

2) Если a < b, то

А) a + 4 > b + 4;   a –  7 > b – 7

Б) a + 4 < b + 4;    a – 7 < b – 7

В) a + 4 < b + 4;    a –  7 > b – 7

Г) a + 4 < b + 4;    a –  7 > b – 7

3) Если - 0,2 m  ³ - 0,2 n, то

А)  m £ n;                   Б)  m > n                    В)  m ³ n                    Г)  m < n

4) Какое из следующих неравенств не следует из неравенства a – b < c?

А) a – c < b                 Б) a – b – c < 0           В) b – a + c < 0           Г) a < b + c

5) Если сторона квадрата  такова, что 3 , то какое наибольшее целое значение примет его периметр.

А) 3,4                         Б) 12                           В) 13                           Г)   4

6) Известно, что а > b. Сравните:  а) 21а и 21b; б) -3,2а и -3,2b;  в) а + 8 и b + 8.

7) Известно, что а < b. Сравните:  а) 18а и 18b;  б) -6,7а и -6,7b; в) а + 5 и b + 5.

8) Зная, что 7,2 < а < 8,4 и 2 < b < 2,5, оцените:  а)  ab;     б) -2a + b;           в) .

9) Оцените периметр и площадь прямоугольника со сторонами  см и  см, если известно, что  и .

Дополнительно

Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям.

Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить учащимся задания подобные заданиям Приложения 4. Каждый выполняет самостоятельно.

Приложение 4

1. Известно, что а > b.

Сравните:  а) 21а и 21b;    б) -3,2а и -3,2b;    в) а + 8 и b + 8.

2. Сложите почленно неравенства:

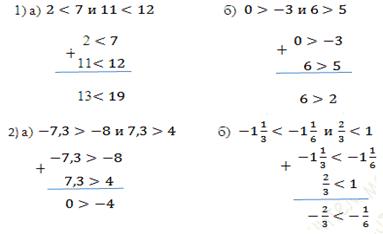
3. Перемножьте почленно неравенства: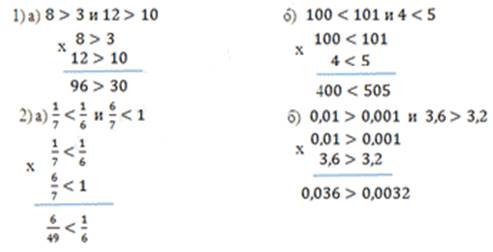

4) В результате измерения ширины x и длины y прямоугольника было установлено, что

2,5 см < x < 2,7 см и 4,1 см < y < 4,3 см. Тогда можно оценить площадь прямоугольника. Имеем:

2,5 см < x < 2,7 см
х
4,1 см < y < 4,3 см
10,25 см² < xy < 11,61 см².

После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать один из вариантов.

Беседа. Рефлексия.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1.      "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2.      "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4.      Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.